Introducción a las funciones logarítmicas

 

Objetivos de aprendizaje

·         Convertir ecuaciones logarítmicas a ecuaciones exponenciales.

·         Convertir ecuaciones exponenciales a ecuaciones logarítmicas.

·         Graficar funciones logarítmicas.

·         Resolver ecuaciones logarítmicas.

 

Introducción

 

Una familia útil de las funciones que se relacionan con las funciones exponenciales son las funciones logarítmicas. Has estado calculando el resultado de bx y esto te daba funciones exponenciales. Un logaritmo es un cálculo del exponente en la ecuación y = bx. Puesto de otro modo, encontrar un logaritmo es lo mismo que encontrar el exponente cuya base debe elevarse para obtener el valor deseado. El exponente se convierte en la salida en lugar de la entrada.

 

Calculando exponentes

 

Considera estas tablas de valores usando la base 2.

 

Tabla 1

Tabla 2

Entrada x, un exponente

Salida y

Entrada x, un número que es una potencia de 2.

Salida y, el exponente de 2.

x

y = 2x

x = 2y

y

−3

−3

−2

−2

−1

−1

0

1

1

0

1

2

2

1

2

4

4

2

3

8

8

3

 

Observa que las dos tablas son iguales excepto que las columnas están invertidas — el punto (1, 2) tomad de la primera tabla será el punto (2, 1) en la segunda tabla.

 

Las gráficas de estas dos relaciones deben tener en general la misma forma. Como se muestra en la gráfica, las dos curvas son simétricas en la línea y = x. Otra manera de decirlo, si rotas la curva roja sobre la línea y = x, va a coincidir con la curva azul. (Esto tiene sentido, porque y en la primera tabla se vuelve x en la segunda tabla y viceversa.)

 

 

La ecuación x = 2y normalmente se escribe como una función logarítmica (también llamada función log). La función logarítmica de x = 2y se escribe como y = log2 x o f(x) = log2 x. El número 2 se sigue llamando base. En general y = logb x se lee como, “y igual al logaritmo base b de x.” Al igual que con las funciones exponenciales, b > 0 y b ≠ 1.

 

 

Puedes ver en la gráfica que el rango (valores de y) de la función exponencial (en rojo) es todos los números reales positivos. Como la entrada y la salida se han cambiado, el dominio (valores de x) de la función logarítmica (en azul) es todos los números reales positivos.

 

De manera similar, el dominio de la función exponencial (en rojo) es todos los números reales. El rango de la función logarítmica (en azul) es todos los números reales.

 

 

Definición de logaritmo

 

El logaritmo de x con la base b se escribe logb x y se define como:

 

logb x = y si y sólo si by = x, donde x > 0 y b > 0, b ≠ 1.

 

 

 

Conectando ecuaciones exponenciales y logarítmicas

 

¡Es importante recordar que el resultado de un logaritmo es el exponente! Esto es, logb x pide, “¿Qué exponente con la base b dará el resultado x?”

 

 

Algunas veces, necesitarás convertir logb x = y a by = x. Otras veces, vas a convertir by = x a logb x = y. Los ejemplos en la siguiente tabla muestran algunas ecuaciones en formas logarítmicas y su correspondiente forma exponencial.

 

Forma logarítmica

Forma exponencial

log2 16 = 4

24 = 16

log7 1 = 0

70 = 1

log5 5 = 1

51 = 5

4-1 =

10-2 = 0.01

 

Conocer esta conexión es esencial para entender y trabajar con logaritmos.

 

 

Ejemplo

Problema

Reescribir log3 9 = 2 como una ecuación exponencial.

 

 

 

 

 

 

 

 

 

Necesitas cambiar

a la forma by = x.

 

 

Aquí la base es 3 y el exponente es 2.

 

 

Sustituye b y y x en la ecuación exponencial, by = x.

 

Respuesta

                                           32 = 9

Comprueba el resultado: ¿Es 32 igual a? ¡Sí!

 

 

Si bien la entrada de un logaritmos siempre debe ser positiva, el resultado (¡un exponente!) puede ser negativo.

 

 

Ejemplo

Problema

Convertir log4 = −2 a una ecuación exponencial.

 

 

 

 

 

 

Necesitas reescribir   en la forma by = x.

 

 

Aquí la base es 4 y el exponente es −2.

 

 

Sustituye b y y x en la ecuación exponencial, by = x.

 

Respuesta

Comprueba el resultado:

 

 

Convertir  a una ecuación exponencial.

 

A)

B)

C)

D)

Mostrar/Ocultar Respuesta

A)

Incorrecto. El exponente es negativo, no positivo. La respuesta correcta es .

 

B)

Incorrecto. Si bien este enunciado es válido, la base en la respuesta es 81, mientras que la base en la ecuación logarítmica original es 3. La respuesta correcta es .

 

C)

Correcto. La base es 3 y el exponente es −4, so.

 

D)

Incorrecto. Si bien este es un enunciado válido, el exponente en la ecuación logarítmica original es -4, no 4. La respuesta correcta es .

 

 

 

Como hemos visto, es posible convertir ecuaciones logarítmicas a ecuaciones exponenciales. También es posible convertir ecuaciones exponenciales a ecuaciones logarítmicas.

 

 

Ejemplo

Problema

Reescribir 53 = 125 como una ecuación logarítmica.

 

 

 

 

 

 

Necesitas reescribir en la forma logb x = y.

 

 

Aquí la base es 5 y el exponente es 3.

 

 

 

 

Sustituye por b, y y x en la ecuación logarítmica,

.

 

Respuesta

log5 125 = 3

 

 

Ejemplo

Problema

Convertir 10-3 =  en una ecuación logarítmica.

 

 

 

 

 

 

 

 

Necesitas reescribiren la forma logb  x = y.

 

 

 

Aquí la base es 10 y el exponente es −3.

 

 

 

 

 

Sustituye por b, y y x en la ecuación logarítmica,

.

 

 

Respuesta

 

 

 

Recuerda que las raíces también son exponentes.

 

 

Ejemplo

Problema

Convertir  en una ecuación logarítmica.

 

 

 

 

Reescribe la raíz cuadrada usando un exponente fraccional. Necesitas reescribir en la forma logb  x = y.

 

 

 

 

 

 

 

 

 

Aquí la base es 49 y el exponente es 

 

 

 

Sustituye por b, y y x en la ecuación logarítmica, .

 

Respuesta

log49 7 =

 

 

 

Convertir 112 = 121 en una ecuación logarítmica.

 

A)

B)

C)

D)

 

Mostrar/Ocultar Respuesta

A)

Incorrecto. Encontrar un logaritmo es lo mismo que encontrar el exponente al que la base dada debe elevarse para obtener el valor deseado, entonces 2 debe quedar solo a un lado de la ecuación. La respuesta correcta es .

 

B)

Incorrecto. La base de la ecuación exponencial, 11, también es la base (el número pequeño al final de “log”) en la ecuación logarítmica. La respuesta correcta es .

 

C)

Correcto. La base es 11 y el resultado del logaritmo, 2, es el exponente.

 

D)

Incorrecto. La base de la ecuación exponencial, 11, es también la base (el número pequeño al final de “log”) en la ecuación logarítmica. La respuesta correcta es .

 

 

 

Graficando funciones logarítmicas

 

Observa la siguiente gráfica. Muestra algo familiar — ¡la vista al inicio de este tema! La gráfica azul es la función logarítmica y la gráfica roja es la función exponencial correspondiente.

 

 

Cuando graficamos funciones logarítmicas, es importante recordar lo siguiente:

 

·         La gráfica sólo puede aparecer a la derecha del eje y. Esto es porque el domino está restringido a los valores positivos de x.

·         La gráfica se acerca al eje y para valores pequeños de x (cerca de x = 0).

 

Recuerda que las funciones logarítmicas casi se comportan como funciones exponenciales. Sólo tienes que cambiar los valores de x por los de y. Por ejemplo, el segundo enunciado de arriba es como la función exponencial acercándose al eje x (cerda de y = 0).

 

 

Ejemplo

Problema

Graficar f(x) = log3 x.

 

 

Grafica y = log3 x.

 

Esto es lo mismo que 3y = x.

Para hacer los cálculos más fáciles, primero convierte esto a una ecuación logarítmica en y. Luego convierte el logaritmo a una ecuación exponencial.

 

x = 3y

y

 

−2

 

−1

 

0

 

1

 

2

Empieza con una tabla de valores.

 

Con las funciones logarítmicas, es normalmente más fácil escoger los valores de y en lugar de los valores de x. Asegúrate de incluir algunos valores negativos para y.

 

x = 3y

y

−2

−1

1

0

3

1

9

2

¡Ten cuidado con los exponentes negativos!

 

Usa la tabla como pares ordenados. Recuerda que la gráfica de la función mostrará todas las correspondencias entre x y y, por lo que cualquier par que pueda estar en la tabla debe ir en la gráfica.

 

 

 

 

 

Grafíca los puntos.

Respuesta

Como los puntos no forman una línea, no puedes usar una regla. Conecta los puntos lo mejor que puedas, usando una curva suave (no una serie de líneas rectas).

 

Recuerda que las funciones logarítmicas se acercan al eje y (pero nunca lo tocan ni lo cruzan).

 

 

Ejemplo

Problema

Graficar f(x) = log4 x.

 

 

Grafica y = log4x.

 

Esto es lo mismo que 4y = x.

Para hacer los cálculos más fáciles, primero convierte esto a una ecuación logarítmica en y. Luego convierte el logaritmo a una ecuación exponencial.

 

x = 4y

y

−2

−1

1

0

4

1

16

2

Empieza con una tabla de valores, escogiendo los valores de y calculando x.

 

¡Ten cuidado con los exponentes negativos!

 

 

 

Usa la tabla como pares ordenados y grafica los puntos.

 

En este caso, (16, 2) no aparecerá en la gráfica. Porque conoces la raíz cuadrada de 4, intenta x =. En este caso, sería. Ese punto aparece en azul.

Respuesta

Como los puntos no forman una línea, no puedes usar una regla. Conecta los puntos lo mejor que puedas, usando una curva suave (no una serie de líneas rectas).

 

Recuerda que las funciones logarítmicas se acercan al eje y (pero nunca lo tocan ni lo cruzan).

 

 

Vamos a comparar las gráficas logarítmicas que has visto: f(x) = log2 x, f(x) = log3 x y f(x) = log4 x.

 

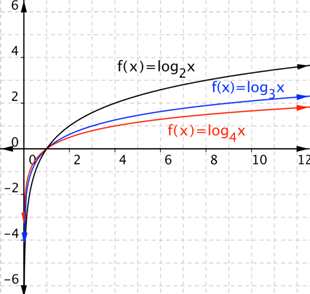
Observa que una base más grande hace la gráfica menos inclinada. (Esto es lo opuesto que con las funciones exponenciales, donde una base más grande significa una gráfica más inclinada). Una base más grande también hace que la gráfica se acerque al eje x por y > 0 (o x > 1) y más cerca del eje y por y < 0 (o x < 1). Todas las gráficas pasan por (1, 0), mientras que todas las funciones exponenciales siempre pasan por (0, 1).

 

Con las funciones exponenciales, las gráficas aumentaban (crecimiento exponencial) cuando la base b era mayor que 1. Y decrecían (decaimiento exponencial) cuando la base b era menor que 1. Las gráficas logarítmicas de arriba aumentan y todas tienen una base mayor que 1. Veamos lo que pasa cuando la base es menor que 1.

 

 

Ejemplo

Problema

Graficar .

 

 

Escribe una ecuación exponencial en y para ayudarte.

 

x

y

16

−2

4

−1

1

0

1

2

Crea una tabla de valores, De nuevo, recuerda tener cuidado con los exponentes negativos. Recuerda sacar el recíproco de la base para tener un exponente positivo..

 

Observa que en esta tabla, los valores de x disminuyen y los valores de y aumentan.

 

 

Usa los pares de la tabla para graficar los puntos. Podrías incluir puntos nuevos, especialmente cuando uno de los puntos de la tabla no cabe en tu gráfica. (16,−2) se sale de la gráfica. Como conoces la raíz cuadrada de 4, intenta x =:

El punto (8,) ha sido incluido en azul. Podría no ser necesario incluir puntos adicionales. También podrías requerir de una calculadora, dependiendo de la base.

Respuesta

Conecta los puntos lo mejor que puedas, usando una curva suave.

 

 

Si la base es menor que 1, la función logarítmica va a decrecer. La gráfica se acerca al eje y cuando x es pequeña, pero con valores de y positivos en lugar de negativos.

 

 

¿Cuál de las siguientes gráficas representa f(x) = ?

 

A)

B)

C)

D)

 

Mostrar/Ocultar Respuesta

A)

 

Incorrecto. Esta gráfica aumenta porque los valores de f(x) aumentan conforme x aumenta. (Compara los valores con x = 1 y x = 2.) Esta es la gráfica de f(x) = log3 x. La respuesta correcta es la Gráfica D.

 

B)

 

Incorrecto. Esta función tiene un dominio con todos los números reales y un rango de todos los números reales positivos. Las funciones logarítmicas tienen dominios con todos los números reales positivos y rangos con todos los números reales. La respuesta correcta es la Gráfica D.

 

C)

 

Incorrecto. Esta gráfica disminuye, pero tiene un dominio con todos los números reales y un rango con todos los números reales positivos. Las funciones logarítmicas tienen dominios con todos los números reales positivos y rangos con todos los números reales. La respuesta correcta es la Gráfica D.

 

D)

 

Correcto. La base es menor que 1, por lo que la gráfica muestra una función decreciente. El dominio es todos los números reales positivos y el rango es todos los números reales.

 

 

 

Resolviendo ecuaciones logarítmicas

 

Como has visto, hay tres cantidades esenciales en una ecuación logarítmica y = logb x: la base b, el exponente y y la entrada x. Cualquiera de ellos podría faltar en una ecuación que debes resolver. Normalmente la manera más fácil de resolver esto es convirtiendo la ecuación logarítmica a una ecuación exponencial.

 

Ejemplo

Problema

Resolver 4 = log5 x.

 

 

4 = log5 x es lo mismo que 54 = x.

Convierte la ecuación logarítmica a una ecuación exponencial.

 

54 = 5 • 5 • 5 • 5

54 = 25 • 25

54 = 625

En este caso, sólo necesitas evaluar  para resolver x.

Respuesta

x = 625

 

 

 

Cuando resuelves b o y, es útil tener en tu mente presentes muchas relaciones exponenciales, como 53 = 125 y 25 = 32. Sin embargo, aunque no las tengas, puedes pensar un poco para aproximar o incluso encontrar soluciones exactas.

 

 

Ejemplo

Problema

Resolver 3 = logb 64.

 

 

3 = logb 64 es lo mismo que b3 = 64.

Convierte la ecuación logarítmica a una ecuación exponencial.

 

 

Podrías no saber qué número elevado a la tercera potencia es 64. Puedes intentar rápidamente con algunos.

 

13 = 1

103 = 1,000

13 y 103 son fáciles de calcular, por lo que empezamos con ellos.

 

64 se acerca más a 1 que a 1,000, entonces la base correcta se acercará más a 1 que a 10.

 

 

Intentemos otros valores. Como 64 es par, sabes que no necesitas intentar con números impares. Un número impar a cualquier potencia resulta en un número impar. Y un número par a cualquier potencia resulta en un número par

 

23 = 8

43 = 4 • 16 = 64

Entonces intenta con 2 y con 4.

Respuesta

b = 4

¡Lo encontraste! Asegúrate de que usas el número correcto para tu respuesta. ¡Podría ser fácil responder erróneamente “64”!

 

 

Intentemos otro:

 

 

Ejemplo

Problema

Resolver y = log5 125.

 

 

y = log5 125 es lo mismo que 5y = 125.

Convierte la ecuación logarítmica a una ecuación exponencial.

 

y

5y

1

5

2

25

3

125

¿Qué potencia de 5 es 125? Podrías saber, pero si no, has una tabla de valores de y y 5y. Busca el 125 o algo cerca, en la columna 5y.

Respuesta

y = 3

De nuevo, asegúrate de que usas el número correcto para tu respuesta. ¡Podría ser fácil responder erróneamente “125”!

 

 

Resolver 4 = log2 x para x.

 

A)

B) 2

C) 8

D) 16

 

Mostrar/Ocultar Respuesta

A)

Incorrecto. El equivalente de la ecuación exponencial es 24 = x. Pudiste haber escrito incorrectamente 4x = 2. La respuesta correcta es 16.

 

B) 2

Incorrecto. El equivalente de la ecuación exponencial es 24 = x. Pudiste haber escrito incorrectamente 2x = 4. La respuesta correcta es 16.

 

C) 8

Incorrecto. El equivalente de la ecuación exponencial es 24 = x. La respuesta correcta es 16.

 

D) 16

Correcto. El equivalente de la ecuación exponencial es 24 = x, que es 16.

 

 

 

Sumario

Las funciones logarítmicas se parecen a las ecuaciones exponenciales. De hecho, logb x = y representa lo mismo que by = x. Las gráficas se parecen, pero con características cambiadas como el dominio y el rango entre los valores de x y los valores de y. Convertir una ecuación logarítmica a su ecuación exponencial equivalente puede ser útil para graficar y resolver ecuaciones.