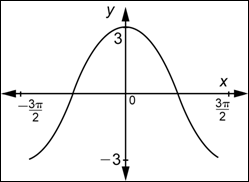
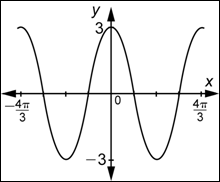
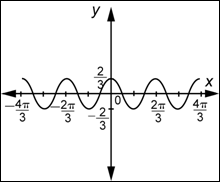
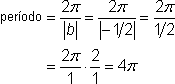Amplitud y Periodo
Objetivos de Aprendizaje
· Entender la amplitud y el periodo.
· Graficar la función seno con cambios en la amplitud y el periodo.
· Graficar la función coseno con cambios en la amplitud y el periodo.
· Corresponder una función seno o coseno con su gráfica y vice versa.
Introducción
Sabes como graficar las funciones ![]() y
y ![]() . Ahora aprenderás cómo graficar toda la “familia” de las funciones seno y coseno. Estas funciones tienen la forma
. Ahora aprenderás cómo graficar toda la “familia” de las funciones seno y coseno. Estas funciones tienen la forma ![]() o
o ![]() , donde a y b son constantes.
, donde a y b son constantes.
Anteriormente, usamos la variable ![]() para mostrar un ángulo en la posición estándar, y también nos referimos a las funciones seno y coseno como
para mostrar un ángulo en la posición estándar, y también nos referimos a las funciones seno y coseno como ![]() y
y ![]() . Normalmente las funciones seno y coseno se usan en aplicaciones que no tienen nada que ver con triángulos o ángulos, y la letra x se usa en lugar de
. Normalmente las funciones seno y coseno se usan en aplicaciones que no tienen nada que ver con triángulos o ángulos, y la letra x se usa en lugar de ![]() para la entrada (así como para etiquetar el eje horizontal). Entonces, de hoy en adelante, nos referiremos a las mismas funciones como
para la entrada (así como para etiquetar el eje horizontal). Entonces, de hoy en adelante, nos referiremos a las mismas funciones como ![]() y
y ![]() . Este cambio no afecta las gráficas.
. Este cambio no afecta las gráficas.
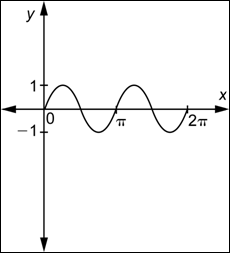
Sabes que las gráficas de las funciones seno y coseno tienen un patrón de lomas y valles que se repiten. La longitud de éste patrón es ![]() . Esto es, la gráfica de
. Esto es, la gráfica de ![]() ( o
( o ![]() ) en el intervalo
) en el intervalo ![]() se parece a la gráfica en el intervalo
se parece a la gráfica en el intervalo ![]() o
o ![]() o
o ![]() . El patrón continúa infinitamente en ambas direcciones.
. El patrón continúa infinitamente en ambas direcciones.
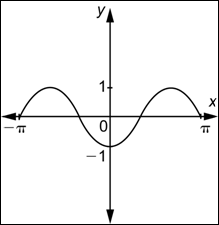
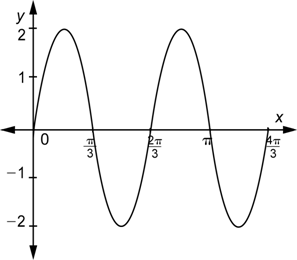
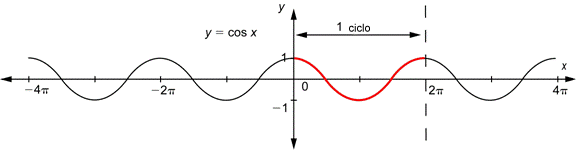
La gráfica siguiente muestra cuatro repeticiones del patrón de longitud ![]() . Cada una contiene exactamente una copia completa del patrón “loma y valle”.
. Cada una contiene exactamente una copia completa del patrón “loma y valle”.
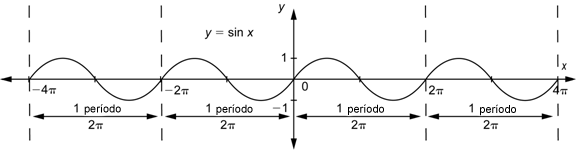
Si una función tiene un patrón repetitivo como el seno o el coseno, se llama función periódica. El periodo es la longitud del intervalo más pequeño que contiene exactamente una copia del patrón repetido. Entonces el periodo de ![]() o
o ![]() es
es ![]() . Cualquier parte de la gráfica que muestre éste patrón sobre un periodo se llama ciclo. Por ejemplo, la gráfica de
. Cualquier parte de la gráfica que muestre éste patrón sobre un periodo se llama ciclo. Por ejemplo, la gráfica de ![]() en el intervalo
en el intervalo ![]() es un ciclo.
es un ciclo.
Sabes que de graficar funciones cuadráticas de la forma ![]() que conforme cambias el valor de a cambias el “ancho” de la gráfica. Ahora estudiaremos las funciones de la forma
que conforme cambias el valor de a cambias el “ancho” de la gráfica. Ahora estudiaremos las funciones de la forma ![]() y veremos cómo los cambios en b afectan la gráfica. Por ejemplo, ¿es
y veremos cómo los cambios en b afectan la gráfica. Por ejemplo, ¿es ![]() periódica?, y si lo es, ¿cuál es el periodo? Aquí hay una tabla con algunas entradas y salidas para ésta función.
periódica?, y si lo es, ¿cuál es el periodo? Aquí hay una tabla con algunas entradas y salidas para ésta función.
| x (en radianes) | 2x (en radianes) | sen2x |
| 0 | 0 | 0 |
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
| 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0 |
Conforme los valores de x van de 0 a ![]() , los valores de
, los valores de ![]() van de 0 a
van de 0 a ![]() . Podemos ver de la gráfica que la función
. Podemos ver de la gráfica que la función ![]() es una función periódica, y va por un ciclo completo en el intervalo [0,
es una función periódica, y va por un ciclo completo en el intervalo [0, ![]() ], entonces su periodo es
], entonces su periodo es ![]() . Si sustituyes valores de x de
. Si sustituyes valores de x de ![]() a
a ![]() , los valores de
, los valores de ![]() irían de
irían de ![]() a
a ![]() , y
, y ![]() pasarían por otro ciclo completo de la función seno.
pasarían por otro ciclo completo de la función seno.
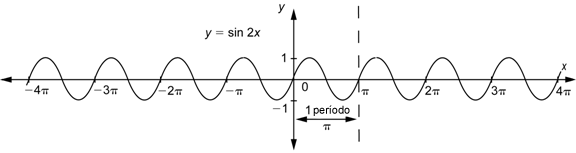
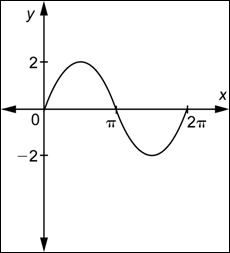
Observa que ![]() tiene dos ciclos en el intervalo [0, 2
tiene dos ciclos en el intervalo [0, 2![]() ], que es el intervalo
], que es el intervalo ![]() necesita para completar un ciclo completo.
necesita para completar un ciclo completo.
| ¿Cuál es el valor positivo más pequeño de x donde
A) B) C) D)
|
¿Cuál es el periodo de la función ![]() ? Aquí hay una tabla con algunas entradas y salidas para ésta función.
? Aquí hay una tabla con algunas entradas y salidas para ésta función.
| x (en radianes) | 3x (en radianes) | sen3x |
| 0 | 0 | 0 |
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
| 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0 |
Conforme los valores de x van de 0 a ![]() , los valores de
, los valores de ![]() van de 0 a
van de 0 a ![]() . Podemos ver de la gráfica que
. Podemos ver de la gráfica que ![]() hace un ciclo completo en el intervalo
hace un ciclo completo en el intervalo ![]() , por lo que su periodo es
, por lo que su periodo es ![]() .
.
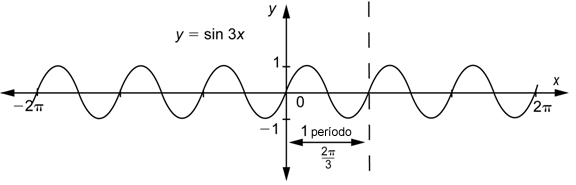
Observa que ![]() tiene tres ciclos en el intervalo [0, 2
tiene tres ciclos en el intervalo [0, 2![]() ], que es el intervalo
], que es el intervalo ![]() necesita para completar un ciclo completo.
necesita para completar un ciclo completo.
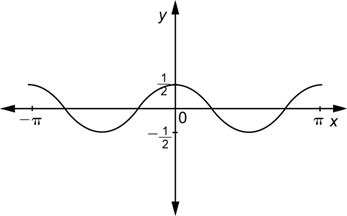
¿Cuál es el periodo de la función ![]() ? Aquí hay una tabla con algunas entradas y salidas para ésta función.
? Aquí hay una tabla con algunas entradas y salidas para ésta función.
| x (en radianes) |
| sen |
| 0 | 0 | 0 |
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
| 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0 |
Conforme los valores de x van de 0 a ![]() , los valores de
, los valores de ![]() van de 0 a
van de 0 a ![]() .
.
Podemos ver de la gráfica que ![]() hace un ciclo completo en el intervalo
hace un ciclo completo en el intervalo ![]() , entonces su periodo es
, entonces su periodo es ![]() .
.
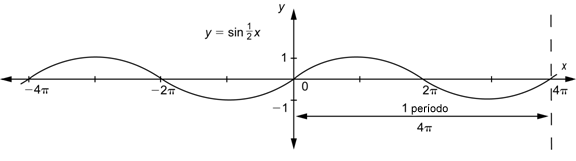
Observa que ![]() tiene medio ciclo en el intervalo [0, 2
tiene medio ciclo en el intervalo [0, 2![]() ], que es el intervalo
], que es el intervalo ![]() necesita para completar un ciclo completo.
necesita para completar un ciclo completo.
Pongamos éstos resultados en una tabla. Para las primeras tres funciones hemos reescrito sus periodos con el numerador ![]() para que el patrón sea claro. ¿Puedes ver la relación entre la función y el denominador en los periodos?
para que el patrón sea claro. ¿Puedes ver la relación entre la función y el denominador en los periodos?
| Función | Periodo |
|
|
|
|
|
|
|
|
|
|
|
|
En cada caso, el periodo podría encontrarse dividiendo ![]() entre el coeficiente de x. En general, el periodo de
entre el coeficiente de x. En general, el periodo de ![]() es
es ![]() , y el periodo de
, y el periodo de ![]() es
es ![]() . Como el periodo es la longitud del intervalo, siempre debe ser un número positivo. Como es posible que b sea un número negativo, debemos usar
. Como el periodo es la longitud del intervalo, siempre debe ser un número positivo. Como es posible que b sea un número negativo, debemos usar ![]() en la fórmula para asegurarte que el periodo,
en la fórmula para asegurarte que el periodo, ![]() , siempre sea un número positivo.
, siempre sea un número positivo.
| El periodo de
|
Puedes pensar en los distintos valores de b como teniendo un efecto “acordeón” (o resorte) en las gráficas de seno y coseno. Un valor grande de b las aplasta y un valor pequeño de b las estira.
Hay otra manera de describir éste efecto, En el intervalo ![]() ,
, ![]() pasa por un ciclo mientras
pasa por un ciclo mientras ![]() pasa por dos ciclos. Si regresas a los ejemplos anteriores, verás que
pasa por dos ciclos. Si regresas a los ejemplos anteriores, verás que ![]() tiene
tiene ![]() ciclos en el intervalo
ciclos en el intervalo ![]() . De la misma manera,
. De la misma manera, ![]() tiene
tiene ![]() ciclos en el intervalo
ciclos en el intervalo ![]() .
.
| Ejemplo | ||
| Problema | ¿Cuáles son los periodos de | |
|
|
| Para |
|
|
| Para |
| Respuesta | El periodo de | |
Amplitud
Como has visto, las gráficas de las funciones seno y coseno alternan lomas y valles. La altura de una loma (que es igual a la profundidad de un valle) se llama amplitud. Puedes ver que para todas las gráficas que hemos visto hasta ahora, la amplitud ha sido 1.
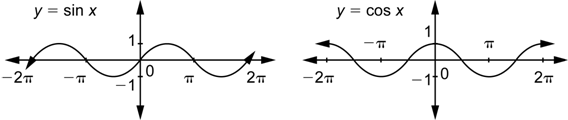
La manera formal de decir esto de una función periódica es:
![]()
Sabes que el valor máximo de ![]() o
o ![]() es 1 y el valor mínimo de ambas es
es 1 y el valor mínimo de ambas es ![]() . Entonces si aplicas la definición anterior, obtienes:
. Entonces si aplicas la definición anterior, obtienes:
![]()
El resultado concuerda con lo que ya habías observado en la gráfica.
Has visto que cambiar el valor de b en ![]() o
o ![]() estira o comprime la gráfica como un acordeón o un resorte, pero no cambia los valores máximo ni mínimo. Para todas estas funciones, el máximo es 1 y el mínimo
estira o comprime la gráfica como un acordeón o un resorte, pero no cambia los valores máximo ni mínimo. Para todas estas funciones, el máximo es 1 y el mínimo ![]() . Entonces si aplicas la definición de amplitud, estarías haciendo exactamente el mismo cálculo que hicimos anteriormente. La amplitud de cualquiera de estas funciones es 1.
. Entonces si aplicas la definición de amplitud, estarías haciendo exactamente el mismo cálculo que hicimos anteriormente. La amplitud de cualquiera de estas funciones es 1.
Veamos un tipo distinto de cambio en una función graficando la función ![]() . Aquí hay una tabla con algunos valores de ésta función.
. Aquí hay una tabla con algunos valores de ésta función.
| x (en radianes) | senx | 2senx |
| 0 | 0 | 0 |
|
|
| 1 |
|
|
|
|
|
|
|
|
|
| 1 | 2 |
|
|
|
|
|
|
|
|
|
|
| 1 |
|
| 0 | 0 |
Tomaremos la primera y la tercer columna para llenar la gráfica y luego extender el patrón a la izquierda y a la derecha.
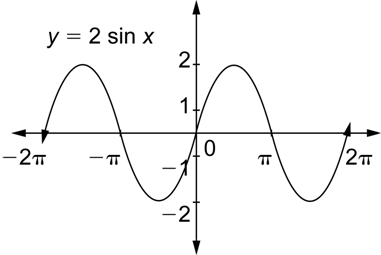
Ahora puedes usar ésta gráfica en el siguiente ejemplo.
| Ejemplo | ||
| Problema | ¿Cuál es la amplitud de | |
|
|
| Puedes encontrar los valores máximo y mínimo de la función a partir de la gráfica. Por ejemplo, en |
|
|
| Usa la definición de amplitud. |
|
| Observa que la altura de cada loma es 2, y la profundidad de cada valle es 2. Esto es igual a la amplitud, como se mencionó al principio. | |
|
| Observa también que la amplitud es igual al coeficiente de la función: Esto no es una coincidencia. | |
| Respuesta | La amplitud es 2. |
|
Comparemos la gráfica de ésta función con la gráfica de la función seno.
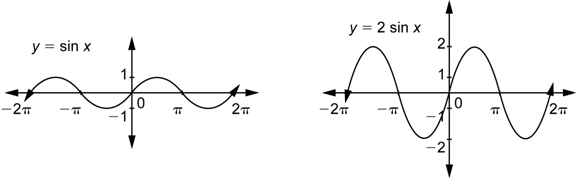
El efecto de multiplicar ![]() por 2 es estirar la gráfica verticalmente por un factor de 2. Como ha sido estirada en la vertical por éste factor; la amplitud es el doble, o 2. Si hubiéramos usado
por 2 es estirar la gráfica verticalmente por un factor de 2. Como ha sido estirada en la vertical por éste factor; la amplitud es el doble, o 2. Si hubiéramos usado ![]() , la gráfica hubiera sido estirada verticalmente por un factor de 3, y la amplitud de ésta función es 3. Una vez más, esto es igual a l coeficiente de la función. En general, tenemos la siguiente regla.
, la gráfica hubiera sido estirada verticalmente por un factor de 3, y la amplitud de ésta función es 3. Una vez más, esto es igual a l coeficiente de la función. En general, tenemos la siguiente regla.
| La amplitud de
|
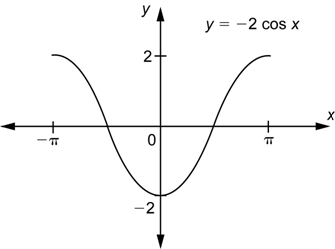
Como último ejemplo, ![]() , muestra que multiplicar por una constante afecta la amplitud. Si multiplicas por una constante por fuera y por dentro, como en
, muestra que multiplicar por una constante afecta la amplitud. Si multiplicas por una constante por fuera y por dentro, como en ![]() , vas a afectar la amplitud y el periodo. Aquí hay una gráfica de
, vas a afectar la amplitud y el periodo. Aquí hay una gráfica de ![]() :
:
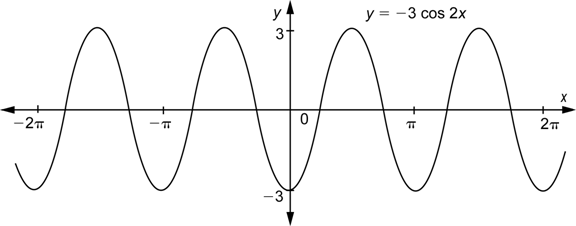
| Ejemplo | ||
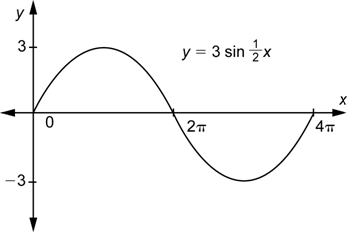
| Problema | Determinar la amplitud y el periodo de | |
|
|
| Usa la fórmula para la amplitud, con |
|
|
| Usa la fórmula para el periodo, con |
| Respuesta | La amplitud es 3 y el periodo es |
|
En este ejemplo, pudiste haber encontrado el periodo observando la gráfica anterior. Se muestra un ciclo completo, por ejemplo, en el intervalo ![]() , entonces el periodo es
, entonces el periodo es ![]() .
.
En las funciones ![]() y
y ![]() , multiplicar por una constante sólo afecta la amplitud, no el periodo. Como dijimos antes, cambiar el valor de b sólo afecta el periodo, no la amplitud. El resultado general es como sigue.
, multiplicar por una constante sólo afecta la amplitud, no el periodo. Como dijimos antes, cambiar el valor de b sólo afecta el periodo, no la amplitud. El resultado general es como sigue.
| La amplitud de
El periodo de
|
Para ayudarte a entender los cambios en la amplitud y el periodo para ambas funciones seno y coseno, intenta con el siguiente ejemplo interactivo:
| ¿Cuál es la amplitud y el periodo de
A) La amplitud es B) La amplitud es C) La amplitud es 1, y el periodo es D) La amplitud es 1, y el periodo es
|
Sabes que la función ![]() tiene amplitud
tiene amplitud ![]() y periodo
y periodo ![]() . Puedes usar estos hechos para dibujar la gráfica de cualquier función en la forma
. Puedes usar estos hechos para dibujar la gráfica de cualquier función en la forma ![]() empezando con la gráfica de
empezando con la gráfica de ![]() y modificándola.
y modificándola.
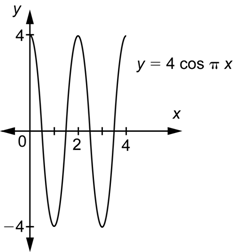
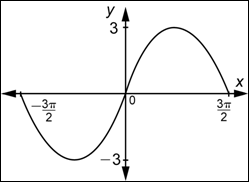
Por ejemplo, supongamos que quieres graficar ![]() . Como
. Como ![]() , ésta función tiene el mismo periodo que
, ésta función tiene el mismo periodo que ![]() . Ya que
. Ya que ![]() , la amplitud es 4. Entonces, tomarías la gráfica de
, la amplitud es 4. Entonces, tomarías la gráfica de ![]() y simplemente la estiras verticalmente por un factor de 4. Aquí hay un ciclo para estas dos funciones.
y simplemente la estiras verticalmente por un factor de 4. Aquí hay un ciclo para estas dos funciones.
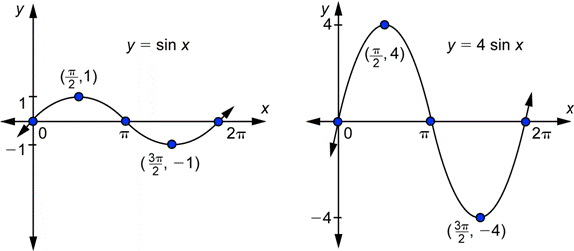
Nota que los puntos que estaban en el eje-x “se quedan” en el eje-x. En estos puntos (donde ![]() ), el valor de
), el valor de ![]() es 0. Si multiplicas 0 por 4 (u otra cosa), seguirás teniendo el valor de 0. Entonces los puntos siguen en el eje-x. Por otro lado, los puntos más alto y más bajo se han alejado del eje-x. Tienen valores en y de 1 y
es 0. Si multiplicas 0 por 4 (u otra cosa), seguirás teniendo el valor de 0. Entonces los puntos siguen en el eje-x. Por otro lado, los puntos más alto y más bajo se han alejado del eje-x. Tienen valores en y de 1 y ![]() para
para ![]() , y tienen valores en y de 4 y
, y tienen valores en y de 4 y ![]() para
para ![]() .
.
| Ejemplo | |
| Problema | Graficar |
|
| El valor de b es 1, entonces la gráfica tiene un periodo de |
|
| El valor de a es |
|
| Si bien la amplitud y el periodo son iguales en la función
|
| Respuesta |
|
Si quieres revisar éstas gráficas con una calculadora graficadora, asegúrate de que la pantalla tenga los parámetros correctos. Para el último ejemplo, usarías ![]() y
y ![]() . En general, querrías ajustar los valores de x para mostrar un ciclo completo y los valores de y para la amplitud.
. En general, querrías ajustar los valores de x para mostrar un ciclo completo y los valores de y para la amplitud.
Si los valores de a y b son distintos de 1, entonces necesitas combinar los efectos de los dos cambios.
| Ejemplo | |
| Problema | Graficar |
|
| El valor de a es 3, entonces la gráfica tiene amplitud 3. Esto tiene un efecto de tomar la gráfica de |
|
| El valor de bes |
|
| Para hacer la gráfica de |
|
|
|
| Respuesta |
|
Algunas veces necesitas estirar la gráfica de la función seno, y a veces necesitas comprimirla.
| Ejemplo | |
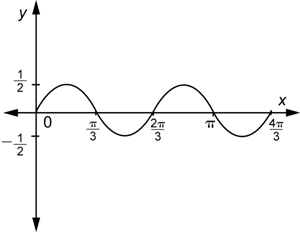
| Problema | Graficar dos ciclos de una función seno cuya amplitud es |
|
| Hay diferentes funciones de la forma |
|
| Como la amplitud es |
|
| El periodo es |
|
| Para hacer la gráfica, debes combinar ambos efectos. |
| Respuesta |
|
Incluso sin saber el valor específico de una constante, a veces puedes reducir las posibilidades de la forma de una gráfica.
| La gráfica de una función
¿Cuál de las siguientes opciones podría ser la gráfica?
A) B)
C) D)
|
Sabes que la función ![]() tiene amplitud
tiene amplitud ![]() y periodo
y periodo ![]() . De la misma forma que hicimos con las funciones seno, puedes usar éstos hechos para dibujar la gráfica de cualquier función en la forma
. De la misma forma que hicimos con las funciones seno, puedes usar éstos hechos para dibujar la gráfica de cualquier función en la forma ![]() empezando con la gráfica de
empezando con la gráfica de ![]() y modificándola.
y modificándola.
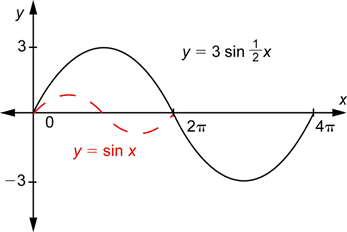
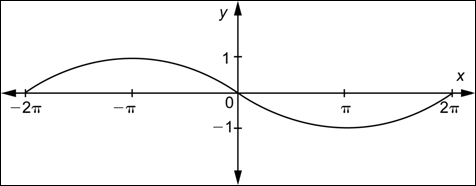
Por ejemplo, supongamos que quieres graficar ![]() . Como
. Como ![]() , tiene la misma amplitud que
, tiene la misma amplitud que ![]() . Y, como
. Y, como ![]() , el periodo está dado por:
, el periodo está dado por:
![]()
Como es el doble del periodo de ![]() , tomarías la gráfica de
, tomarías la gráfica de ![]() y la estirarías horizontalmente por un factor de 2. Aquí vemos una comparación de ambas gráficas.
y la estirarías horizontalmente por un factor de 2. Aquí vemos una comparación de ambas gráficas.
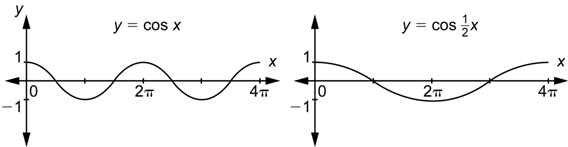
Observa que en el intervalo ![]() , la gráfica de
, la gráfica de ![]() tiene un ciclo completo. Como
tiene un ciclo completo. Como ![]() , la gráfica de
, la gráfica de ![]() tiene
tiene ![]() de un ciclo en ese intervalo.
de un ciclo en ese intervalo.
Si usas una calculadora graficadora, necesitas ajustar los parámetros de cada gráfica para obtener una ventana que muestra todas las características de la gráfica. Por ejemplo, usarías ![]() y
y ![]() . En general, probablemente querrías ajustar los valores de x para mostrar un ciclo completo y los valores de y para mostrar los puntos alto y bajo. En el siguiente ejemplo, usarías
. En general, probablemente querrías ajustar los valores de x para mostrar un ciclo completo y los valores de y para mostrar los puntos alto y bajo. En el siguiente ejemplo, usarías ![]() y
y ![]() para la ventana de la gráfica porque se te pide graficar en el dominio
para la ventana de la gráfica porque se te pide graficar en el dominio ![]() y la gráfica tendrá una amplitud de 2, que iría desde -2 hasta +2.
y la gráfica tendrá una amplitud de 2, que iría desde -2 hasta +2.
| Ejemplo | |
| Problema | Graficar |
|
| La amplitud es igual a |
|
| El valor de b es 1, por lo que la gráfica tiene periodo |
|
| Cuando el único cambio es estirar verticalmente, comprimir, o cambiar, las intersecciones en x son las mismas, Entonces la gráfica va a pasar por el eje x en |
| Respuesta |
|
Una vez más, si los valores de a y b son distintos de 1, necesitas combinar los efectos de los dos cambios, En el siguiente ejemplo, habrá una variación que no habías visto antes. Hasta ahora, todos los valores de b han sido números racionales, pero aquí estamos usando el número irracional ![]() . Esta situación realmente no cambia el procedimiento, pero verás que cambia la escale del eje-x de una manera distinta.
. Esta situación realmente no cambia el procedimiento, pero verás que cambia la escale del eje-x de una manera distinta.
| Ejemplo | |
| Problema | Graficar |
|
| El valor de a es 4, entonces la gráfica tiene una amplitud de 4. Esto tiene el efecto de tomar la gráfica de |
|
| El valor de bes |
|
| Observa el efecto en los valores de x de las intersecciones, los puntos altos, y los puntos bajos. Como el periodo es 2, el primer ciclo de la gráfica tendrá puntos altos en |
|
| Para hacer la gráfica de |
| Respuesta |
|
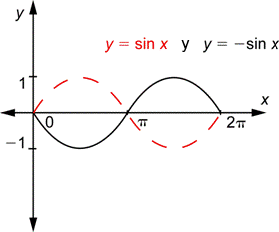
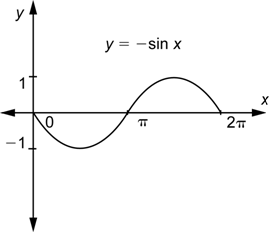
En los dos ejemplos anteriores (![]() y
y ![]() ) viste que el signo negativo afuera (un valor negativo de a) tiene el efecto de voltear la gráfica sobre el eje-x. En el siguiente ejemplo, verás el efecto del signo negativo cuando está “dentro” (un valor negativo de b).
) viste que el signo negativo afuera (un valor negativo de a) tiene el efecto de voltear la gráfica sobre el eje-x. En el siguiente ejemplo, verás el efecto del signo negativo cuando está “dentro” (un valor negativo de b).
Una última pista: además de intentar encontrar el efecto general del valor de a o b en la gráfica, podrías también querer revisar puntos específicos. Por ejemplo, simplemente sustituye ![]() en la función y ve dónde queda ese punto.
en la función y ve dónde queda ese punto.
| ¿Cuál de las siguientes opciones es la gráfica de
A) B)
C) D)
|
Dada una función en la forma ![]() o
o ![]() , sabes cómo encontrar la amplitud y el periodo y cómo usar ésta información para graficar las funciones.
, sabes cómo encontrar la amplitud y el periodo y cómo usar ésta información para graficar las funciones.
Dada una gráfica de una función seno o coseno, también puedes determinar la amplitud y el periodo de la función. A partir de ésta información, puedes encontrar los valores de a y b, y luego una función que corresponda a la gráfica.
Recuerda que junto con encontrar la amplitud y el periodo, es buena idea observar lo que pasa en ![]() . Si a y b son constantes distintas de cero, las funciones
. Si a y b son constantes distintas de cero, las funciones ![]() y
y ![]() tendrán los siguientes valores en
tendrán los siguientes valores en ![]() :
:
![]()
Esto te dice que la gráfica de ![]() pasa por
pasa por ![]() sin importar los valores de a y b, y la gráfica de
sin importar los valores de a y b, y la gráfica de ![]() nunca pasa por
nunca pasa por ![]() sin importar los valores de a y b. Entonces, por ejemplo, si te dan una gráfica que pasa por el origen y te piden determinar una función que la represente, sabes inmediatamente que no está en la forma de
sin importar los valores de a y b. Entonces, por ejemplo, si te dan una gráfica que pasa por el origen y te piden determinar una función que la represente, sabes inmediatamente que no está en la forma de ![]() .
.
Necesitas tener cuidado con el signo de a. Podrías determinar que una función tiene una amplitud de 4, por ejemplo. Aunque es posible que ![]() , también es posible que
, también es posible que ![]() . Aquí hay un ejemplo de cada una de éstas posibilidades.
. Aquí hay un ejemplo de cada una de éstas posibilidades.
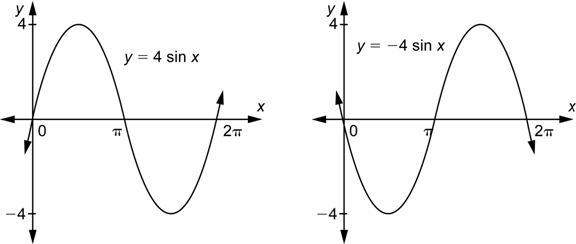
Necesitarás comparar la gráfica con la de ![]() o
o ![]() para ver si, además de estirar o comprimir, ha ocurrido una reflexión en el eje-x. La gráfica anterior en la derecha puede pasar como un resultado de estirar y reflejar la gráfica de
para ver si, además de estirar o comprimir, ha ocurrido una reflexión en el eje-x. La gráfica anterior en la derecha puede pasar como un resultado de estirar y reflejar la gráfica de ![]() por el eje-x. Si ha habido una reflexión, entonces el valor de a será negativo. Una vez que has determinado si a es positivo o negativo, puedes escoger un valor positivo para b.
por el eje-x. Si ha habido una reflexión, entonces el valor de a será negativo. Una vez que has determinado si a es positivo o negativo, puedes escoger un valor positivo para b.
Aquí hay algunos ejemplos de éste proceso.
| Ejemplo | |
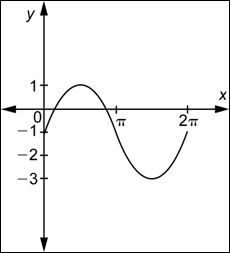
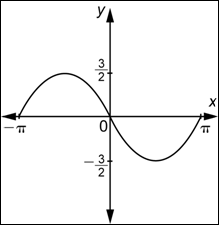
| Problema | Determinar una función de la forma
|
|
| Primero, observa que la gráfica pasa por el origen, por lo que estás viendo una función de la forma |
|
| Ahora, observa que el valor máximo de la función es 2 y el mínimo es |
|
| Finalmente, observa que la gráfica muestra dos ciclos y que un ciclo completo está contenido en el intervalo |
|
| Combina éstas tres piezas de información. |
| Respuesta |
|
| Ejemplo | |
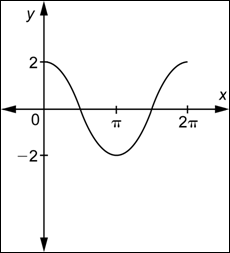
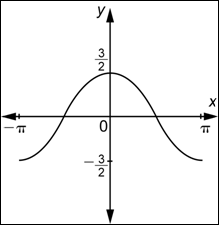
| Problema | Determinar una función de la forma
|
|
| Primero, observa que la gráfica no pasa por el origen, sino por las crestas, alcanzando el máximo cuando x = 0, por lo que estás buscando una función de la forma |
|
| Ahora, observa que el valor mínimo de la función es |
|
| Finalmente, observa que la gráfica muestra dos ciclos y que un ciclo completo está contenido en el intervalo |
|
| Combina éstas tres piezas de información. |
| Respuesta |
|
Asegúrate de que reconoces dónde comienza y termina un ciclo, El periodo es la longitud del intervalo por el que corre el ciclo.
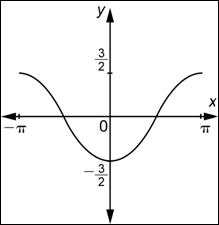
| ¿Cuál de las siguientes funciones está representada por la gráfica siguiente?
A) B) C) D)
|
Recuerda que cuando escribes una función puedes usar la notación ![]() en lugar de la variable y.
en lugar de la variable y.
| ¿Cuál de las siguientes gráficas representa
A) B) C) D)
|
Sumario
Las funciones ![]() y
y ![]() son funciones periódicas: sus gráficas tienen un patrón repetido de lomas y valles que continúa infinitamente en ambas direcciones. La altura de una loma o la profundidad de un valles se llama amplitud, y es igual a
son funciones periódicas: sus gráficas tienen un patrón repetido de lomas y valles que continúa infinitamente en ambas direcciones. La altura de una loma o la profundidad de un valles se llama amplitud, y es igual a ![]() .Cualquier patrón completo en la gráfica se llama ciclo, y la longitud de un intervalo en donde ocurre un ciclo se llama periodo. El periodo es igual al valor
.Cualquier patrón completo en la gráfica se llama ciclo, y la longitud de un intervalo en donde ocurre un ciclo se llama periodo. El periodo es igual al valor ![]() .
.
Puedes usar ésta información para graficar cualquiera de estas funciones empezando con la gráfica básica de ![]() o
o ![]() y luego hacer una combinación de estirar o comprimir la gráfica verticalmente basado en el valor de a, estirar y comprimir la gráfica horizontalmente basado en el valor de b, o reflejándola basado en los signos de a y b.
y luego hacer una combinación de estirar o comprimir la gráfica verticalmente basado en el valor de a, estirar y comprimir la gráfica horizontalmente basado en el valor de b, o reflejándola basado en los signos de a y b.
También puedes empezar con una gráfica, determinar los valores de a y b, y luego determinar una función que la represente.