Degree and Radian Measure

Learning Objectives

Understand radian measure.
Convert from degree to radian measure.
Convert from radian to degree measure.

Introduction

You know that there can be different units of measurement to measure the same thing. For example, length can be measured in feet and meters and temperature can be measured in degrees Celsius and degrees Fahrenheit. We often use formulas to convert between different units of measurement.

There are also two ways to measure angles. You know how to measure them in degrees. Now you will learn how to measure them in radians and how to convert between these two measurements. While degree measure is used in everyday activities such as building construction and surveying land, radian measureA measure of a central angle given by the ratio of the arc length to the radius. is used for many calculations, such as the speed and distance traveled by satellites above the Earth’s surface, including the International Space Station! It is important to be able to measure angles in radians as well as in degrees and to be able to convert between the two systems.

Radian Measure

In order for us to be able to define radians, it is necessary to introduce the concept of a central angle. A central angleAn angle whose vertex is at the center of a circle. is an angle whose vertex is at the center of a circle. In the circle below, the center is point `O`, the length of the radius is `r`, and `/_AOB` is a central angle.

An image shows a circle with central angle A O B. The center is point O and points A and B are on edges of the circle. Labels show radii OA and OB to be of length R and the arc they cut off on the circle to be of length S. The measure of angle A O B is labeled theta.

Notice that `/_AOB` cuts off or determines an arc `overset(frown)(AB)` that has length `s`. The radian measure of a central angle, often denoted by the Greek letter theta (`theta`), is defined to be the ratio of the arc length to the length of the radius. So the radian measure of `/_AOB` is given by:

`theta="arc length"/"radius length"=s/r`

Arc length, `s`, and radius, `r`, must be in the same units.

Example
Problem	*What is the radian measure of central angle `AOB`?*
	`theta=s/r=(6" inches")/(3" inches")=2`	In this circle, `r=3` inches. The arc determined by `/_AOB` has length `s=6` inches. Substitute these into the formula.
Answer	The measure of central angle `AOB` is `2` radians.

Example
Problem	Find the measure of central angle `AOB` in radians.
	`theta=s/r=(pi/3" cm")/(1" cm")=pi/3`	In this circle, `r=1" cm"`. The arc determined by `/_AOB` has length `s=pi/3" cm"`. Substitute these into the formula.
Answer	The measure of central angle `AOB` is `pi/3` radians.

What is the connection between degrees and radians? Let’s see what happens when the arc is the entire circle:

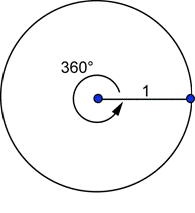
An image shows a circle with a central angle labeled 360 degrees. The radius is 1.

The circumference of this circle is given by `C=2pir=2pi*1=2pi`. This is the arc length of the entire circle, or the arc length corresponding to a central angle of `360^@`. What is the radian measure of this angle?

`theta="arc length"/"radius length"=(2pi)/1=2pi`

A central angle of `360^@` has a radian measure of `2pi`. That is:

`360^@=2pi " radians"`

If you divide both sides by `2`, you will obtain:

`180^@=pi " radians"`

We’ll use this to convert from degrees to radians and vice versa.

While degrees are always written with a degree symbol (°), radians are usually written without any symbol or unit attached. So, for example, `tan3^@` means the tangent of an angle that measures `3^@`, while `tan3` means the tangent of an angle that measures `3` radians.

Make sure that you use the same units of length for the length of the radius `r` and the arc length `s`. In the first example, they were both in inches; in the second example, they were both in centimeters. When you divide, those units cancel, and you are left with a unitless number.

Example

Problem

Find the measure of central angle `AOB` in radians.

`s`	`=`	`48 " inches"`
	`=`	`48 " inches"*(1 " foot")/(12 " inches")`
	`=`	`4 " feet"`

You want the arc length and the radius to have the same units, but they are given to you in inches and feet. You could convert either one. The arc determined by `/_AOB` has length `s=48` inches.

`theta=s/t=(4 " feet")/(2 " feet")=2`

In this circle, `r=2` feet. Substitute this and the value above for `s` into the formula.

Answer

The measure of central angle `AOB` is `2` radians.

If you take the definition of radian measure, `theta=s/r`, and multiply both sides by `r`, you get the formula for arc length:

`s=r theta`

Example
Problem	The central angle shown has a measure of `1/2` radian. What is the length of `overset(frown)(CD)`?
	`s=r theta=(4 " inches")*1/2=2 " inches"`	In this circle, `r=4` inches. You know that `theta=1/2`. Substitute these numbers into the arc length formula.
Answer	The length of `overset(frown)(CD)` is `2` inches.

We have used `theta=s/t` and `s=r theta` to find the radian measure of the central angle as well as the arc length. But you can also use the arc length formula to find the length of the radius, as seen in the following example.

Example
Problem	If the length of `overset(frown)(EF)` is `42` millimeters, and the measure of `/_EOF` is `3` radians, what is the length of the radius of the circle?
	`s=r theta` `42 " mm"=r*3`	You are given that `s=42 " mm"`, and `theta=3`. Substitute these values into the arc length formula.
	`(42 " mm")/3=r`	Solve the equation for `r`.
	`r=14 " mm"`	Rewrite as a mixed number.
Answer	The radius of the circle is `14` millimeters.

A circle has a radius of `8` inches and central angle `AOB` makes an arc `AB` of length `2` feet.

What is the radian measure of angle `AOB`?

A) `1/4`

B) `1/3`

C) `3`

D) `4`

Show/Hide Answer

Converting from Degrees to Radians

Earlier we saw that `180^@=pi " radians"`. Divide both sides of this equation by `180`. You get:

`1^@=pi/180 " radians"`

You can use this to convert the measure of an angle from degrees to radians. For example, if you wanted to convert `30^@` to radians, you could multiply both sides by `30`:

`30^@=30*pi/180 " radians"=(30pi)/180 " radians"=pi/6 " radians"`

To say this another way, you multiply `30^@` by `pi/180^@` to get `pi/6 " radians"`.

To convert `60`° to radians, you multiply `60^@` by `pi/180^@` to get `pi/3 " radians"`.

In a similar fashion, multiply any degree measure by `pi/180^@` to convert it to radians.

Example

Problem

Convert `0^@`, `45^@`, and `90^@` to radians.

`0^@=0^@*pi/180^@ " radians"=0 " radians"`

In each case, just multiply by `pi/180^@` and simplify.

`45^@`	`=`	`45^@*pi/180^@ " radians"`
	`=`	`(45pi)/180 " radians"`
	`=`	`pi/4 " radians"`


`90^@`	`=`	`90^@*pi/180^@ " radians"`
	`=`	`(90pi)/180 " radians"`
	`=`	`pi/2 " radians"`

Answer

`0^@=0 " radians"`, `45^@=pi/4 " radians"`, `90^@=pi/2 " radians"`

Here is a chart with the angles that we have converted so far.

Degree Measure	Radian Measure
`0^@`	`0`
`30^@`	`pi/6`
`45^@`	`pi/4`
`60^@`	`pi/3`
`90^@`	`pi/2`
`180^@`	`pi`
`360^@`	`2pi`

Here is the same information, with some additional angles, in a picture format:

The same procedure works just as well for negative angles. Remember that a negative angle is just an angle that is oriented clockwise when drawn in standard position. A negative number of degrees becomes a negative number of radians.

How many radians are there in `-120^@`?

A) `pi/60`

B) `-2/3`

C) `-(3pi)/2`

D) `-(2pi)/3`

Show/Hide Answer

Converting from Radians to Degrees

Suppose you had angles measured in radians and you wanted to know their degree measure. The procedure is similar to the one going from degrees to radians.

Again, you know that `pi " radians"=180^@`. Divide both sides of this equation by `pi`. You get:

`1 " radian"=180^@/pi`

If you wanted to convert `pi/6` radians to degrees, you could multiply both sides of the above equation by `pi/6`:

`pi/6*1 " radian"=pi/6*180^@/pi=180^@/6=30^@`

To state this in another way, we multiplied `pi/6` by `180^@/pi` to get `30^@`. In a similar fashion, multiply any radian measure by `180^@/pi` to convert it to degrees.

Example

Problem

Convert `(2pi)/3` and `(3pi)/4` to degrees.

`(2pi)/3`	`=`	`(2pi)/3*180^@/pi`
	`=`	`360^@/3`
	`=`	`120^@`

In each case, just multiply by `180^@/pi` and simplify.

`(3pi)/4`	`=`	`(3pi)/4*180^@/pi`
	`=`	`540^@/4`
	`=`	`135^@`

Answer

`(2pi)/3=120^@`, `(3pi)/4=135^@`

Make sure that your answer has a degree symbol. An angle measure written without a degree symbol is always assumed to be in radians.

Here is a chart showing equivalent radian and degree measures for some common angles.

Radian Measure	Degree Measure
`0`	`0^@`
`pi/6`	`30^@`
`pi/4`	`45^@`
`pi/3`	`60^@`
`pi/2`	`90^@`
`pi`	`180^@`
`2pi`	`360^@`

Example

Problem

Convert `1` radian to degrees and give your answer to the nearest tenth of a degree.

`1 " radian"`	`=`	`180^@/pi`
	`=`	`57.29577951^@...`
	`=`	`~~57.3^@`

Actually, you already know the value of `1` radian in degrees. However, you need to use a calculator to do the division and obtain a decimal.

Answer

`1 " radian"~~57.3^@`

So `1` radian is a little less than `60^@`, or a little less than one-sixth of a circle.

You can use the same procedure for negative angles.

What is the equivalent degree measure of `-(5pi)/6` radians written in simplest terms?

A) `150^@`

B) `-150^@`

C) `(-900^@)/6`

D) `(-pi^2)/216`

Show/Hide Answer

Summary

Angles can be measured in two ways: with degrees and radians. Radian measure of a central angle is defined as the ratio of the arc length to the length of the radius. This definition leads to the arc length formula: `s=rtheta`.

Radians and degrees are connected by the relationship `360^@=2pi " radians"`. If you wish to convert from degrees to radians, multiply the degree measure by `pi/180^@`. If you wish to convert from radians to degrees, multiply the radian measure by `180^@/pi`.