Introduction to Logarithmic Functions

A useful family of functions that is related to exponential functionsA function of the form `f(x)=b^x` where `b>0` and `b!=1`. is the logarithmic functionsA function using a logarithm, of the form `f(x)=log_bx, b>0` and `b!=1`. A calculation in which the exponent `y` in `x=b^y` is found when given `x` and `b`; the corresponding notation is `log_bx=y`. . You have been calculating the result of `b^x`, and this gave us the exponential functions. A logarithmA calculation in which the exponent `y` in `x=b^y` is found when given `x` and `b`; the corresponding notation is `log_bx=y`. is a calculation of the exponentWhen a number is expressed in the form `a^b`, `b` is the exponent. The exponent indicates how many times the base is used as a factor. Power and exponent mean the same thing. in the equation `y = b^x`. Put another way, finding a logarithm is the same as finding the exponent to which the given base must be raised to get the desired value. The exponent becomes the output rather than the input.

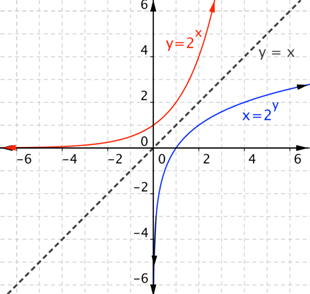
Note the two tables are the same except the columns are reversed: the point `(1, 2)` taken from the first table will be the point `(2, 1)` in the second table.

The graphs of these two relationships should have the same general shape. As shown in the graph, the two curves are symmetrical about the line `y = x`. Another way to put it, if you rotate the red curve about the line `y = x`, it will coincide with the blue curve. (This makes sense, because `y` in the first table becomes `x` in the second table, and vice versa.)

The equation `x=2^y` is often written as a logarithmic function (called log function for short). The logarithmic function for `x=2^y` is written as `y=log_2x` or `f(x)=log_2x`. The number `2` is still called the baseThe expression that is being raised to a power when using exponential notation. In `5^3`, `5` is the base which is the number that is repeatedly multiplied. `5^3=5*5*5`. And in `a^b`, the base is `a`.. In general, `y=log_bx` is read, “`y` equals log to the base `b` of `x`,” or more simply, “`y` equals log base `b` of `x`.” As with exponential functions, `b>0` and `b!=1`.

You can see from the graph that the range (`y` values) of the exponential function (in red) is positive real numbers. Since the input and output have been switched, the domain (`x` values) of the logarithmic function (in blue) is positive real numbers.

Similarly, the domain of the exponential function (in red) is all real numbers. The range of the logarithmic function (in blue) is all real numbers.

It’s important to remember that the result of a logarithm is the exponent! That is, `log_b x`asks, “What exponent on the base `b` will give the result `x`?”

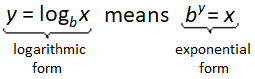
Sometimes, you will need to convert `log_bx=y` to `b^y=x`. Other times, you will convert `b^y=x` to `log_bx=y`. The examples in the table show the logarithmic form and the corresponding exponential form of several equations.

Knowing this connection is essential to understanding, and working with, logarithms.

Example

Problem

Rewrite `log_3 9 = 2` as an exponential equation.

`log_bx=y hArr b^y=x`

`log_3`	`9`	`=`	`2`
`b=3`	`x=9`		`y=2`

`b^y=x rArr 3^2=9`

You need to change `log_3 9=2` to the form `b^y=x`.

Here the base is `3` and the exponent is `2`.

Substitute for `b`, `y`, and `x` in the exponential equation, `b^y=x`.

Answer

`3^2 = 9`

Check the result: Is `3^2` actually equal to `9`? Yes!

Although the input of a logarithm must always be positive, the result (an exponent!) can be negative.

Example

Problem

Convert `log_4(1/16)=-2` into an exponential equation.

`log_bx=y hArr b^y=x`

`log_4`	`1/16`	=	`-2`
`b=4`	`x=1/16`		`y=-2`

`b^y=x rArr4^-2=1/16`

You need to rewrite `log_4(1/16)=-2` in the form `b^y=x`.

Here the base is `4` and the exponent is `-2`.

Substitute for `b`, `y`, and `x` in the exponential equation, `b^y=x`.

Answer

`4^-2=1/16`

Check the result: `4^-2=(1/4)^2=1/4^2=1/16`

As you have just seen, it is possible to convert log equations into exponential equations. It is also possible to convert exponential equation into log equations.

Example
Problem	Rewrite `5^3 = 125` as a logarithmic equation.
	`b^y=x hArr log_bx=y` `5^3=125` `log_bx=y rArrlog_5 125=3`	You need to rewrite `5^3=125` in the form`log_b x = y`. Here the base is `5` and the exponent is `3`. Substitute for `b`, `y`, and `x` in the logarithmic equation, `log_bx=y`.
Answer	`log_b125 = 3`

Example
Problem	Convert `10^-3=1/(1,000)` into a logarithmic equation.
	`b^y=x hArr log_bx=y` `10^-3=1/(1,000)` Where `b=10^-3` and `y=-3` and `x=1/(1,000)` `log_bx=y rArr log_10(1/(1,000))=-3`	You need to rewrite `10^-3=1/(1,000)` in the form `log_bx = y`. Here the base is `10` and the exponent is `-3`. Substitute for `b`, `y`, and `x` in the logarithmic equation, `log_bx=y`.
Answer	`log_10 \ 1/(1,000)=-3`

Example
Problem	Convert `sqrt49=7` into a logarithmic equation.
	`sqrt49=49^(1/2)` `b^y=x hArr log_bx=y` `49^(1/2)=7`	Rewrite the square root using a fractional exponent. You need to rewrite `49^(1/2)=7` in the form `log_bx = y`.
	Where `b=49` and `y=(1/2)` and `x=7` `log_bx=y rArr log_49 7=1/2`	Here, the base is `49` and the exponent is `1/2`. Substitute for `b`, `y`, and `x` in the logarithmic equation, `log_b x=y`.
Answer	`log_49 7=1/2`

Look at the graph below. It should look familiar: you saw it earlier in this topic! The blue graph is the logarithmic function, and the red graph is the corresponding exponential function.

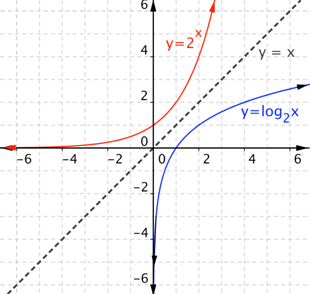
When graphing logarithmic functions, it’s important to remember the following:

Remember that logarithmic functions almost act like exponential functions. You just have to switch the `x` and `y` values. For example, the second bulleted item above is like the exponential function getting close to the `x`-axis (close to `y=0`).

Example

Problem

Graph `f(x) = log_3 x`.

Graph `y = log_3 x`.

This is the same as `3^y=x`.

To make the calculations easier, first make this a logarithmic equation in `y`. Then convert the logarithm into an exponential equation.

`x = 3^y`	`y`
	`-2`
	`-1`
	`0`
	`1`
	`2`

Start with a table of values.

With logarithmic functions, it’s usually easier to choose the `y` values instead of the `x` values. Be sure to include some negative values for `y`.

`x = 3^y`	`y`
`1/9`	`-2`
`1/3`	`-1`
`1`	`0`
`3`	`1`
`9`	`2`

Be careful with the negative exponents!

Use the table as ordered pairs. Remember that the graph of the function will show all `x - y` correspondences, so any pair that could be in the table must be on the graph.

A graph shows a coordinate plane with 5 points at the following coordinates: (one-ninth, negative 2); (one-third, negative 1); (1, zero); (3, 1); (9, 2).

Plot the points.

Answer

Since the points are not on a line, you can’t use a straightedge. Connect the points as best you can, using a smooth curve (not a series of straight lines).

Remember that logarithmic functions get close to the `y`-axis (but won’t touch or cross it).

Example

Problem

Graph `f(x) = log_4 x`.

Graph `y = log_4 x`.

This is the same as `4^y=x`.

To make the calculations easier, first make this a logarithmic equation in `y`. Then convert the logarithm into an exponential equation.

`x = 4^y`	`y`
`1/16`	`-2`
`1/4`	`-1`
`1`	`0`
`4`	`1`
`16`	`2`

Start with a table of values, choosing the `y` values and calculating `x`.

Be careful with the negative exponents!

A graph shows a coordinate plane with 5 points at the following coordinates: (one-sixteenth, negative 2); (one-fourth, negative 1); (1, zero); (4, 1); (8, three-halves).

Use the table as ordered pairs and plot the points.

In this case, `(16, 2)` won’t show on the graph. Because you know the square root of `4`, try `x=3/2`. In this case, it would be `4^(3/2)=(sqrt4)^3=2^3=8`. That point is shown in blue.

Answer

Since the points are not on a line, you can’t use a straightedge. Connect the points as best you can, using a smooth curve (not a series of straight lines).

Remember that logarithmic functions get close to the `y`-axis (but won’t touch or cross it).

Let’s compare the logarithmic graphs you’ve seen: `f(x) = log_2 x`, `f(x) = log_3 x`, and `f(x) = log_4 x`.

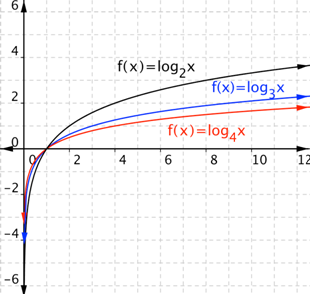
Notice that a larger base makes the graph less steep. (This is the opposite from exponential functions, where a larger base meant a steeper graph.) A larger base also makes the graph closer to the `x`-axis for `y>0` (or `x>1`) and closer to the `y`-axis for `y<0` (or `x<1`). All the graphs go through `(1, 0)`, while exponential functions always go through `(0, 1)`.

With exponential functions, the graphs were increasing (exponential growth) when the base `b` was greater than `1`. The graphs were decreasing (exponential decay) when the base `b` was less than `1`. The logarithmic graphs above are all increasing, and they all have a base greater than `1`. Let’s see what happens with a base less than `1`.

Example

Problem

Graph `f(x)=log_(1/4) x`.

`y=log_(1/4) x`

`(1/4)^y=x`

Write an exponential equation in `y` to help you.

`x`	`y`
`16`	`-2`
`4`	`-1`
`1`	`0`
`1/4`	`1`
`1/16`	`2`

Create a table of values. Again, remember to be careful with the negative exponents. Remember to take the reciprocal of the base to make the exponent positive. `(1/4)^-2=(4/1)^2=4^2=16`.

Notice that in this table, the `x` values decrease as the `y` values increase.

A graph shows a coordinate plane with 5 points at the following coordinates: (one-sixteenth, 2); (one-fourth, 1); (1, zero); (4, negative 1); (8, negative three-halves).

Use the table pairs to plot points. You may want to include new points, especially when one of the points from the table won’t fit on your graph. `(16,-2)` is off the graph. Because you know the square root of `4`, try `x=-3/2`: `(1/4)^(-3/2)=(4/1)^(3/2)=4^(3/2)=(sqrt4)^3=2^3=8`

The point `(8,-3/2)` has been included in blue. You may not feel it necessary to include additional points. You also may need to use a calculator, depending on the base.

Answer

Connect the points as best you can, using a smooth curve.

If the base is less than `1`, the logarithmic function is decreasing. The graph gets close to the `y`-axis when `x` is small, but with positive `y` values instead of negative ones.

As you’ve seen, there are three essential quantities in a logarithmic equation `y = log_b x`: the base `b`, the exponent `y`, and the input `x`. Any of these could be missing in an equation you need to solve. Often the easiest way to solve these is to convert the logarithmic equation to an exponential equation.

Example
Problem	Solve `4 = log_5 x`.
	`4 = log_5 x` means `5^4 = x`	Convert the logarithmic equation to an exponential equation.
	`5^4 = 5 * 5 * 5 * 5` `5^4 = 25 * 25` `5^4 = 625`	In this case, you only need to evaluate `5^4` to solve for `x`.
Answer	`x=625`

When solving for `b` or `y`, it’s helpful to know a lot of exponential relationships, such as `5^3 = 125` and `2^5 = 32`, off the top of your head. However, even if you don’t, you can do some thinking to approximate, or even find exactly, the solutions.

Example
Problem	Solve `3 = log_b 64`.
	`3 = log_b 64` means `b^3 = 64`	Convert the logarithmic equation to an exponential equation.
		You may not know what number to the third power is `64`. You can try a few and zero in on it quickly, though.
	`1^3 = 1` `10^3 = 1,000`	`1^3` and `10^3` are easy to calculate, so let’s start there. `64` is much closer to `1` than to `1,000`, so the correct base will be closer to `1` than to `10`.
		Let’s try some other low values. Since `64` is even, you know you don’t need to try any odd numbers. An odd number to any power will always be odd, and an even number to any power will always be even.
	`2^3 = 8` `4^3 = 4 * 16 = 64`	So let’s try `2` and `4`.
Answer	`b = 4`	Found it! Be sure you are providing the correct number for your answer. It would be easy to mistakenly answer “`64`” here!

Example

Problem

Solve `y = log_5 125`.

`y = log_5 125` means `5^y=125`

Convert the logarithmic equation to an exponential equation.

`y`	`5^y`
`1`	`5`
`2`	`25`
`3`	`125`

What power of `5` is `125`? You might know, but if you don’t, make a table of values for `y` and `5^y`. Look for `125`, or close to it, in the `5^y` column.

Answer

`y=3`

Again, be sure you provide the correct number. It would be easy to make a mistake and write `125` here!

Logarithmic functions are closely related to exponential equations. In fact, `log_b x=y`says the same thing as `b^y=x`. The graphs look similar, but with characteristics such as the domain and range switched between the `x` values and the `y` values. Converting a logarithmic equation to the equivalent exponential equation is helpful with both graphing and solving equations.

Logarithmic Form	Exponential Form
`log_2 16=4`	`2^4 = 16`
`log_7 1=0`	`7^0 = 1`
`log_5 5=1`	`5^1 = 5`
`log_4(1/4)=-1`	`4^-1=1/4`
`log_10 0.01=log_10(1/100)=-2`	`10^-2=0.01`

Learning Objectives

Introduction

Calculating Exponents

Connecting Exponential and Logarithmic Equations

Graphing Logarithmic Functions

Solving Logarithmic Equations

Summary

Table `1`
Input `x`, an exponent `x`	Output `y` `y=2^x`
`-3`	`1/8`
`-2`	`1/4`
`-1`	`1/2`
`0`	`1`
`1`	`2`
`2`	`4`
`3`	`8`

Table `2`
Input `x`, a number that is a power of `2` `x=2y`	Output `y`, the exponent of `2` `y`
`1/8`	`-3`
`1/4`	`-2`
`1/2`	`-1`
`1`	`0`
`2`	`1`
`4`	`2`
`8`	`3`