Square Roots and Completing the Square

Learning Objectives

• Solve quadratic equations by using the Square Root Property.
• Identify and complete perfect square trinomials.
• Solve quadratic equations by completing the square.

Quadratic equations can be solved in many ways. You may already be familiar with factoring to solve some quadratic equations. However, not all quadratic equations can be factored. In this topic, you will use square roots to learn another way to solve quadratic equations, and this method will work with all quadratic equations.

One way to solve the quadratic equation `x^2 = 9` is to subtract `9` from both sides to get one side equal to `0`: `x^2 - 9 = 0`. The expression on the left can be factored: 

`(x + 3)(x - 3) = 0`. Using the zero factor property, you know this means `x + 3 = 0` or `x - 3 = 0`, so `x = -3` or `3`.

Another property would let you solve that equation more easily.

A shortcut way to write “`sqrta`” or “`-sqrta`” is “`+-sqrta`”. The symbol `+-` is often read “positive or negative.” If it is used as an operation (addition or subtraction), it is read “plus or minus.”

Notice that there is a difference here in solving `x^2 = 9` and finding `sqrt9`. For `x^2 = 9`, you are looking for all numbers whose square is `9`. For `sqrt9`, you only want the principal (nonnegative) square root. The negative of the principal square root is `-sqrt9`; both would be `+-sqrt9`. Unless there is a symbol in front of the radical sign, only the nonnegative value is wanted!

In the example above, you can take the square root of both sides easily because there is only one term on each side. In some equations, you may need to do some work to get the equation in this form. You will find that this involves isolating `x^2`.

Sometimes more than just the `x` is being squared:

This method can be helpful when solving real-world problems.

Of course, quadratic equations often will not come in the format of the examples above. Most of them will have `x` terms. However, you may be able to factor the expression into a squared binomial, and, if not, you can still use squared binomials to help you.

First, let’s consider squared binomials. Some of the above examples have squared binomials: `(1 + r)^2` and `(x - 2)^2` are squared binomials. (They are binomials, two terms, that are squared.) If you expand these, you get a perfect square trinomialA trinomial that is the product of a binomial times itself, such as `a^2 + 2ab + b^2` (from `(a + b)^2)`, and `a^2 - 2ab + b^2` (from `(a - b)^2)`. . For example, `(1 + r)^2 = (1 + r)(1 + r) = 1 + 2r + r^2`, or `r^2 + 2r + 1`. The trinomial `r^2 + 2r + 1` is a perfect square trinomial. Notice that the first and last terms are squares (`r^2` and `1`). The middle term is twice the product of the square roots of the first and last terms, the square roots are `r` and `1`, and the middle term is `2(r)(1)`.

Perfect square trinomials have the form `r^2 + 2rs + s^2` and can be factored as `(r + s)^2`, or they have the form `r^2 - 2rs + s^2` and can be factored as `(r - s)^2`. Let’s factor a perfect square trinomial into a squared binomial.

You can use the procedure in this next example to help you solve equations where you identify perfect square trinomials, even if the equation is not set equal to `0`.

You may have looked at the problem above and thought, “Why not subtract `8` from both sides first, making the equation `4x^2 + 20x + 17 = 0`?” This is one technique for solving for `x`. The problem is that, even if you did this, the equation `4x^2 + 20x + 17 = 0` cannot be factored with real numbers. (Try it. Can you think of two numbers whose product is `68` and whose sum is `20`?)

Since the expression `4x^2 + 20x + 25` can be identified as a perfect square trinomial, it is best to factor it as `(2x + 5)^2` and then use the Square Root Property.

One way to solve quadratic equations is by completing the squareA method for solving quadratic equations by rewriting one side of the equation as a squared binomial.. When you don’t have a perfect square trinomial, you can create one by adding a constant term that is a perfect square to both sides of the equation. Let’s see how to find that constant term.

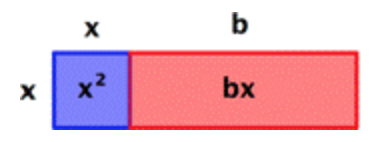
“Completing the square” does exactly what it says: it takes something that is not a square and makes it one. This idea can be illustrated using an area model of the binomial `x^2 + bx`.

`x(x+b)=x^2+bx`

In this example, the area of the overall rectangle is given by `x(x + b)`.

Now let's make this rectangle into a square. First, divide the red rectangle with area `bx` into two equal rectangles each with area `b/2x` . Then rotate and reposition one of them. You haven't changed the size of the red area; it still adds up to `bx`.

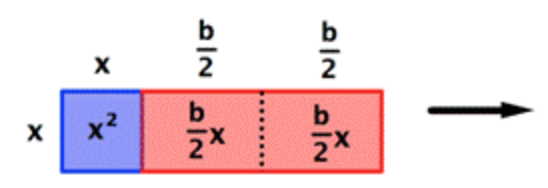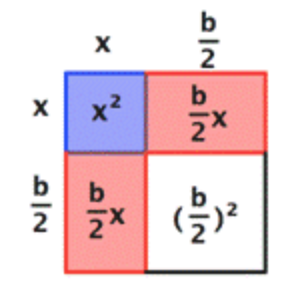`x^2+2(b/2)x+(b/2)^2`

The red rectangles now make up two sides of a square, shown in white. The area of that square is the length of the red rectangles squared, or `(b/2)^2`.

Here comes the cool part: when the white square is added to the blue and red regions, the whole shape is also now a square. In other words, you've “completed the square!” By adding the quantity `(b/2)^2` to the original binomial, you've made a square, a square with sides of `x+b/2`.

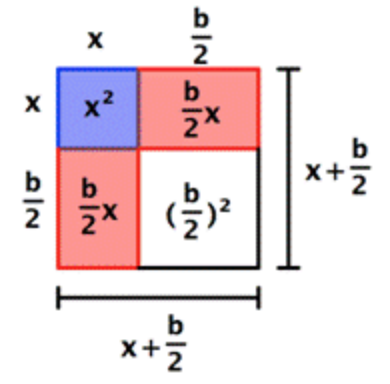`x^2+bx+(b/2)^2=x^2+2(b/2)x+(b/2)^2=(x+b/2)^2`

Notice that the area of this square can be written as a squared binomial: `(x+b/2)^2`.

Notice that `(b/2)^2` is always positive, since it is the square of a number. When you complete the square, you are always adding a positive value.

You can use completing the square to help you solve a quadratic equation that cannot be solved by factoring.

Let’s start by seeing what happens when you complete the square in an equation. In the example below, notice that completing the square will result in adding a number to both sides of the equation. You have to do this in order to keep both sides equal!

Can you see that completing the square in an equation is very similar to completing the square in an expression? The main difference is that you have to add the new number (`+9` in this case) to both sides of the equation to maintain equality.

Now let’s look at an example where you are using completing the square to actually solve an equation, finding a value for the variable.

You may have noticed that because you have to use both square roots, all the examples have two solutions. Here is another example that’s slightly different.

Take a closer look at this problem and you may see something familiar. Instead of completing the square, try adding `47` to both sides in the equation. The equation `x^2 + 16x + 17 = -47` becomes `x^2 + 16x + 64 = 0`. Can you factor this equation using grouping? (Think of two numbers whose product is `64` and whose sum is `16`).

It can be factored as `(x + 8)(x + 8) = 0`, of course! Knowing how to complete the square is very helpful, but it is not always the only way to solve an equation.

Completing the square is used to change a binomial of the form `x^2 + bx` into a perfect square trinomial `x^2+bx+(b/2)^2`, which can be factored to `(x+b/2)^2`. When solving quadratic equations by completing the square, be careful to add `(b/2)^2` to both sides of the equation to maintain equality. The Square Root Property can then be used to solve for `x`. With the Square Root Property, be careful to include both the principal square root and its opposite. Be sure to simplify as needed.