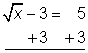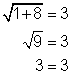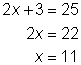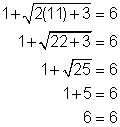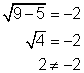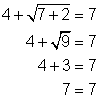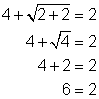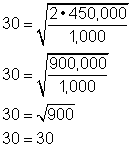Resolviendo ecuaciones radicales

 

Objetivos de aprendizaje

·         Resolver ecuaciones que contienen radicales.

·         Reconocer soluciones extrañas.

·         Resolver problemas de aplicación que involucran ecuaciones radicales como parte de la solución.

 

 

Una ecuación que contiene una expresión radical se llama ecuación radical. Resolver ecuaciones radicales requiere aplicar las reglas de los exponentes y seguir algunos principios algebraicos básicos. En algunos casos, también requiere buscar errores generados por elevar a una potencia par cantidades desconocidas.

 

 

Una estrategia básica para resolver ecuaciones radicales es despejar primero el término racional y luego elevar a una potencia ambos lados de la ecuación para eliminar el radical. (La razón por la que usamos potencias será más clara en un momento) Este es el mismo tiempo de estrategia que usaste para resolver otras ecuaciones sin radicales, reordenar la expresión para despejar la variable que quieres conocer y luego resolver la ecuación resultante.

 

Hay dos ideas claves que usarás para resolver ecuaciones radicales, la primera es que si , entonces . (Esta propiedad te permite elevar al cuadrado ambos lados de una ecuación y estar seguro que los dos lados siguen siendo iguales.) La segunda es que si una raíz cuadrada de un número no negativo x se eleva al cuadrado, entonces obtienes x: . (Esta propiedad te permite “eliminar” los radicales de tus ecuaciones.)

 

Empecemos con una ecuación radical que puedes resolver en pocos pasos: .

 

 

 

 

Para comprobar tu solución, puedes sustituir 64 por x en la ecuación original. ¿Es ? Sí, la raíz cuadrada de 64 es 8 y 8 − 3 = 5.

 

Observa cómo combinaste los términos semejantes y luego elevaste al cuadrado ambos lados de la ecuación. Este es el método estándar para eliminar un radical de una ecuación. Es importante despejar el radical a un lado de la ecuación y simplificar lo más posible antes de elevar al cuadrado. Entre menos términos haya antes de elevar al cuadrado, menos términos adicionales se generarán por el proceso.

 

En el ejemplo anterior, sólo la variable x estaba dentro del radical. Algunas veces necesitarás resolver una ecuación que contiene varios términos dentro de un radical. Sigue los mismos pasos para resolverlas, pero pon atención en un punto crítico, eleva al cuadrado ambos lados de la ecuación, no términos individuales. Observa cómo se resuelven los siguientes dos problemas.

 

 

 

 

 

 

Resolviendo ecuaciones radicales   Sigue los siguientes cuatro pasos para resolver ecuaciones radicales.   1.      Despejar la expresión racional. 2.      Elevar al cuadrado ambos lados de la ecuación: Si x = y entonces x2 = y2. 3.      Una vez eliminado el radical, resuelve la incógnita. 4.      Comprueba todas las respuestas.

 

 

Resolver.   A) B) C) D)   Mostrar/Ocultar Respuesta A) Incorrecto. Comprueba tu respuesta. Si sustituyes  en la ecuación, obtienes , o . Esto no es correcto. Recuerda elevar al cuadrado ambos lados para resolver x. La respuesta correcta es .   B) Incorrecto. Parece que elevaste al cuadrado ambos lados pero ignoraste el +22 dentro del radical. Recuerda incluir todo el binomio cuando eleves al cuadrado ambos lados; luego resuelve x. La respuesta correcta es .   C) Correcto. Elevando al cuadrado ambos lados, encuentras que  se vuelve , entonces  y .   D) Incorrecto. Parece que sólo elevaste al cuadrado la parte izquierda de la ecuación. Recuerda incluir todo el binomio cuando eleves al cuadrado ambos lados: , que se vuelve . Ahora resuelve x. La respuesta correcta es .

 

 

 

Seguir las reglas es importante, pero también lo es poner atención a las matemáticas que tienes enfrente, especialmente cuando resuelves ecuaciones radicales. Observa el siguiente problema que demuestra un error potencial de elevar ambos lados para eliminar un radical.

 

 

 

 

Mira eso, la respuesta a = 9 no produce un enunciado válido cuando se sustituye en la ecuación original. ¿Qué paso?

 

Comprueba el problema original: . Observa que el radical es igual a −2 y recuerda que la raíz cuadrada principal de un número sólo puede ser positiva. ¡Esto significa que ningún valor de a resultará en una expresión radical cuya raíz cuadrada se −2! Habrás notado inmediatamente y concluido que no había soluciones para a. Pero ¿por qué el proceso de elevar al cuadrado produjo una respuesta, a = 9, que fue incorrecta?

 

La respuesta está en el proceso mismo de elevar al cuadrado. Cuando elevas un número a una potencia par, ya sea segunda, cuarta, o 50^va, puedes introducir una falsa solución porque el resultado de una potencia par siempre es un número positivo. Piensa en esto: 3² y (−3)² ambos son 9 y 2⁴ y (−2)⁴ ambos son 16. Entonces cuando elevaste al cuadrado −2 y obtuviste 4 en este problema, artificialmente convertiste la cantidad a positiva. Esta es la razón por la que encontraste un valor para a, ¡resolviste el problema como si estuvieras resolviendo ! (La solución correcta de  en realidad es “no hay solución.”)

 

Valores incorrectos de la variable, como aquellos introducidos como resultado del proceso de elevar al cuadrado se llaman soluciones extrañas. Las soluciones extrañas aparentan una solución real, pero puedes identificarlas porque no crean un enunciado válido cuando se sustituyen en la ecuación original. Esta es una de las razones por las que es importante comprobar tu trabajo, si no compruebas tus respuestas sustituyéndolas en la ecuación original, podrías introducir soluciones extrañas en el problema.

 

Observa el siguiente problema. Observa cómo el problema original es , pero después de elevar al cuadrado ambos lados, se vuelve . Elevar al cuadrado ambos lados puede introducir soluciones extrañas.

 

 

 

 

Podría ser difícil entender por qué existen soluciones extrañas. Considerar las soluciones extrañas graficando la ecuación podría ayudar a entender lo que está sucediendo.

 

Puedes graficar  en el plano de coordenadas dividiéndola en un sistema de dos ecuaciones:  y . La gráfica se muestra abajo. Observa cómo las dos gráficas se intersectan en un punto, cuando el valor de x es −1. Este es el valor de x que satisface ambas ecuaciones, por lo que es la solución del sistema.

 

 

Ahora, siguiendo el trabajo que hiciste en el problema de ejemplo, elevemos al cuadrado ambas expresiones para eliminar la variable del radical. En lugar de resolver la ecuación ahora resolveremos la ecuación, o . Las gráficas de  y  están graficadas abajo. Observa cómo las dos gráficas se intersectan en dos puntos, cuando los valores de x son −1 y −6.

 

Aunque se muestra x = −1 como una solución de ambas gráficas, elevar al cuadrado ambos lados de la ecuación ha dejado el efecto de una solución extraña, x = −6. De nuevo, ¡es por esto que es importante comprobar tus soluciones cuando resuelves ecuaciones radicales!

 

 

 

 

Resolver.   A) x = 3, 0 B) x = 0, 10 C) x = 0 D) x = 10   Mostrar/Ocultar Respuesta A) x = 3, 0 Incorrecto. Para resolver la ecuación, eleva al cuadrado ambos lados y luego resuelve la ecuación resultante: . La respuesta correcta es x = 10.   B) x = 0, 10 Incorrecto. Parece que resolviste la ecuación  correctamente, pero olvidaste elevar al cuadrado ambos lados por x en la ecuación original. ¡x = 0 es una solución extraña porque no vuelve válida la ecuación original! La respuesta correcta es x = 10.   C) x = 0 Incorrecto. Cuando elevas al cuadrado ambos lados y luego resuelves la ecuación resultante, , obtienes x = 0 como una posible solución. Sin embargo, ¡x = 0 es una solución extraña porque no vuelve válida la ecuación original! La respuesta correcta es x = 10.   D) x = 10 Correcto. Al resolver la ecuación, encontraste que elevar al cuadrado los dos lados resulta en , que se simplifica a . Si bien esta ecuación produce valores de x de 0 o 10, 0 es extraña porque no vuelve válida la ecuación original.

 

 

 

Las ecuaciones radicales juegan un rol importante en la ciencia, la ingeniería e incluso la música. Algunas veces podrás necesitar lo que sabes sobre ecuaciones radicales para resolver variables diferentes en este tipo de problemas.

 

 

 

 

 

Un método común para resolver ecuaciones radicales es elevar al cuadrado ambos lados de la ecuación a una potencia que elimine el signo radical de la ecuación. Pero ten cuidado, cuando se elevan al cuadrado ambos lados de la ecuación a una potencia par, existe la posibilidad de introducir soluciones extrañas. Cuando resuelves una ecuación radical, es importante comprobar tu respuesta sustituyendo el valor en la ecuación original. Si obtienes un enunciado válido, entonces ese valor es la solución; si obtienes un enunciado inválido, entonces no es una solución.