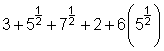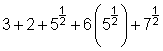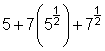Sumando y restando radicales

 

Objetivos de aprendizaje

·         Sumar radicales y simplificar.

·         Restar radicales y simplificar.

 

 

Existen dos principios para combinar radicales sumando y restando: el índice y el radicando. Si son los mismos, la suma y la resta son posibles. Si no, entonces no puedes combinar dos radicales.

 

Entender una cadena de radicales podría ser difícil. Un consejo útil es pensar en los radicales como variables y tratarlos de la misma manera. Empecemos con eso.

 

 

Los radicales pueden parecer confusos cuando se presentan como una cadena larga, como en . ¿Cómo simplificas esta expresión? (Vale la pena mencionar que normalmente no verás radicales presentados en esta forma... ¡pero es una manera útil para aprender a sumar y restar radicales!)

 

Tratar radicales de la misma manera que tratar variables es una buena forma de comenzar. Por ejemplo, no tendrías problemas simplificando la expresión siguiente.

 

 

Combinando los términos semejantes, puedes encontrar rápidamente que 3 + 2 = 5 y a + 6a = 7a. La expresión se puede simplificar como 5 + 7a + b.

 

Lo mismo sucede con los radicales. Siempre y cuando los radicales tengan el mismo radicando (la expresión dentro del signo radical) y el índice (raíz), pueden ser combinados. Abajo, se evalúan las dos expresiones lado a lado.

 

 

Aquí hay otra manera de pensar en esto. Recuerda que los radicales son sólo una alternativa de escribir exponentes fraccionales. Entonces, por ejemplo , y . Si piensas en los radicales en términos de exponentes, entonces aplican todas las reglas de los exponentes.

 

Observa las expresiones abajo. A la izquierda, la expresión está escrita en términos de radicales. A la derecha, la expresión está escrita en términos de exponentes.

 

 

¿Y esto qué significa? Bueno, lo importante es que si necesitas combinar radicales sumando o restando, asegúrate de que tengan el mismo radicando y la misma raíz. Y si las cosas se ponen confusas, o si sólo quieres verificar que estás combinando correctamente, puedes usar lo que sabes sobre las variables y las reglas de los exponentes.

 

 

Veamos algunos ejemplos. En el primer ejemplo, ambos radicales tienen la misma raíz e índice.

 

 

 

 

El siguiente ejemplo contiene más sumandos. Observa cómo puedes combinar los términos semejantes (radicales que tienen la misma raíz e índice) pero no puedes combinar los términos distintos.

 

 

 

 

Observa que la expresión en el ejemplo anterior se simplifica aunque tiente dos términos:  y . ¡Sería un error intentar combinarla más! (Algunas personas cometen el error de . Esto es incorrecto porque  y  no son radicales similares por lo que no se pueden sumar.)

 

 

 

 

Algunas veces podrías necesitar sumar y simplificar un radical. Si los radicales son diferentes, intenta primero simplificar, podría ser que combines los radicales al final, como se muestra en los dos ejemplos siguientes.

 

 

 

 

 

 

Sumar.   A) B) C) D)   Mostrar/Ocultar Respuesta A) Correcto. Cuando sumas expresiones radicales, puedes combinar los radicales similares del mismo modo que sumarías variables similares. .   B) Incorrecto. Revertiste los coeficientes y los radicales. La respuesta correcta es .   C) Incorrecto. Recuerda que no puedes sumar radicales que tienen distintos índices o radicandos. Identifica los radicales semejantes en la expresión e intenta de nuevo. La respuesta correcta es .   D) Incorrecto. Recuerda que no puedes sumar radicales que tienen distintos índices o radicandos. Identifica los radicales semejantes en la expresión e intenta de nuevo. La respuesta correcta es .

 

 

 

La resta de radicales sigue las mismas reglas y métodos que la suma, los radicales e índices deben ser iguales para que dos (o más) radicales puedan ser restados. En los tres ejemplos siguientes, la resta ha sido reescrita como la suma del opuesto.

 

 

 

 

 

 

 

 

Restar y simplificar.   A) B) C) D)   Mostrar/Ocultar Respuesta A) Incorrecto. Para simplificar, puedes reescribir  como . Luego sacar las raíces cuadradas para obtener  La respuesta correcta es .   B) Incorrecto. Recuerda que no puedes combinar dos radicandos a menos que sean iguales., pero . La respuesta correcta es .   C) Correcto. Reescribiendo  como , encontraste que .   D) Incorrecto. Para simplificar, puedes reescribir  como . Luego sacar las raíces cuadradas para obtener  La respuesta correcta es .

 

 

 

Es posible combinar radicales cuando el índice y el radicando de dos o más radicales son iguales. A los radicales con el mismo índice y radicando se les conoce como radicales semejantes. Es útil tratar a los radicales de la misma forma que a las variables: los radicales similares pueden sumarse y restarse de la misma manera que las variables. Algunas veces, necesitarás simplificar una expresión radical antes de que sea posible sumar o restar términos semejantes.