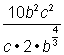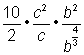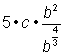Exponentes racionales

 

Objetivos de aprendizaje

·         Convertir radicales a expresiones con exponentes racionales.

·         Convertir expresiones con exponentes racionales a su equivalente radical.

·         Usar las reglas de los exponentes para simplificar expresiones con exponentes racionales.

·         Usar exponentes racionales para simplificar expresiones radicales.

Las raíces cuadradas se escriben comúnmente usando el signo radical, así, . Pero hay otra manera de representar una raíz. Puedes usar exponentes racionales en lugar de un radical. Un exponente racional es un exponente que es una fracción. Por ejemplo,  puede escribirse como .

 

¿No puedes imaginarte elevando un número a un exponente racional? Puede ser difícil acostumbrarse a ellos, pero los exponentes racionales pueden ayudar a simplificar algunos problemas. Exploremos la relación entre los exponentes racionales (fraccionales) y los radicales.

 

 

Los radicales y los exponentes fraccionales son maneras alternativas de expresar lo mismo. Ya has visto cómo las raíces cuadradas pueden expresarse como un exponente a la potencia de un medio.

 

 

Veamos otros ejemplos, pero esta vez con raíces cúbicas. Recuerda, elevar al cubo un número es tener una potencia de tres. Observa que en estos ejemplos el denominador del exponente racional es el número 3.

 

 

Estos ejemplos nos ayudan a modelar la relación entre radicales y exponentes racionales: a saber que la n-ésima raíz de un número puede escribirse como  o .

 

 

Cuando nos encontramos con una expresión que contiene un exponente racional, puedes reescribirla usando un radical. En el ejemplo anterior, observa cómo el denominador del exponente racional determina el índice de la raíz. Entonces, un exponente de  se traduce a una raíz cuadrada, un exponente de  se traduce en una raíz quinta o y  se traduce en una raíz octava .

 

 

 

 

 

 

Recuerda que los exponentes sólo se refieren a la cantidad inmediatamente a la izquierda a menos que haya un símbolo de agrupación. El ejemplo siguiente se ve muy similar al ejemplo anterior con una diferencia importante — !no hay paréntesis! Veamos lo que pasa.

 

 

 

 

 

Así como puedes reescribir una expresión con un exponente racional como una expresión radical, puedes expresar una expresión radical usando un exponente racional.

 

 

 

 

 

 

 

Todos los numeradores para los exponentes racionales en los ejemplos anteriores han sido 1. Puedes usar exponentes fraccionales que tengan numeradores distintos de 1 para expresar raíces, como se muestra a continuación. ¿Notas los patrones en esta tabla?

 

 

Para reescribir un radical usando exponentes fraccionales, la potencia a la que el radicando se eleva se vuelve el numerador y la raíz se vuelve el denominador.

 

Escribiendo exponentes fraccionales   Cualquier radical en la forma  puede escribirse usando un exponente fraccional en la forma .

 

La relación entre y  también funciona para exponentes racionales que tienen un numerador de 1. Por ejemplo, el radical  también se puede escribir como , porque cualquier número conserva su valor si está elevado a la primera potencia. Ahora puedes ver de dónde viene el numerador de 1 de la forma equivalente de .

 

 

Exploremos algunas expresiones radicales para ver cómo simplificarlas. Aquí hay una expresión radical que necesita ser simplificada, .

 

Un método para simplificar esta expresión es factorizar y sacar grupos de a³, como se muestra en el siguiente ejemplo.

 

 

 

 

También puedes simplificar esta expresión pensando en el radical como una expresión con un exponente racional y usando el principio de que cualquier radical en la forma  puede escribirse como un exponente fraccional en la forma .

 

 

 

 

Observa que los exponentes racionales están sujetos a las mismas reglas que otros exponentes cuando aparecen en expresiones algebraicas.

 

Ambos métodos de simplificación nos dieron el mismo resultado, a². Dependiendo del contexto del problema, podría ser más fácil usar un método que el otro, pero por ahora, notarás que pudiste simplificar esta expresión más rápido usando exponentes racionales que usando el método de “sacar”.

 

Intentemos otro ejemplo.

 

 

 

 

De nuevo, el método alternativo consiste en simplificar dentro del radical usando factorización. Para el ejemplo que ya resolviste, se ve así.

 

 

 

 

¿Cuál de las expresiones siguientes es igual a la expresión  cuando se escribe usando un exponente racional?   A)   B)   C)   D)   Mostrar/Ocultar Respuesta A) Incorrecto. El problema pide una expresión con exponentes racionales, o fraccionales. Esta respuesta es para simplificar la expresión radical. La respuesta correcta es .   B) Correcto. Obtener la raíz cuadrada es lo mismo que elevar la cantidad dentro del radical a la potencia .   C) Incorrecto. Esta cantidad es el radicando — la expresión dentro del signo radical. Obtener la raíz cuadrada es lo mismo que elevar la cantidad dentro del radical a la potencia . La respuesta correcta es .   D) Incorrecto. Como 25 también está dentro del símbolo radical, debes elevarlo a la potencia . La respuesta correcta es .

 

 

Intentemos con una expresión más complicada, . Esta expresión tiene dos variables, una fracción y un radical. Vayamos paso a paso para ver si usando exponentes fraccionales nos pueden ayudar a simplificarla.

 

Empecemos con simplificar el denominador, porque es ahí donde está el signo radical.

 

 

 

 

Bueno, esto tomó bastante tiempo, pero lo lograste. Aplicaste lo que sabías sobre exponentes racionales, exponentes negativos y otras reglas de los exponentes para simplificar la expresión.

 

 

Un radical puede expresarse como una expresión con un exponente fraccional siguiendo la convención . Reescribir radicales usando exponentes fraccionales puede ser útil para simplificar algunas expresiones radicales. Cuando trabajes con exponentes fraccionales, recuerda que están sujetos a todas las reglas de los exponentes cuando aparecen en expresiones algebraicas.