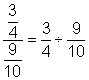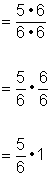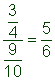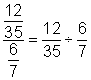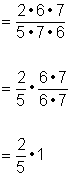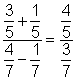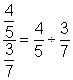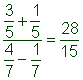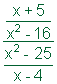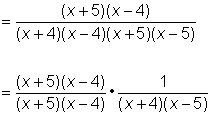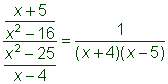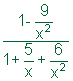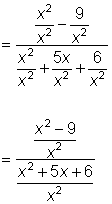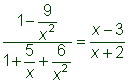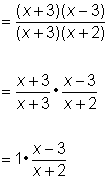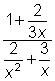Expresiones racionales complejas
Objetivo de aprendizaje
· Simplificar expresiones racionales complejas.
Introducción
Las fracciones y las expresiones racionales pueden interpretarse como cocientes. Cuando el dividendo (numerador) y el divisor (denominador) incluyen fracciones o expresiones racionales, tienes algo un poco más complejo que lo normal. No te preocupes, ¡tienes las herramientas necesarias para simplificar estos cocientes!
Fracciones complejas
Una fracción compleja es el cociente de dos fracciones. Estas fracciones complejas nunca se consideran como una forma simple, pero siempre pueden simplificarse usando división o fracciones.
| Ejemplo | ||
| Problema | Simplificar.
|
|
|
|
| Reescribe la fracción compleja como un problema de división. |
|
|
| Reescribe la división como una multiplicación, usando el recíproco del divisor. |
|
|
| Multiplica y simplifica si es posible. |
| Respuesta |
|
|
Antes de que multipliques los números, normalmente es útil factorizar los números. Entonces puedes usar los factores para crear una fracción igual a 1.
| Ejemplo | ||
| Problema | Simplificar.
|
|
|
|
| Reescribe la fracción compleja como un problema de división. |
|
|
| Reescribe la división como una multiplicación, usando el recíproco del divisor. |
|
|
| Factoriza el numerador y el denominador, buscando factores comunes, antes de multiplicar los números. |
| Respuesta |
|
|
Si dos fracciones aparecen en el numerador o el denominador (o ambos), primero combínalas. Luego simplifica el cociente como se muestra a continuación.
| Ejemplo | ||
| Problema | Simplificar.
|
|
|
|
| Primero combina el numerador y el denominador sumando o restando. |
|
|
| Reescribe la fracción compleja como un problema de división. |
|
|
| Reescribe la división como una multiplicación, usando el recíproco del divisor. |
|
|
| Multiplica y simplifica si es posible. |
| Respuesta |
|
|
| Simplificar.
A)
B)
C)
D)
|
por 
en lugar de dividir. La fracción compleja es equivalente a 
, que es 
. La respuesta correcta es 
Una expresión racional compleja es un cociente con expresiones racionales en el dividendo, en el divisor, o ambos. Simplifícalas de la misma manera que lo harías con una fracción compleja.
| Ejemplo | ||
| Problema | Simplificar.
|
|
|
|
| Reescribe la expresión racional compleja como un problema de división. |
|
|
| Reescribe la división como una multiplicación, usando el recíproco del divisor. Observa que los valores excluidos son -4, 4 y 5, porque esos valores hacen cero los denominadores una de las fracciones. |
|
|
| Factoriza el numerador y el denominador, buscando factores comunes. En este caso, x + 5 y x – 4 son factores comunes del numerador y del denominador. Observa que |
| Respuesta |
|
|
es igual a 1.
Las mismas ideas pueden ser usadas cuando simplificas expresiones racionales complejas que incluyen más de una expresión racional en el numerador o en el denominador. Sin embargo, hay un atajo que puedes usar. Compara los siguientes dos ejemplos de simplificación de una fracción compleja.
| Ejemplo | ||
| Problema | Simplificar.
|
|
|
| Combina las expresiones en el numerador y en el denominador. Para hacer esto, reescribe las expresiones usando un común denominador. Hay un valor excluido de 0 porque hace que los denominadores de las fracciones san cero. | |
|
| Reescribe la expresión racional compleja como un problema de división. (Cuando dudes con este paso de reescribir la fracción racional compleja, podrías brincártelo y pasar directamente a reescribirla como una multiplicación.) | |
|
| Reescribe la división como una multiplicación, usando el recíproco del divisor. | |
|
| Factoriza el numerador y el denominador, buscando factores comunes. En este caso, x + 3 y x2 son factores comunes. Ahora podemos ver que hay dos valores excluidos adicionales, -2 y -3. | |
| Respuesta |
|
|
| Ejemplo | ||
| Problema | Simplificar.
|
|
|
|
| Antes de combinar las expresiones, encuentra el común denominador para todas las expresiones racionales. (En este caso, x2 es un común denominador.) Multiplica por 1 en la forma de fracción con el común denominador en el numerador y el denominador. (En este caso, multiplica por |
|
|
| ¡Observa que la expresión ya no es compleja! Puedes simplificar factorizando e identificando factores comunes. Ahora podemos ver que hay dos valores excluidos adicionales, -2 y -3. |
| Respuesta |
|
|
Puede que el segundo método te parezca más fácil. Intenta con ambos métodos en el siguiente problema.
| Simplificar.
A) 1
B)
C)
D)
|
. Multiplicando la expresión por
Sumario
Las expresiones racionales complejas son cocientes con expresiones racionales en el divisor, en el dividendo, o en ambos. Cuando se escriben en forma fraccional, parecen fracciones dentro de fracciones. Esto puede simplificarse tratando el cociente como un problema de división. Luego puedes reescribir la división como una multiplicación usando el recíproco del divisor. O puedes simplificar la expresión racional compleja multiplicando el numerador y el denominador por un común denominador con todas las expresiones racionales en la expresión compleja. Esto puede ay darte a simplificar una expresión compleja más rápido.
