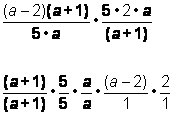Multiplicando y dividiendo expresiones racionales

 

Objetivos de aprendizaje

·         Multiplicar y simplificar expresiones racionales.

·         Dividir y simplificar expresiones racionales.

 

 

Así como puedes multiplicar y dividir fracciones, también puedes multiplicar y dividir expresiones racionales. De hecho, usas el mismo proceso para multiplicar y dividir expresiones racionales que el que usas para multiplicar y dividir fracciones numéricas. ¡El proceso es el mismo aunque las expresiones se vean diferentes!

 

 

Recuerda que hay dos maneras de multiplicar fracciones numéricas.

 

Una manera es multiplicar los numeradores y los denominadores y luego simplificar el producto, como se muestra aquí.

 

 

Una segunda manera es factorizar y simplificar las fracciones antes de realizar la multiplicación.

 

 

Observa que ambos métodos resultan en el mismo producto. En algunos casos podrá ser más fácil primero multiplicar y luego simplificar, mentiras que en otros casos tendrá más sentido simplificar las fracciones antes de multiplicar.

 

Los mismos dos métodos pueden aplicarse a las expresiones racionales. En los siguientes ejemplos, se muestran ambas técnicas. Primero, vamos a multiplicar y luego a simplificar.

 

 

 

 

Muy bien, funcionó. Pero esta vez vamos a simplificar primero, luego a multiplicar. Cuando usamos este método, es buena idea encontrar el máximo factor común. Puedes factorizar cualquier factor común, pero encontrar el máximo tomará menos pasos.

 

 

 

 

Ambos métodos producen la misma respuesta.

 

También, recuerda que cuando trabajas con expresiones racionales, debes habituarte a identificar cualquier valor para las variables que resultarían en una división entre 0. Estos valores excluidos deben ser eliminados del dominio, el conjunto de todos los valores posibles de la variable. En el ejemplo anterior, , el dominio es todos los números reales done a es distinta de 0. Cuando a = 0, el denominador de la fracción es igual a 0, que volverá indefinida la fracción.

 

Algunas expresiones racionales contienen expresiones cuadráticas y otros polinomios de varios términos. Para multiplicar estas expresiones racionales, el mejor método es primero factorizar los polinomios y luego buscar factores comunes. (Multiplicar los términos antes de factorizar normalmente crea polinomios complicados ... ¡y luego tendrás también que factorizar estos polinomios! Por esta razón, es más fácil factorizar, simplificar y luego multiplicar.) Sólo sigue un paso a la vez, como en los ejemplos siguientes.

 

 

 

 

 

 

Observa que en la respuesta anterior, no puedes simplificar aún más la expresión racional. Puede ser tentador expresar los 5's en el numerador y el denominador como la fracción , pero estos 5’s son términos porque están siendo sumados o restados. ¡Recuerda que sólo los factores comunes y no los términos, pueden reagruparse para formar factores de 1!

 

 

Multiplica y expresa el producto como una expresión racional simplificada.   y ≠ −8, −2, 0, 2,   A)   B)   C)     D)   Mostrar/Ocultar Respuesta A) Incorrecto. Simplificas factorizando los numeradores y los denominadores. La fracción  puede escribirse como y la fracción  puede escribirse como . La respuesta correcta es .   B) Incorrecto. Esta expresión es equivalente, pero puede simplificarse más porque existe el factor común y en el numerador y el denominador. La respuesta correcta es .   C) Incorrecto. Esta expresión es equivalente, pero puede simplificarse más porque existen factores comunes en el numerador y el denominador: . La respuesta correcta es .   D) Correcto. Factorizando los numeradores y los denominadores, obtienes . Reagrupando, obtienes = .

 

 

 

Hemos visto que podemos multiplicar expresiones racionales del mismo modo que multiplicamos fracciones numéricas. No debería sorprendernos que también dividimos expresiones racionales de la misma forma que dividimos fracciones numéricas. Específicamente, para dividir expresiones racionales, mantienes la primera expresión racional, cambias el signo de división a multiplicación y tomas el recíproco de la segunda expresión racional.

 

Empecemos recordando la división de fracciones numéricas.

 

 

Usa el mismo proceso para dividir expresiones racionales. Puedes pensar en la división como una multiplicación por el recíproco y luego usar lo que sabes sobre la multiplicación para simplificar.

 

Debes tener en cuenta el dominio, específicamente los valores de la variable que harían el denominador igual a cero. Pero esta vez hay una nueva consideración — ya que divides multiplicando por el recíproco de una de las expresiones racionales, también necesitas encontrar los valores que harían el numerador igual a cero. Veamos.

 

 

 

 

Saber encontrar el dominio puede ser poco importante, pero te ayudará cuando aprendas a resolver ecuaciones racionales. Al dividir, multiplica por el recíproco.

 

 

 

 

 

 

Observa que una vez que reescribes la división como una multiplicación por el recíproco, sigues el mismo proceso que usaste al multiplicar expresiones racionales.

 

 

Encuentra el cociente y exprésalo como una expresión racional simplificada.   , el dominio es todos los números reales excepto −2 y −1.   A)   B)   C)   D)   Mostrar/Ocultar Respuesta A) Incorrecto. Esta operación es una división, no una multiplicación. El primer paso en una división es reescribirla como una multiplicación por el recíproco. La respuesta correcta es.   B) Correcto. Dividir es lo mismo que multiplicar por el recíproco, por lo que el problema puede escribirse: .   C)   Incorrecto. Parece que has tomado el recíproco, lo factorizaste correctamente y simplificaste tus factores comunes a 1, obteniendo . Pero necesitas multiplicar los dos numeradores . La respuesta correcta es .   D) Incorrecto. Este es un problema de división. El primer paso en la división es reescribirla como una multiplicación por el recíproco. También simplificaste incorrectamente. La respuesta correcta es .

 

 

 

Las expresiones racionales se multiplican y dividen al igual que las fracciones numéricas. Para multiplicar, primero encuentra los máximos factores comunes del numerador y del denominador. Luego, reagrupa los factores para crear fracciones iguales a uno. Luego, multiplica cualquier factor restante. Para dividir, primero reescribe la división como una multiplicación por el recíproco del denominador. Después, los pasos son los mismos que con la multiplicación.

 

Cuando expresas un producto o un cociente, es importante incluir los valores excluidos. Estos son todos los valores de una variable que harían un denominador igual a cero en cualquiera de los pasos en los cálculos.