Graficando sistemas de desigualdades
Objetivos de Aprendizaje
· Resolver un sistema de desigualdades lineales por medio de una gráfica.
· Determinar si un par ordenado es una solución de un sistema de desigualdades.
· Resolver problemas de aplicación graficando un sistema de desigualdades.
Introducción
Una solución de un sistema de ecuaciones lineales es cualquier par ordenado que sea válido para todas las ecuaciones del sistema. De la misma manera, la solución de un sistema de desigualdades lineales es cualquier par ordenado que sea una solución para todas las desigualdades en el sistema.
Se usan las gráficas para mostrar todas las variables que son soluciones de un sistema de desigualdades lineales.
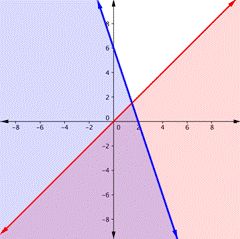
La gráfica de una desigualdad lineal se divide en dos regiones en el plano de coordenadas. En un lado están todas las soluciones de la desigualdad. En el otro lado, no hay soluciones. Considera la gráfica de la desigualdad y < 2x + 5.

La recta punteada es y = 2x + 5. Cada par ordenado en el área sombreada debajo de la recta es una solución de y < 2x + 5, porque todos los puntos debajo de la recta harán válida la desigualdad. Si lo dudas, intenta sustituyendo las coordenadas x y y de los puntos A y B en la desigualdad — verás que funcionan. Entonces, el área sombreada muestra todas las soluciones de la desigualdad.
La recta límite divide el plano en dos mitades, En este caso, se muestra como una recta punteada porque los puntos en la recta no satisfacen la desigualdad. Si la desigualdad hubiera sido y ≤ 2x + 5, entonces la recta límite habría sido sólida.
Grafiquemos otra desigualdad: y > −x. Puedes revisar un par de puntos para determinar qué lado de la recta límite sombrear. Prueba si los puntos M y N hacen enunciados válidos. Entonces, sombreamos el área por encima de la recta. La recta es punteada porque los puntos en ella son inválidos.

Para crear un sistema de desigualdades, necesitas graficar dos o más desigualdades. Usemos y < 2x + 5 y y > −x porque ya tenemos su gráfica.

El área púrpura muestra dónde se traslapan las soluciones de las dos desigualdades. Esta área es la solución del sistema de desigualdades. Cualquier punto dentro de esta región púrpura será válido para y > −x y para y < 2x + 5.
En la gráfica, puedes ver que los puntos B y N son soluciones del sistema porque sus coordenadas hacen válidas ambos enunciados.
En contraste, los puntos M y A están fuera de la región solución (púrpura). Si bien el punto M es una solución de la desigualdad y > −x y el punto A es una solución de la desigualdad y < 2x + 5, ningún punto es una solución del sistema.
| Ejemplo | |||
| Problema | ¿Es el punto (2, 1) una solución del sistema x + y > 1 y 2x + y < 8? | ||
|
| x + y > 1 2 + 1 > 1 3 > 1
VÁLIDO (2, 1) es una solución de x + y > 1. | 2x + y < 8 2(2) + 1 < 8 4 + 1 < 8 5 < 8
VÁLIDO (2, 1) es una solución de 2x + y < 8. | Comprueba el punto en cada una de las desigualdades. Sustituye 2 por x y 1 por y. ¿Es el punto una solución de ambas desigualdades?
|
| Respuesta | El punto (2, 1) es una solución del sistema x + y > 1 y 2x + y < 8. | Como (2, 1) es una solución de cada desigualdad, también es la solución del sistema. | |
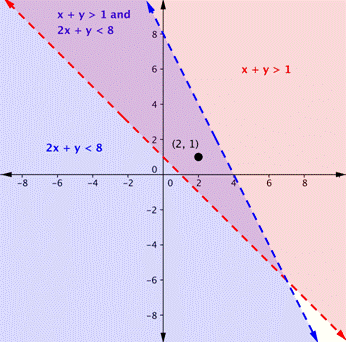
Aquí hay una gráfica del sistema para el ejemplo anterior. Observa que (2, 1) está en el área púrpura, que es el área donde se traslapan las áreas de las dos desigualdades.
| Ejemplo | |||
| Problema | ¿Es el punto (2, 1) una solución del sistema x + y > 1 y 3x + y < 4? | ||
|
| x + y > 1 2 + 1 > 1 3 > 1
VÁLIDO (2, 1) es una solución de x + y > 1. | 3x + y < 4 3(2) + 1 < 4 6 + 1 < 4 7 < 4
INVÁLIDO (2, 1) no es una solución de 3x + y < 4. | Comprueba el punto en cada una de las desigualdades. Sustituye 2 por x y 1 por y. ¿Es el punto una solución de ambas desigualdades?
|
| Respuesta | El punto (2, 1) no es una solución del sistemax + y > 1 y 3x + y < 4. | Como (2, 1) no es una solución de cada desigualdad, no es la solución del sistema. | |
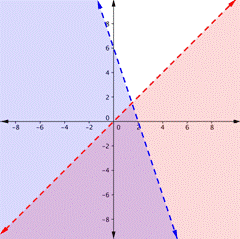
Aquí hay una gráfica para el sistema. Observa que (2, 1) no está en el área púrpura, que es el área de traslape; es una solución para una de las desigualdades (la región roja), pero no es una solución para la otra desigualdad (la región azul).

| ¿Cuáles de los puntos listados son soluciones del sistema? y > x x − 2 < 0
I. (1, 1) II. (−5, 9) III. (0, 7)
A) I y II
B) II y III
C) I y III
D) Sólo II
|
Como se muestra abajo, encontrar soluciones de un sistema de desigualdades puede hacerse graficando cada desigualdad para luego identificar la región que comparten.
| Ejemplo | |||
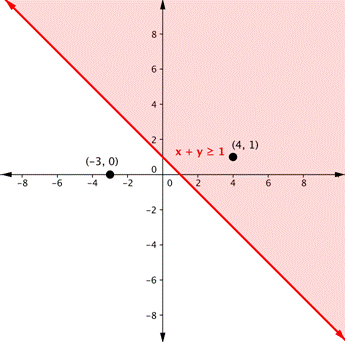
| Problema | Encontrar la solución del sistema x + y ≥ 1 y y – x ≥ 5. | ||
|
| Grafíca una desigualdad. Primero grafica la recta límite usando la tabla de valores, intersecciones, o cualquier otro método que prefieras. La recta límite para x + y ≥ 1 es x + y = 1, o y = −x + 1. Como el signo de igual está incluido con el signo de mayor que, la recta límite es sólida. | ||
|
| Prueba 1: (−3, 0) x + y ≥ 1 −3 + 0 ≥ 1 −3 ≥ 1
INVÁLIDO
| Prueba 2: (4, 1) x + y ≥ 1 4 + 1 ≥ 1 5 ≥ 1
VÁLIDO | Encuentra un par ordenado en algún lado de la recta límite. Inserta los valores de x y y en la desigualdad x + y ≥ 1 y ve qué par ordenado resulta en un enunciado válido. |
|
|
Como (4, 1) resulta en un enunciado válido, la región que incluye (4, 1) debe ser sombreada.
| ||
|
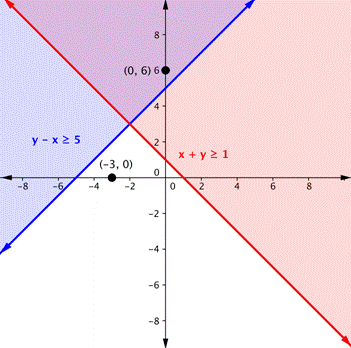
| Haz lo mimo con la segunda desigualdad. Grafica la recta límite, luego prueba puntos para encontrar la región que es solución a la desigualdad. En este caso, la recta límite es y – x = 5 (o y = x + 5) y es sólida. El punto (−3, 0) no es una solución de y – x ≥ 5, pero el punto (0, 6) es una solución. | ||
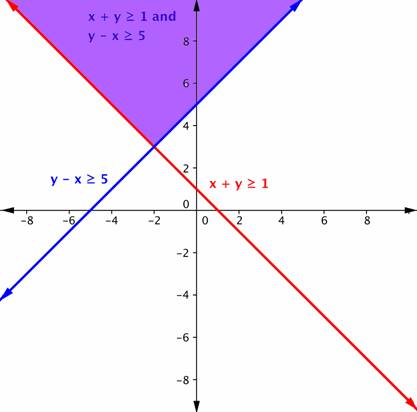
| Respuesta | La región púrpura en esta gráfica muestra el conjunto de todas las soluciones del sistema.
| ||
| Ejemplo | ||
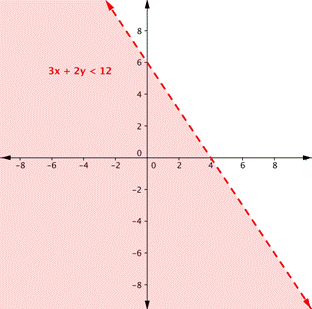
| Problema | Encontrar la solución del sistema 3x + 2y < 12 y −1 ≤ y ≤ 5. | |
|
|
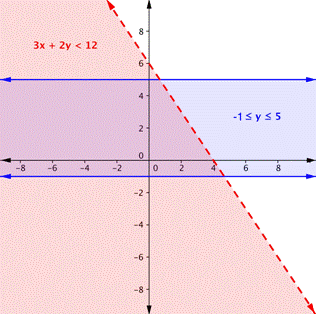
Grafica la desigualdad. Primero grafica la recta límite, luego prueba algunos puntos.
Recuerda, ya que la desigualdad 3x + 2y < 12 no incluye el signo igual, dibuja una recta punteada.
La prueba de un punto (como (0, 0) mostrará que el área debajo de la recta es la solución de la desigualdad. | |
|
|
La desigualdad −1 ≤ y ≤ 5 en realidad son dos desigualdades: −1 ≤ y, y y ≤ 5. Otra manera de pensar en esto es que y debe estar entre −1 y 5. Las rectas son horizontales. La región entre estas dos rectas contiene las soluciones de −1 ≤ y ≤ 5. Hacemos las rectas sólidas porque también queremos incluir y = −1 y y = 5.
Grafíca esta región en el mismo eje que la otra desigualdad. | |
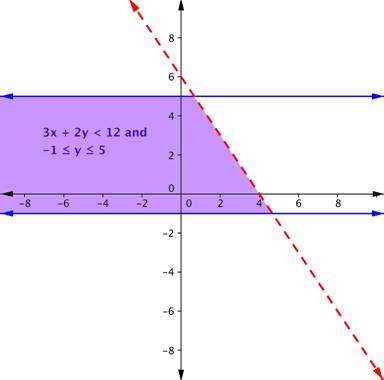
| Respuesta | La región púrpura en esta gráfica muestra el conjunto de todas las soluciones del sistema.
| |
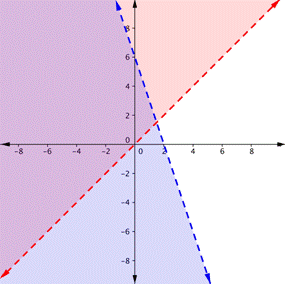
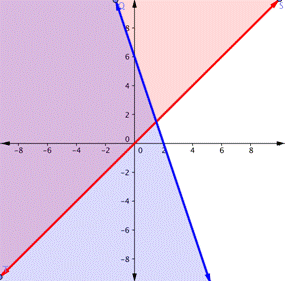
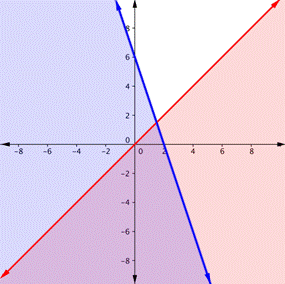
| ¿En cuál de las siguientes regiones púrpuras está la solución del sistema? y > x y < −3x+ 6
A)
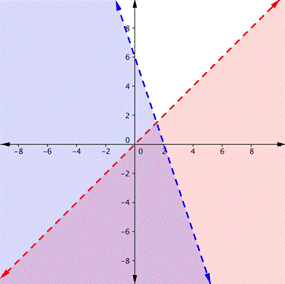
B)
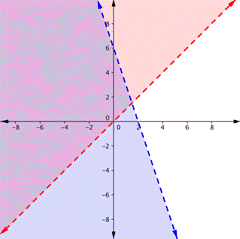
C)
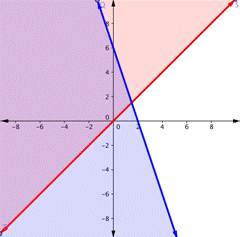
D)
|
Graficar un sistema de desigualdades puede ayudarte a resolver situaciones del mundo real.
| Ejemplo | ||
| Problema | Cathy vende conos de helado para recaudar fondos para su escuela. Vende dos tamaños: chico (con una bola) y grande (con dos bolas). Ella sabe que puede obtener un máximo de 70 bolas de helado de su contenedor. Cobra $3 por un cono chico y $5 por un cono grande.
Cathy quiera ganar por lo menos $120 para dárselos a la escuela. Escribe y grafica un sistema de desigualdades que modelen esta situación. | |
|
| s = cono chico l = cono grande | Primero identifica las variables. Hay dos variables: el número de conos chicos y el número de conos grandes. |
|
| s + 2l ≤ 70 | Escribe la primera ecuación: el número máximo de bolas que puede vender. La cantidad de bolas que tiene disponibles (70) debe ser mayor o igual que el número de bolas para los conos chicos (s) y los conos grandes (2l). |
|
| 3s + 5l ≥ 120 | Escribe la segunda ecuación: la cantidad de dinero que colecta. Ella quiere que el total de ganancia de los conos chicos (3s) y de los conos grandes (5l) sea por lo menos $120. |
|
| s + 2l ≤ 70 3s + 5l ≥ 120 | Escribe el sistema. |
|
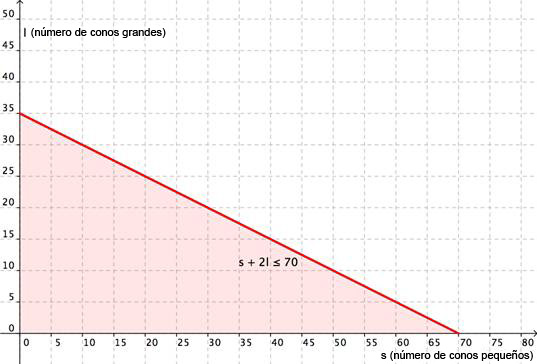
| Ahora grafíca el sistema. Las variables x y y han sido reemplazadas por s y l; grafica s sobre el eje-x, y l sobre el eje-y.
Primero grafíca la región s + 2l ≤ 70. Grafica la recta límite y prueba algunos puntos para ver qué región sombrear. La gráfica se muestra abajo. | |
|
| ||
|
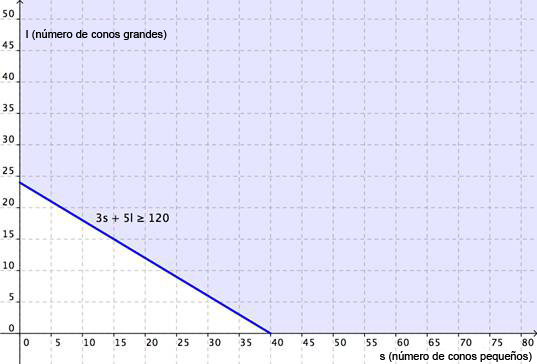
| Ahora grafíca la región 3s + 5l ≥ 120. Grafica la recta límite y prueba algunos puntos para ver qué región sombrear. La gráfica se muestra abajo. | |
|
| ||
|
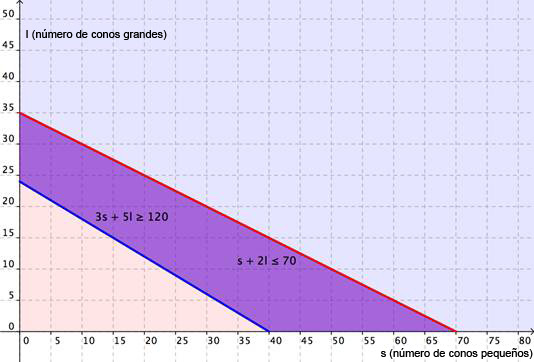
| Graficando ambas regiones, encuentras lo siguiente: | |
|
| ||
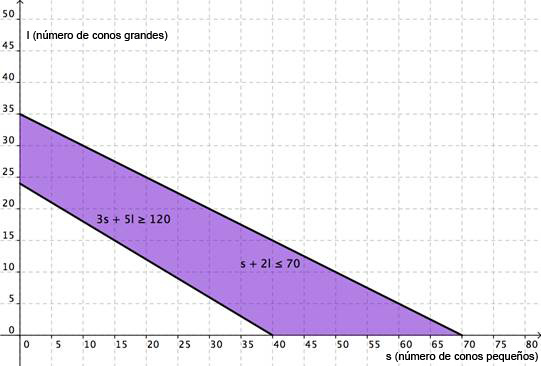
| Y representada como una región traslapada, tienes:
| ||
| Respuesta | La región púrpura es la solución. Siempre y cuando la combinación de conos chicos y conos grandes que vende Cathy pueda mapearse en la región púrpura, ella habrá ganado por lo menos $120 y no habrá usado más de 70 bolas de helado. | |
Sumario
Los sistemas de desigualdades pueden graficarse en el plano de coordenadas. El conjunto solución de un sistema de desigualdades no es un único punto, pero toda una región definida por el traslape de las áreas de cada desigualdad individual en el sistema. Cada punto dentro de esta región es una solución para ambas desigualdades y por lo tanto de todo el sistema.