Graphing Systems of Linear Equations

Learning Objectives

Solve a system of linear equations by graphing.
Determine whether a system of linear equations is consistent or inconsistent.
Determine whether a system of linear equations is dependent or independent.
Determine whether an ordered pair is a solution of a system of equations.
Solve application problems by graphing a system of equations.

Introduction

Recall that a linear equation graphs as a line, which indicates that all of the points on the line are solutions to that linear equation. There are an infinite number of solutions. If you have a system of linear equationsTwo or more linear equations with the same variables., the solution for the system is the value that makes all of the equations true. For two variables and two equations, this is the point where the two graphs intersect. The coordinates of this point will be the solution for the two variables in the two equations.

Systems of Equations

The solution for a system of equations is the value or values that are true for all equations in the system. The graphs of equations within a system can tell you how many solutions exist for that system. Look at the images below. Each shows two lines that make up a system of equations.

One Solution

No Solutions

Infinite Solutions

A coordinate plane shows two lines. A line with a positive slope crosses the x-axis at (negative 1.5, 0) and the y-axis at (0, 1). A line with a negative slope crosses the y-axis at (0, 3) and the x-axis at (3, 0). The lines intersect near (1, 2).

A coordinate plane shows two lines with the same positive slope. The first line crosses the x-axis at (negative 1.5, 0) and the y-axis at (0, 1). The second line crosses the y-axis at (0, negative 2) and the x-axis at (3, 0).

On a coordinate plane, a line has a positive slope. It crosses the x-axis at (negative 1.5, 0) and the y-axis at (0, 1).

If the graphs of the equations intersect, then there is one solution that is true for both equations.

If the graphs of the equations do not intersect (for example, if they are parallel), then there are no solutions that are true for both equations.

If the graphs of the equations are the same, then there are an infinite number of solutions that are true for both equations.

When the lines intersect, the point of intersection is the only point that the two graphs have in common, so the coordinates of that point are the solution for the two variables used in the equations. When the lines are parallel, there are no solutions. Sometimes the two equations will graph as the same line, in which case we have an infinite number of solutions.

Special terms are sometimes used to describe these kinds of systems.

The following terms refer to how many solutions the system has.

When a system has one solution, meaning the graphs of the equations intersect once, the system is a consistent system of linear equationsA system of linear equations that has at least one solution. and the equations are independent.

When a system has no solution, meaning the graphs of the equations don’t intersect at all, the system is an inconsistent system of linear equationsA system of linear equations that has no solutions. and the equations are independent.

If the lines are the same, meaning the graphs intersect at all points, the system is a consistent system of linear equations and the equations are dependent. That is, any solution of one equation must also be a solution of the other, so the equations depend on each other.

The following terms refer to whether the system has any solutions at all.

The system is a consistent system of linear equations when it has solutions.

The system is an inconsistent system of linear equations when it has no solutions.

We can summarize this as follows:

A system with one or more solutions is consistent.
A system with no solutions is inconsistent.
If the lines are different, the equations are independent linear equationsEquations that graph as different straight lines..
If the lines are the same, the equations are dependent linear equationsEquations that graph as the same straight line..

Example
Problem	Using the graph of `y = x` and `x + 2y = 6`, shown below, determine how many solutions the system has. Then classify the system as consistent or inconsistent and the equations as dependent or independent.
		The lines intersect at one point, so the two lines have only one point in common. There is only one solution to the system. Because the lines are not the same, the equations are independent. Because there is only one solution, this system is consistent.
Answer	The system is consistent and the equations are independent.

Advanced Example
Problem	Using the graph of `y = 3.5x + 0.25` and `14x - 4y = -4.5`, shown below, determine how many solutions the system has. Then classify the system as consistent or inconsistent and the equations as dependent or independent.
		The lines are parallel, meaning they do not intersect. There are no solutions to the system. Because the lines are not the same, the equations are independent. There are no solutions. Therefore, this system is inconsistent.
Answer	The system is inconsistent and the equations are independent.

Advanced Question

Which of the following represents dependent equations and consistent systems?

`y=1/2x+5`

`-1/2x+y=-2`

`y=1/5x+5`

`1/5x+y=-3/2`

`y=-3x-1`

`3x+y=-1`

`y=3x-1`

`8x+y=-1`

Show/Hide Answer

Verifying a Solution

From the graph above, you can see that there is one solution to the system `y = x` and `x + 2y = 6`. The solution appears to be `(2, 2)`. However, you must verify an answer that you read from a graph to be sure that it’s not really `(2.001, 2.001)` or `(1.9943, 1.9943)`.

One way of verifying that the point does exist on both lines is to substitute the x- and y-values of the ordered pair into the equation of each line. If the substitution results in a true statement, then you have the correct solution!

Example
Problem	Is `(2, 2)` a solution of the system `y = x` and `x + 2y = 6`?
	`y = x` `2 = 2` TRUE `(2, 2)` is a solution of `y = x`.	`x + 2y = 6` `2 + 2(2) = 6` `2 + 4 = 6` `6 = 6` TRUE `(2, 2)` is a solution of `x + 2y = 6`.	Since the solution of the system must be a solution to all the equations in the system, check the point in each equation. Substitute `2` for `x` and `2` for `y` in each equation.
Answer	`(2, 2)` is a solution to the system.		Since `(2, 2)` is a solution to each of the equations in the system, `(2, 2)` is a solution to the system.

Example
Problem	Is `(3, 9)` a solution of the system `y = 3x` and `2x - y = 6`?
	`y = 3x` `9 = 3(3)` TRUE `(3, 9)` is a solution of `y = 3x`.	`2x - y = 6` `2(3) - 9 = 6` `6 - 9 = 6` `-3 = 6` FALSE `(3, 9)` is not a solution of `2x - y = 6`.	Since the solution of the system must be a solution to all the equations in the system, check the point in each equation. Substitute `3` for `x` and `9` for `y` in each equation.
Answer	`(3, 9)` is not a solution to the system.		Since `(3, 9)` is not a solution of one of the equations in the system, it cannot be a solution to the system.

Example
Problem	Is `(-2, 4)` a solution of the system `y = 2x` and `3x + 2y = 1`?
	`y = 2x` `4 = 2(-2)` `4 = -4` FALSE `(-2, 4)` is not a solution of `y = 2x`.	`3x + 2y = 1` `3(-2) + 2(4) = 1` `-6 + 8 = 1` `2 = 1` FALSE `(-2, 4)` is not a solution of `3x + 2y = 1`.	Since the solution of the system must be a solution to all the equations in the system, check the point in each equation. Substitute `-2` for `x` and `4` for `y` in each equation.
Answer	`(-2, 4)` is not a solution to the system.		Since `(-2, 4)` is not a solution to either of the equations in the system, `(-2, 4)` is not a solution of the system.

Remember that, in order to be a solution to the system of equations, the value of the point must be a solution for both equations. Once you find one equation for which the point is false, you have determined that it is not a solution to the system.

Which of the following statements is true for the system `2x - y = -3` and `y = 4x - 1`?

A) `(2, 7)` is a solution of one equation but not the other, so it is a solution of the system

B) `(2, 7)` is a solution of one equation but not the other, so it is not a solution of the system

C) `(2, 7)` is a solution of both equations, so it is a solution of the system

D) `(2, 7)` is not a solution of either equation, so it is not a solution to the system

Show/Hide Answer

Graphing as a Solution Method

You can solve a system graphically. However, it is important to remember that you must check the solution, as the graph might not be accurate.

Example
Problem	Find all solutions to the system `y - x = 1` and `y + x = 3`.
			First, graph both equations on the same axes. The two lines intersect once. That means there is only one solution to the system.
	The point of intersection appears to be `(1, 2)`.		Read the point from the graph as accurately as possible.
	`y - x = 1` `2 - 1 = 1` `1 = 1` TRUE `(1, 2)` is a solution of `y - x = 1`.	`y + x = 3` `2 + 1 = 3` `3 = 3` TRUE `(1, 2)` is a solution of `y + x = 3`.	Check the values in both equations. Substitute `1` for `x` and `2` for `y`. `(1, 2)` is a solution.
Answer	`(1, 2)` is the solution to the system `y - x = 1` and `y + x = 3y + x = 3`.		Since `(1, 2)` is a solution for each of the equations in the system, it is the solution for the system.

Example
Problem	How many solutions does the system `y = 2x + 1` and `-4x + 2y = 2` have?
		First, graph both equations on the same axes. The two equations graph as the same line. So every point on that line is a solution for the system of equations.
Answer	The system `y = 2x + 1` and `-4x + 2y = 2` has an infinite number of solutions.

Which point is the solution to the system `x - y = -1` and `2x - y = -4`? The system is graphed correctly below.

A coordinate plane shows two lines with positive slopes. One line crosses the x-axis at (negative 2, zero) and the y-axis at (zero, 4), and is labeled 2 x minus y equals negative 4. The second line crosses the x-axis at (negative 1, 0) and the y-axis at (0, 1), and is labeled x minus y equals negative 1. The lines intersect at (negative 3, negative 2).

A) `(-1, 2)`

B) `(-4, -3)`

C) `(-3, -2)`

D) `(-1, 1)`

Show/Hide Answer

Graphing for a Real-World Context

Graphing a system of equations for a real-world context can be valuable in visualizing the problem. Let’s look at a couple of examples.

Example
Problem	In yesterday’s basketball game, Cheryl scored `17` points with a combination of `2`-point and `3`-point baskets. The number of `2`-point shots she made was one greater than the number of `3`-point shots she made. How many of each type of basket did she score?
	`x =` the number of `2`-point shots made `y =` the number of `3`-point shots made		Assign variables to the two unknowns -- the number of each type of shots.
	`2x =` the points from `2`-point baskets `3y =` the points from `3`-point baskets		Calculate how many points are made from each of the two types of shots.
	The number of points Cheryl scored `(17)=` the points from `2`-point baskets `+` the points from `3`-point baskets. `17 = 2x + 3y`		Write an equation using information given in the problem.
	The number of `2`-point baskets `(x) = 1 +` the number of `3`-point baskets `(y)`		Write a second equation using additional information given in the problem.
	`x = 1 + y` `17 = 2x + 3y` `x = 1 + y`		Now you have a system of two equations with two variables.
			Graph both equations on the same axes. The two lines intersect, so they have only one point in common. That means there is only one solution to the system.
	The point of intersection appears to be `(4, 3)`.		Read the point of intersection from the graph.
	`17 = 2x+3y` `17 = 2(4) + 3(3)` `17 = 8 + 9` `17 = 17` TRUE `(4, 3)` is a solution of `17 = 2x + 3y`.	`x = 1 + y` `4 = 1 + 3` `4 = 4` TRUE `(4, 3)` is a solution of `x = 1 + y`	Check `(4, 3)` in each equation to see if it is a solution to the system of equations. `(4, 3)` is a solution to the equation. `x = 4` and `y = 3`
Answer	Cheryl made `4` two-point baskets and `3` three-point baskets.

Example
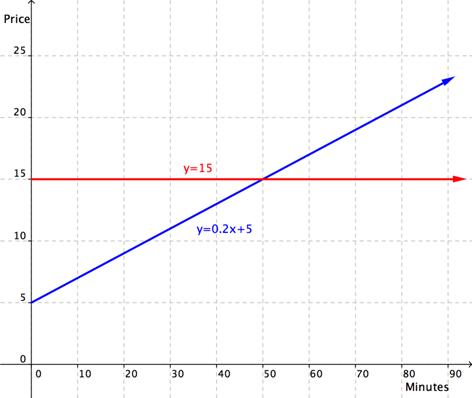
Problem	Andres was trying to decide which of two mobile phone plans he should buy. One plan, TalkALot, charged a flat fee of `$15` per month for unlimited minutes. Another plan, FriendFone, charged a monthly fee of `$5` in addition to charging `20`¢ per minute for calls. To examine the difference in plans, he made a graph: If he plans to talk on the phone for about `70` minutes per month, which plan should he purchase?
		Look at the graph. TalkALot is represented as `y = 15`, while FriendFone is represented as `y = 0.2x + 5`. The number of minutes is listed on the `x`-axis. When `x = 70`, TalkALot costs `$15`, while FriendFone costs about `$19`.
Answer	Andres should buy the TalkALot plan.	Since TalkALot costs less at `70` minutes, Andres should buy that plan.

Note that if the estimate for FriendFone had been incorrect, a new estimate could have been made. Regraphing to zoom in on the area where the lines cross would help make a better estimate.

Paco and Lisel spent `$30` going to the movies last night. Paco spent `$8` more than Lisel.

If `P = "the"` amount that Paco spent, and `L = "the"` amount that Lisel spent, which system of equations can you use to figure out how much each of them spent?

`P + L = 30`

`P + 8 = L`

`P + L = 30`

`P = L + 8`

`P + 30 = L`

`P - 8 = L`

`L + 30 = P`

`L - 8 = P`

Show/Hide Answer

Summary

A system of linear equations is two or more linear equations that have the same variables. You can graph the equations as a system to find out whether the system has no solutions (represented by parallel lines), one solution (represented by intersecting lines), or an infinite number of solutions (represented by two superimposed lines). While graphing systems of equations is a useful technique, relying on graphs to identify a specific point of intersection is not always an accurate way to find a precise solution for a system of equations.