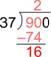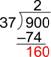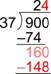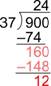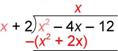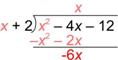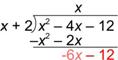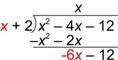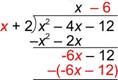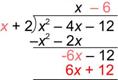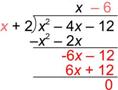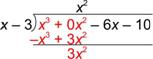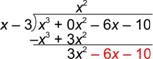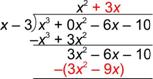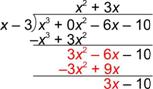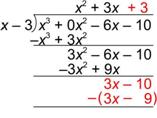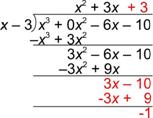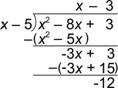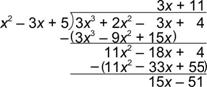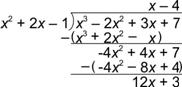Dividiendo Entre Binomios y Polinomios
Objetivos de Aprendizaje
· Dividir un polinomio entre un binomio.
· Dividir un polinomio entre otro polinomio.
Introducción
La división de un polinomio entre un monomio puede manejarse dividiendo separadamente cada término en el polinomio. Esto no se puede hacer cuando el divisor tiene más de un término. Sin embargo, el proceso de división larga puede ser muy útil con los polinomios.
Primero, recuerda cómo puedes usar la división larga para dividir números enteros, por ejemplo 900 entre 37.
|
| Primero, pensarías en cuántos 37s hay en 90, porque 9 es muy pequeño. (Nota: también podrías pensar, cuántos 40s hay en 90.) |
|
| Hay dos 37s en 90, entonces escribes 2 sobre el último dígito de 90. Dos 37s es 74; escribe ese producto debajo del 90. |
|
| Resta: 90 – 74 es 16. (Si el resultado es mayor que el divisor, 37, entonces necesitas usar un número mayor para el cociente.) |
|
| Baja el siguiente dígito (0) y considera cuántos 37 hay en 160. |
|
| Hay cuatro 37s en 160, entonces escribe 4 a un lado del 2 en el cociente. Cuatro 37s es 148; escribe ese producto debajo del 160. |
|
| Resta: 160 – 148 es 12. Esto es menos que 37 por lo que 4 es correcto. Como ya no hay más dígitos en el dividendo para bajar, ya terminaste. |
La respuesta final es 24 R12, o 
. Puedes comprobar esto multiplicando el cociente (sin el residuo) por el divisor, y luego sumar el residuo. El resultado debe ser el dividendo:
24 • 37 + 12 = 888 + 12 = 900
Para dividir polinomios, usa el mismo proceso. Este ejemplo muestra cómo hacer esto cuando divides entre un binomio.
| Ejemplo | |||
| Problema | Dividir: (x2 – 4x – 12) ¸ (x + 2) | ||
|
|
|
| ¿Cuántas x’s hay en x2? Esto es, ¿cuánto es |
|
|
|
|
Escribe el producto del divisor y la parte del cociente que acabas de encontrar debajo del dividendo. Como x(x + 2) = x2 + 2x, escribe esto debajo, y prepárate para restar.
|
|
|
|
| Reescribe –(x2 + 2x) como su opuesto –x2 – 2x para que puedas sumar el opuesto. (Sumar el opuesto es lo mismo que restar, y es más fácil de hacer.) |
|
|
|
|
Suma -x2 a x2, y -2x a -4x. |
|
|
|
| Baja el -12. |
|
|
|
| Repite el proceso. ¿Cuántas veces cabe x en -6x? En otras palabras, ¿cuánto es |
|
|
|
| Como |
|
|
|
| Reescribe –(-6x – 12) como 6x + 12, para que puedas sumar el opuesto. |
|
|
|
| Suma. En este caso, no hay residuo, por lo que ya terminaste. |
| Respuesta | (x2 – 4x – 12) ¸ (x + 2) = x – 6 |
|
|
?
Comprueba esto multiplicando:
(x – 6)(x + 2) = x2 + 2x – 6x – 12 = x2 – 4x – 12
Intentemos con otro ejemplo. En este ejemplo, “falta” un término del dividendo
| Ejemplo | |||
| Problema | Dividir: (x3 – 6x – 10) ¸ (x – 3) | ||
|
|
|
| Observa que hay un término x3 pero no hay un término x2. Suma 0x2 para “apartar el lugar” para este término. (Como 0 veces cualquier cosa es 0, no estás cambiando el valor del dividendo.) |
|
|
|
| Observa los primeros términos: ¿cuántas x’s hay en x3? Como
Multiplica x2(x – 3) = x3 – 3x2, escribe esto debajo del dividendo y prepárate para restar. |
|
|
|
| Reescribe la resta usando el opuesto de la expresión x3 – 3x2. Luego suma. |
|
|
|
| Baja el resto de la expresión en el dividendo Es útil bajar todos los términos restantes. |
|
|
|
| Ahora, repite el proceso con el resto de la expresión, 3x2 – 6x – 10, como el dividendo. |
|
|
|
| ¡Recuerda cuidarlos signos! |
|
|
|
| ¿Cuántas x’s hay en 3x? Como hay 3, multiplica 3(x – 3) = 3x – 9, escribe esto debajo del dividendo y prepárate para restar. |
|
|
|
| Continúa hasta que el grado del residuo sea menor que el grado del divisor. En este caso el grado del residuo, -1, es 0, que es menor que el grado de x – 3, que es 1.
También observa que has bajado todos los términos en el dividendo, y que el cociente se extiende al extremo derecho del dividendo. Estas son otras formas de revisar si ya completaste el problema. |
| Respuesta | (x3 – 6x – 10) ¸ (x – 3) = x2 + 3x + 3 R -1, x2 + 3x + 3 + x2 + 3x + 3 – |
| Puedes reescribir el residuo usando el símbolo R, o como una fracción sumada al resto del cociente con el residuo en el numerador y el divisor en el denominador. En este caso, como el residuo es negativo, puedes restar el opuesto. |
= x2, pon x2 en el cociente.
, o
Comprueba el resultado:
| (x – 3)(x2 + 3x + 3) | = | x(x2 + 3x + 3) – 3(x2 + 3x + 3) |
|
| = | x3 + 3x2 + 3x – 3x2 – 9x – 9 |
|
| = | x3 – 6x – 9 |
|
|
|
|
| x3 – 6x – 9 + (-1) | = | x3 – 6x – 10 |
| Dividir: (x2 – 8x + 3) ¸ (x – 5)
A) x – 3 –
B) x – 13 +
C) x – 13 –
D) x – 15
|
El proceso anterior funciona para dividir cualquier polinomio, no importa cuántos términos hay en el divisor o en el dividendo. Lo importante a recordar es:
· Cuando restes, asegúrate de restar toda la expresión, no sólo el primer término. ¡Esto es muy fácil de olvidar, así que ten cuidado!
· Detente cuando el grado del residuo es menor que el grado del dividendo, o cuando hayas bajado todos los términos en el dividendo, y que el cociente se extiende al extremo derecho del dividendo.
| Ejemplo | |||
| Problema | Dividir: (3x3 + 2x2 – 3x + 4) ¸ (x2 – 3x + 5) | ||
|
|
|
| Observa los primeros términos: ¿Cuánto es
El grado del residuo es 1, que es menor que el grado del divisor, 2. Ya puedes detenerte. |
| Respuesta | (3x3 + 2x2 – 3x + 4) ¸ (x2 – 3x + 5) = 3x + 11 R 15x – 51, o 3x + 11 + |
|
|
? Como 
Comprueba:
| (x2 – 3x + 5)(3x + 11) | = | (x2 – 3x + 5)(3x) + (x2 – 3x + 5)(11) |
|
| = | 3x3 – 9x2 + 15x + 11x2 – 33x + 55 |
|
| = | 3x3 + 2x2 – 18x + 55 |
|
|
|
|
| 3x3 + 2x2 – 18x + 55 + (15x – 51) | = | 3x3 + 2x2 – 3x + 4 |
| Dividir: (x3 – 2x2 + 3x + 7) ¸ (x2 + 2x – 1)
A) x +
B) x + 8 +
C) x – 4 +
D) 13x – 1
|
Sumario
Dividir polinomios entre polinomios de más de un término puede hacerse usando un proceso muy parecido a la división larga de números enteros. Debes tener cuidado de restar las expresiones completas, no sólo el primer término. Detente cuando el grado del residuo sea menor que el grado del divisor. El residuo se puede escribir usando la notación R o como una fracción sumada al cociente con el residuo en el numerador y el divisor en el denominador.
