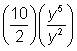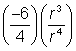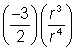Dividiendo Entre un Monomio

 

Objetivos de Aprendizaje

·         Dividir un monomio entre un monomio.

·         Dividir un polinomio entre un monomio.

 

 

La cuarta operación aritmética es la división, el inverso de la multiplicación. La división de polinomios no es tan diferente de la división de números. Empecemos con la división de un monomio entre otro monomio, que es la base de dividir un polinomio entre un monomio.

 

 

Cuando multiplicas dos monomios, multiplicas los coeficientes y luego multiplicas las variables. De manera similar, cuando divides monomios, divides los coeficientes y luego divides las variables. Cuando hay exponentes con la misma base, las reglas de los exponentes dicen que divides restando los exponentes. Considera el siguiente ejemplo:

 

 

 

 

Aquí hay otro ejemplo:

 

 

 

 

Algunas veces la división requiere algo de simplificación.

 

 

 

 

Recuerda que un término no se considera simplificado si contiene un exponente negativo; es por eso que  se reescribió como .

 

 

Divide:   A) 11x4   B) 22x3   C) 11x3   D) 22x4   Mostrar/Ocultar Respuesta A) 11x4 Incorrecto. Dividiste 22 entre 3, pero debes restar los exponentes de la variable x. Como x = x1, esto es x4 – 1 = x3. La respuesta correcta es 11x3.   B) 22x3 Incorrecto. Dividiste las variables correctamente, pero también debes dividir 22 entre 2. La respuesta correcta es 11x3.   C) 11x3 Correcto.  = 11 y x4 – 1 = x3 por lo que la respuesta correcta es 11x3.   D) 22x4 Incorrecto. Divide los coeficientes para obtener  = 11 para el coeficiente. Divide las variables restando los exponentes. Como x = x1, esto es x4 – 1 = x3. La respuesta correcta es 11x3.

 

 

 

La propiedad distributiva dice que puedes distribuir un factor que está siendo multiplicado por una suma o resta, y de la misma manera, puedes distribuir un divisor que está dividido entre una suma o resta (porque una división puede cambiarse a multiplicación.)

 

 

O puedes distribuir el 2, y dividir cada término entre 2.

 

 

Intentemos algo similar con un polinomio.

 

 

 

 

Intentemos con otro ejemplo, observa los signos.

 

 

 

 

Divide:   A)   B)   C)   D)     Mostrar/Ocultar Respuesta A) Correcto. Divide cada término en el polinomio entre el monomio: , lo que da .   B) Incorrecto. Sólo dividiste el primer término. Divide cada término en el polinomio entre el monomio: . La respuesta correcta es .     C) Incorrecto. Eliminaste los dos términos t2, pero no dividiste. Divide cada término en el polinomio entre el monomio: . La respuesta correcta es .   D) Incorrecto. Divide cada término en el polinomio entre el monomio: La respuesta correcta es .

 

 

 

Para dividir un monomio entre un monomio, divide los coeficientes (o simplifícalos como lo harías con una fracción) y divide las variables con bases iguales restando sus exponentes. Para dividir un polinomio entre un monomio, divide cada término del polinomio entre el monomio. ¡Asegúrate de cuidar los signos! Las respuestas finales deben escribirse sin exponentes negativos.