Multiplying Special Cases

Learning Objectives

Square a binomial.
Multiply the sum and difference of the same two terms.

Introduction

While the distributive property can be used for all polynomial multiplication, some products with binomials A polynomial with exactly two terms, such as `5y^2 - 4x` and `x^5 + 6`. can be found using short cuts. These methods are sometimes called special products.

Square of a Binomial Sum

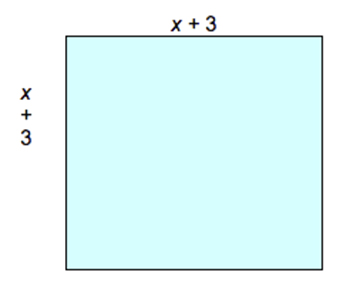
Multiplying a number by itself is often called squaring. You can represent this multiplication as a square. The number being squared is the length of the sides of the square and the product is represented by the area of that square. Consider a square whose side length is described by the binomial `x + 3`:

The image of the square shows the side length is x plus 3.

The area of this square is `(x + 3)(x + 3)` or `(x + 3)^2`.

The following shows the same square, but separates the variable and constant terms:

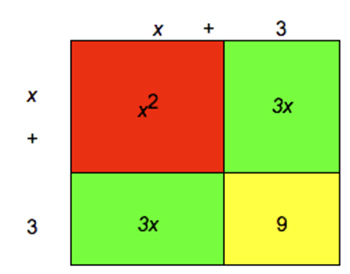
From this area model, you can see that the area can be described by the sum of the red, green and yellow pieces. That is, the area is `x^2 + 3x + 3x + 9 = x^2 + 6x + 9`.

So `(x + 3)^2 = x^2 + 3x + 3x + 9 = x^2 + 6x + 9`.

You can also find the square of a sum of two terms by using the FOIL method.

Example
Problem	Square the binomial. `(x + 5)^2`
	`(x + 5)(x + 5)`	Multiply the binomial by itself.
	First: `xx = x^2` Outer: `x5 = 5x` Inner: `5x = 5x` Last: `55 = 25`
	`x^2 + 5x + 5x + 25`	Add the terms.
	`x^2 + 10x + 25`	Combine like terms.
Answer	`(x + 5)^2 = x^2 + 10x + 25`

Notice that the Outer and Inner terms are the same.

So far, we have two examples of squaring a sum of two terms, one from constructing an area model and one from algebraic calculations:

`(x + 3)^2 = x^2 + 6x + 9`

`(x + 5)^2 = x^2 + 10x + 25`

In both cases, the first term is squared to get the first term of the product. The two terms are multiplied and doubled for the middle term of the product, and the last term is squared for the last term of the product.

This pattern will hold true for the square of the sum of any two terms: Square the first term, add twice the product of the first and the last term, add the last term squared.

Squaring a Binomial Sum

To square a binomial, do the following:

Square the first term.
Add the product of the two middle terms, times two.
Add the square of the last term.

This process is illustrated by the following case: `(a + b)^2 = a^2 + 2ab + b^2`

Example
Problem	Square the binomial. `(2x+6)^2`
	`(2x)^2 = 4x^2`	Square the first term.
	`(2x)(6)(2) = 24x`	Multiply the two terms together and double the product.
	`6^2 = 36`	Square the last term.
	`4x^2 + 24x+36`	Combine the terms.
Answer	`(2x+6)^2 = 4x^2 + 24x+36`

You can check this answer using the distributive property or FOIL.

Find the product:

`(2s + 9)^2`

A) `4s^2 + 81`

B) `4s + 18`

C) `4s^2 + 36s + 81`

D) `4s^2 + 18s + 18`

Show/Hide Answer

Square of a Binomial Difference

Is there also a pattern when you square the difference between two terms? Yes! Since subtraction can be expressed as adding the opposite, a similar pattern does occur.

Consider the square of the binomial `(x - 7)`. You can use FOIL.

Example
Problem	Square the binomial. `(x - 7)^2`
	`(x - 7)(x - 7)`	Rewrite as multiplication.
	First: `xx = x^2` Outer: `x-7 = -7x` Inner: `-7x = -7x` Last: `-7-7 = 49`
	`x^2 + (-7x) + (-7x) + 49`	Add the terms.
	`x^2 - 14x + 49`	Combine the like terms.
Answer	`(x - 7)^2 = x^2 - 14x + 49`

Notice that the pattern is similar to when you square the sum of a binomial.

Squaring a Binomial Difference

To square a binomial difference, do the following:

Square the first term
Subtract the product of the two middle terms, times two
Add the square of the last term.

`(a - b)^2 = a^2 - 2ab + b^2`

Example
Problem	Square the binomial. `(4s - 3)^2`
	`(4s)^2 = 16s^2`	Square the first term, including the coefficient.
	`(4s)(-3)(2) = -24s`	Multiply the two terms together and double the product.
	`(-3)^2 = 9`	Square the last term.
	`16s^2 - 24s + 9`	Add the terms.
Answer	`(4s - 3)^2 = 16s^2 - 24s + 9`

Square the binomial.

`(2r - 9)^2`

A) `4r^2 - 81`

B) `4r - 18`

C) `4r^2 - 36r + 81`

D) `4r^2 + 18r - 18`

Show/Hide Answer

Product of a Sum and a Difference

There is a third special product to consider among binomials: the product of the sum of two terms and the difference of the same two terms. In this case, there is also a pattern. Here is an example:

Example
Problem	Multiply the binomials. `(x + 8)(x - 8)`
	First: `xx = x^2` Outer: `x-8 = -8x` Inner: `8x = +8x` Last: `8-8 = -64`
	`x^2 - 8x + 8x - 64`	Add the terms.
Answer	`(x + 8)(x - 8)=x^2 - 64`

Note that the answer to this binomial product is a binomial itself: the difference of two perfect squares. There is no middle term in this case. Why does this happen? The two terms are opposites and therefore add to zero.

Product of a Sum and a Difference

The product of the sum of two terms `(a + b)` and the difference of the same terms `(a - b)` is the difference of the squares of the two terms.

`(a + b)(a - b) = (a - b)(a + b) = a^2 - b^2`

Example
Problem	Multiply the binomials. `(2n - 5)(2n + 5)`
	`(2n)^2 = 4n^2`	Square the first term, including the coefficient.
	`(5)^2 = 25`	Square the last term.
	`4n^2 - 25`	Take the difference.
Answer	`(2n - 5)(2n + 5) = 4n^2 - 25`

Find the product:

`(2r - 9)(2r + 9)`

A) `4r^2 - 81`

B) `4r - 18`

C) `4r^2 - 36r + 81`

D) `4r^2 - 36r - 81`

Show/Hide Answer

Summary

Some products of multiplying binomials follow a predictable pattern that makes it easy to multiply them. These are known as special products. There are three special products of binomials that each follow a specific formula: squaring the sum of a binomial, squaring the difference of a binomial, and the product of a sum and a difference.