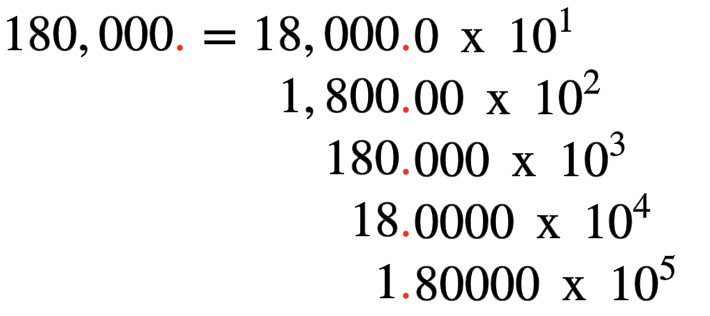
Scientific Notation

Learning Objectives

Convert between scientific and decimal notation.
Multiply and divide using scientific notation.
Solve application problems.

Introduction

When working with very large or very small numbers, scientists, mathematicians, and engineers often use scientific notationA positive number is written in scientific notation if it is written as `a " x " 10^n` where the coefficient `a` has a value such that `1 ≤ a < 10` and `n` is an integer. to express those quantities. Scientific notation uses exponential notation. The following are examples of scientific notation.

Light year: number of miles light travels in one year, about `5,880,000,000,000`

Scientific notation is `5.88" x "10^12` miles.

hydrogen atom: has a diameter of about `0.00000005` millimeters

Scientific notation is `5" x "10^-8` millimeters

Computation with very large numbers is made easier with scientific notation.

Learning to Use Scientific Notation

When a number is written in scientific notation, the exponentWhen a number is expressed in the form `a^b`, `b` is the exponent. The exponent indicates how many times the base is used as a factor. Power and exponent mean the same thing. tells you if the term is a large or a small number. A positive exponent indicates a large number and a negative exponent indicates a small number that is between `0` and `1`.

Since it’s so useful, let’s look more closely at the details of scientific notation format.

Scientific Notation

A positive number is written in scientific notation if it is written as `a" x "10^n` where the coefficient `a` has a value such that `1<=a<10` and `n` is an integer.

Look at the numbers below. Which of the numbers is written in scientific notation?

Number	Scientific Notation?	Explanation
`1.85 text ( x ) 10^-2`	yes	`1<=1.85<10` `-2` is an integer
`1.083text( x ) 10^(1/2)`	no	`1/2` is not an integer
`0.82 text ( x ) 10^14`	no	`0.82` is not `>=1`
`10 text ( x ) 10^3`	no	`10` is not `<10`

Which number below is written in scientific notation?

A) `4.25" x "10^(0.08)`

B) `0.425" x "10^7`

C) `42.5" x "10^5`

D) `4.25" x "10^6`

Show/Hide Answer

Writing Decimal Notation in Scientific Notation

Now let’s compare some numbers expressed in both scientific notation and standard decimal notation in order to understand how to convert from one form to the other. Take a look at the tables below. Pay close attention to the exponent in the scientific notation and the position of the decimal point in the decimal notation.

Large Numbers
Decimal Notation	Scientific Notation
`500.0`	`5" x "10^2`
`80,000.0`	`8" x "10^4`
`43,000,000.0`	`4.3" x "10^7`
`62,500,000,000.0`	`6.25" x "10^10`

Small Numbers
Decimal Notation	Scientific Notation
`0.05`	`5" x "10^-2`
`0.0008`	`8" x "10^-4`
`0.00000043`	`4.3" x "10^-7`
`0.000000000625`	`6.25" x "10^-10`

To write a large number in scientific notation, move the decimal point to the left to obtain a number between `1` and `10`. Since moving the decimal point changes the value, you have to multiply the decimal by a power of `10` so that the expression has the same value.

Let’s look at an example.

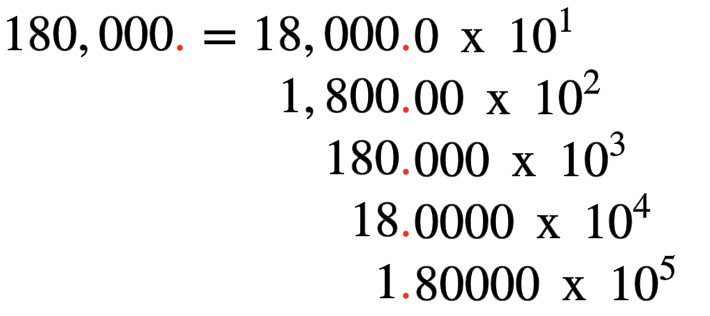
`180,000 = 1.8" x "10^5`

Notice that the decimal point was moved `5` places to the left, and the exponent is `5`.

The world population is estimated to be about `6,800,000,000` people. Which answer expresses this number in scientific notation?

A) `7" x "10^9`

B) `0.68" x "10^10`

C) `6.8" x "10^9`

D) `68" x "10^8`

Show/Hide Answer

Advanced Question

Represent `1.00357" x "10^-6` in decimal form.

A) `1.00357000000`

B) `0.000100357`

C) `0.000001357`

D) `0.00000100357`

Show/Hide Answer

To write a small number (between `0` and `1`) in scientific notation, you move the decimal to the right and the exponent will have to be negative.

`0.00004 = 4" x "10^-5`

You may notice that the decimal point was moved five places to the right until you got the number `4`, which is between `1` and `10`. The exponent is `-5`.

Writing Scientific Notation in Decimal Notation

You can also write scientific notation as decimal notation. For example, the number of miles that light travels in a year is `5.88" x "10^12`, and a hydrogen atom has a diameter of `5" x "10^-8 "mm"`. To write each of these numbers in decimal notation, you move the decimal point the same number of places as the exponent. If the exponent is positive, move the decimal point to the right. If the exponent is negative, move the decimal point to the left.

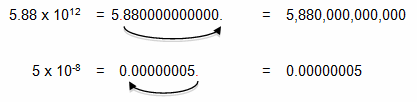
An image shows two equations. In the top equation, the decimal notation of 5.88 times 10 to the twelfth power equals, 5.880000000000 point, equals, 5,880,000,000,000. The decimal point moves right twelve places. In the bottom equation, the decimal notation of 5 times 10 to the negative eighth power equals, 0.00000005, equals 0.00000005. The decimal point moves left 8 places.

For each power of `10`, you move the decimal point one place. Be careful here and don’t get carried away with the zeros; the number of zeros after the decimal point will always be `1` less than the exponent because it takes one power of `10` to shift that first number to the left of the decimal.

Rewrite `1.57" x "10^-10` in decimal notation.

A) `15,700,000,000`

B) `0.000000000157`

C) `0.0000000000157`

D) `157" x "10^-12`

Show/Hide Answer

Multiplying and Dividing Numbers Expressed in Scientific Notation

Numbers that are written in scientific notation can be multiplied and divided rather simply by taking advantage of the properties of numbers and the rules of exponents that you may recall. To multiply numbers in scientific notation, first multiply the numbers that aren’t powers of `10` (the `a` in `a " x "10^n`). Then multiply the powers of ten by adding the exponents.

This will produce a new number times a different power of `10`. All you have to do is check to make sure this new value is in scientific notation. If it isn’t, you convert it.

Let’s look at some examples.

Example
Problem	`(3" x "10^8)(6.8" x "10^-13)`
	`(3" x "6.8)(10^8" x "10^-13)`	Regroup, using the commutative and associative properties.
	`(20.4)(10^8" x "10^-13)`	Multiply the coefficients.
	`20.4" x "10^-5`	Multiply the powers of `10`using the Product Rule: add the exponents.
	`(2.04" x "10^1)" x "10^-5`	Convert `20.4` into scientific notation by moving the decimal point one place to the left and multiplying by `10^1`.
	`2.04" x "(10^1" x "10^-5)`	Group the powers of `10` using the associative property of multiplication.
	`2.04" x "10^(1+(-5))`	Multiply using the Product Rule: add the exponents.
Answer	`(3" x "10^8)(6.8" x "10^-13)=2.04" x "10^-4`

Advanced Example
Problem	`(8.2" x "10^6)(1.5" x "10^-3)(1.9" x "10^-7)`
`(8.2" x "1.5" x "1.9)(10^6" x "10^-3" x "10^-7)`		Regroup, using the commutative and associative properties.
`(23.37)(10^6" x "10^-3" x "10^-7)`		Multiply the numbers.
	`23.37" x "10^-4`	Multiply the powers of `10` using the Product Rule: add the exponents.
	`(2.337" x "10^1)" x "10^-4`	Convert `23.37` into scientific notation by moving the decimal point one place to the left and multiplying by `10^1`.
	`2.337" x "(10^1" x "10^-4)`	Group the powers of `10` using the associative property of multiplication.
	`2.337" x "10^(1+(-4))`	Multiply using the Product Rule and add the exponents.
Answer	`(8.2" x "10^6)(1.5" x "10^-3)(1.9" x "10^-7)=2.337" x "10^-3`

In order to divide numbers in scientific notation, you once again apply the properties of numbers and the rules of exponents. You begin by dividing the numbers that aren’t powers of `10` (the `a` in `a " x "10^n`). Then you divide the powers of `10` by subtracting the exponents.

This will produce a new number times a different power of `10`. If it isn’t already in scientific notation, you convert it, and then you’re done.

Let’s look at some examples.

Example
Problem	`(2.829" x " 10^-9)/(3.45" x "10^-3)`
	`(2.829/3.45)(10^-9/10^-3)`	Regroup, using the associative property.
	`(0.82)((10^-9)/10^-3)`	Divide the coefficients.
	`0.82" x " 10^(-9-(-3))` `0.82" x "10^-6`	Divide the powers of `10` using the Quotient Rule: subtract the exponents.
	`(8.2" x "10^-1)" x "10^-6`	Convert `0.82` into scientific notation by moving the decimal point one place to the right and multiplying by `10^-1`.
	`8.2" x " (10^-1" x "10^-6)`	Group the powers of `10` together using the associative property.
	`8.2" x "10^(-1+(-6))`	Multiply the powers of `10`using the Product Rule: add the exponents.
Answer	`(2.829" x "10^-9)/(3.45" x "10^-3)= 8.2" x "10^-7`

Advanced Example
Problem	`((1.37" x " 10^4)(9.85" x "10^6))/(5.0" x " 10^12)`
`((1.37" x " 9.85)(10^6" x " 10^4))/(5.0" x " 10^12)`		Regroup the terms in the numerator according to the associative and commutative properties.
`(13.4945" x "10^10)/(5.0" x "10^12)`		Multiply.
`(13.4945/5.0)(10^10/10^12)`		Regroup, using the associative property.
`(2.6989)(10^10/10^12)`		Divide the numbers.
`(2.6989)(10^(10-12))` `2.6989" x "10^-2`		Divide the powers of `10` using the Quotient Rule: subtract the exponents.
Answer	`((1.37" x "10^4)(9.85" x "10^6))/(5.0" x " 10^12)=2.6989" x "10^-2`

Notice that when you divide exponential terms, you subtract the exponent in the denominator from the exponent in the numerator.

Evaluate `(4" x "10^-10)(3" x "10^5)` and express the result in scientific notation.

A) `1.2" x "10^-4`

B) `12" x "10^-5`

C) `7" x "10^-5`

D) `1.2" x "10^-50`

Show/Hide Answer

Advanced Question

Evaluate `(3.15" x "10^4)(5.15" x "10^-7)` and express the result as a decimal.

A) `0.0162225`

B) `162225`

C) `0.000162225`

D) `16.2225`

Show/Hide Answer

Summary

Scientific notation was developed to assist mathematicians, scientists, and others when expressing and working with very large and very small numbers. Scientific notation follows a very specific format in which a number is expressed as the product of a number greater than or equal to `1` and less than `10`, and a power of `10`. The format is written `a" x "10^n`, where `1<=a<10` and `n` is an integer.

To multiply or divide numbers in scientific notation, you can use the commutative and associative properties to group the exponential terms together and apply the rules of exponents.