Simplify by Using the Product, Quotient, and Power Rules
Learning Objectives
Exponential notation A shorter way to write repeated multiplication. For example, `2^4` means `2 * 2 * 2 * 2`. Two is used as a factor `4` times. was developed to write repeated multiplication more efficiently. There are times when it is easier to leave the expressions in exponential notation when multiplying or dividing. Let’s look at rules that will allow you to do this.
Recall that exponents are a way of representing repeated multiplication. For example, the notation `5^4` can be expanded and written as `5 * 5 * 5 * 5`, or `625`. And don’t forget, the exponent only applies to the number immediately to its left, unless there are parentheses.
What happens if you multiply two numbers in exponential form with the same base? Consider the expression `(2^3)(2^4)`. Expanding each exponent, this can be rewritten as `(2*2*2)(2*2*2*2)` or `2*2*2*2*2*2*2`. In exponential form, you would write the product as `2^7`. Notice, `7` is the sum of the original two exponents, `3` and `4`.
What about `(x^2)(x^6)`? This can be written as `(x * x)(x * x * x * x * x * x) = x * x * x * x * x * x * x * x` or `x^8`. And, once again, `8` is the sum of the original two exponents.
|
The Product Rule for ExponentsTo multiply two exponential terms with the same base, add their exponents. `(x^a)(x^b) = x^(a+b)`
For any number `x` and any integers `a` and `b`, `(x^a)(x^b)=x^(a+b)`.
|
To multiply exponential terms with the same base, simply add the exponents.
|
Example |
||
|
Problem |
Simplify. `(a^3)(a^7)` |
|
|
|
`(a^3)(a^7)` |
The base of both exponents is `a`, so the product rule applies. |
|
|
`a^(3+7)` |
Add the exponents with a common base. |
|
Answer |
`(a^3)(a^7) = a^10` |
|
When multiplying more complicated terms, multiply the coefficients and then multiply the variables.
|
Example |
||
|
Problem |
Simplify. `5a^4*7a^6` |
|
|
|
`35 * a^4 * a^6` |
Multiply the coefficients. |
|
|
`35 * a^(4+6)` |
The base of both exponents is `a`, so the product rule applies. Add the exponents. |
|
|
`35 * a^10` |
Add the exponents with a common base. |
|
Answer |
`5a^4 * 7a^6=35a^10` |
|
|
Simplify the expression, keeping the answer in exponential notation.
`(4x^5)(2x^8)`
A) `8x^5 * x^8`
B) `6x^13`
C) `8x^13`
D) `8x^40`
|
Let’s simplify `(5^2)^4`. In this case, the base is `5^2` and the exponent is `4`, so you multiply `5^2` four times: `(5^2)^4 = 5^2*5^2*5^2*5^2=5^8` (Using the Product Rule, add the exponents).
`(5^2)^4` is a power of a power. It is the fourth power of `5` to the second power. And we saw above that the answer is `5^8`. Notice that the new exponent is the same as the product of the original exponents: `2*4 = 8`.
So, `(5^2)^4 = 5^(2*4)=5^8` (which equals `390,625`, if you do the multiplication).
Likewise, `(x^4)^3 = x^(4*3)=x^12`.
This leads to another rule for exponents: the Power Rule for ExponentsTo raise a power to a power, multiply the exponents. `(x^a)^b = x^(a*b)` . To simplify a power of a power, you multiply the exponents, keeping the base the same. For example, `(2^3)^5 = 2^15`.
|
The Power Rule for Exponents
For any positive number `x` and integers `a` and `b`: `(x^a)^b=x^(a*b)`.
|
|
Example |
|||
|
Problem |
Simplify. `6(c^4)^2` |
||
|
|
`6(c^4)^2`
|
Since you are raising a power to a power, apply the Power Rule and multiply exponents to simplify. The coefficient remains unchanged because it is outside of the parentheses. |
|
|
Answer |
`6(c^4)^2 = 6c^8` |
|
|
|
Example |
||
|
Problem |
Simplify. `a^2(a^5)^3` |
|
|
|
`a^2a^(5*3)` |
Raise `a^5` to the power of `3` by multiplying the exponents together (the Power Rule). |
|
|
`a^2a^15` `a^(2+15)` |
Since the exponents share the same base, `a`, they can be combined (the Product Rule). |
|
Answer |
`a^2(a^5)^3=a^17` |
|
|
Simplify: `-a(a^2)^4`
A) `-a*a^8`
B) `a^7`
C) `-a^7`
D) `-a^9`
|
Let’s look at dividing terms containing exponential expressions. What happens if you divide two numbers in exponential form with the same base? Consider the following expression.
`4^5/4^2`
You can rewrite the expression as: `(4*4*4*4*4)/(4*4)`. Then you can cancel the common factors of `4` in the numerator and denominator: 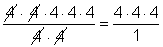
Finally, this expression can be rewritten as `4^3` using exponential notation. Notice that the exponent, `3`, is the difference between the two exponents in the original expression, `5` and `2`.
So, `4^5/4^2=4^(5-2)=4^3`.
Be careful that you subtract the exponent in the denominator from the exponent in the numerator.
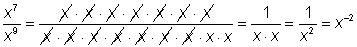
or
`x^7/x^9=x^(7-9)=x^-2`
So, to divide two exponential terms with the same base, subtract the exponents.
|
The Quotient Rule for Exponents For any non-zero number `x` and any integers `a` and `b`: `x^a/x^b=x^(a-b)` For any non-zero number `x` and any integers `a` and `b`: `x^a/x^b=x^(a-b)` |
Notice that `4^2/4^2=4^0`. And we know that `4^2/4^2=16/16=1`. So this may help to explain why `4^0 = 1`.
|
Example |
||
|
Problem |
Evaluate. `4^9/4^4` |
|
|
|
`4^(9-4)`
|
These two exponents have the same base, `4`. According to the Quotient Rule, you can subtract the power in the denominator from the power in the numerator. |
|
Answer |
`4^9/4^4=4^5` |
|
When dividing terms that also contain coefficients, divide the coefficients and then divide variable powers with the same base by subtracting the exponents.
|
Example |
||
|
Problem |
Simplify. `(12x^4)/(2x)` |
|
|
|
`(12/2)(x^4/x)` |
Separate into numerical and variable factors. |
|
|
`6*x^(4-1)` |
Since the bases of the exponents are the same, you can apply the Quotient Rule. Divide the coefficients and subtract the exponents of matching variables. |
|
Answer |
`(12x^4)/2^x=6x^3` |
|
All of these rules of exponents, the Product Rule, the Power Rule, and the Quotient Rule, are helpful when evaluating expressions with common bases.
|
Example |
||
|
Problem |
Evaluate `(24x^8)/(2x^5)` when `x = 4`. |
|
|
|
`(24/2)(x^8/x^5)` |
Separate into numerical and variable factors. |
|
|
`12*x^(8-5)` |
Divide coefficients, and subtract the exponents of the variables. |
|
|
`12x^3` |
Simplify. |
|
|
`(12)(4^3)=12*64` |
Substitute the value `4` for the variable `x`. |
|
Answer |
`(24x^8)/(2x^5)=768` |
|
Usually, it is easier to simplify the expression before substituting any values for your variables, but you will get the same answer either way.
|
Example |
||
|
Problem |
Simplify. `(a^2(a^5)^3)/(8a^8)` |
|
|
|
`(a^2*a^(5*3))/(8a^8)` |
Use the order of operations with PEMDAS: E: Evaluate exponents. Use the Power Rule to simplify `(a^5)^3`. |
|
|
`(a^2a^15)/(8a^8)` |
|
|
|
`(a^(2+15))/(8a^8)` |
M: Multiply, using the Product Rule as the bases are the same. |
|
|
`a^17/(8a^8)` |
|
|
|
`a^(17-8)/8` |
D: Divide using the Quotient Rule. |
|
Answer |
`(a^2(a^5)^3)/(8a^8)=a^9/8` |
|
There are rules that help when multiplying and dividing exponential expressions with the same base. To multiply two exponential terms with the same base, add their exponents. To raise a power to a power, multiply the exponents. To divide two exponential terms with the same base, subtract the exponents.