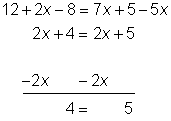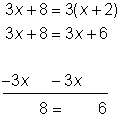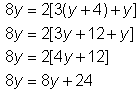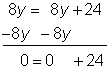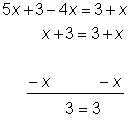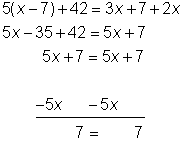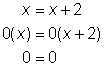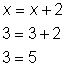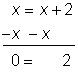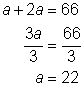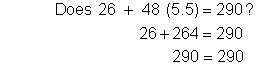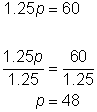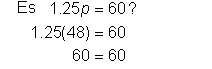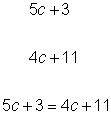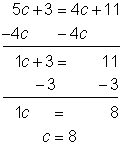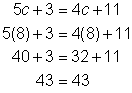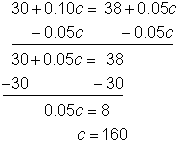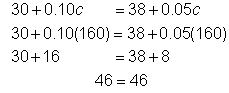Casos Especiales y Aplicaciones

Objetivos de Aprendizaje

· Resolver ecuaciones con una solución, sin solución, o con un número infinito de soluciones.

· Resolver problemas de aplicación usando una ecuación en una variable.

Introducción

Cuando sigues los pasos para resolver una ecuación, intentas despejar la variable. Obtienes una solución cuando tienes la ecuación x = algún valor. Sin embargo, existen ecuaciones que no tienen solución, y otras ecuaciones que tienen un número infinito de soluciones. ¿Cómo sucede esto?

Ecuaciones Algebraicas Sin Solución

Apliquemos los pasos para resolver ecuaciones algebraicas a la ecuación siguiente.

Ejemplo

Problema

Resolver x.

12 + 2x – 8 = 7x + 5 – 5x

Combina los términos semejantes en ambos lados de la ecuación.

Despeja el término x restando 2x de ambos lados.

¡Esta no es la solución! No encontraste el valor de x. Al resolver x de la manera que conoces, llegaste al enunciado inválido 4 = 5. ¡Por supuesto que 4 no es igual a 5!

Esto tiene sentido cuando consideras la segunda línea en la solución donde se combinaron los términos semejantes. Si multiplicas un número por 2 y le sumas 4 nunca obtendrás la misma respuesta porque estarás multiplicando el mismo número por 2 y sumando 5. Como no existe un valor de x que haga este enunciado válido, la respuesta a la ecuación anterior es “no hay solución”.

Ten cuidado de no confundir la solución x = 0 con “no hay solución”. L solución x = 0 significa que el valor 0 satisface la ecuación, entonces sí hay una solución. “No hay solución” significa que no existe ningún valor, ni siquiera 0, que satisface la ecuación.

También debes tener cuidado de no cometer el error de pensar que la ecuación 4 = 5 significa que 4 y 5 son valores de x que son soluciones. Si sustituyes estos valores en la ecuación original, verás que no satisfacen la ecuación. Esto es porque realmente no hay solución — no existen valores de x que hagan que la ecuación 12 + 2x – 8 = 7x + 5 – 5x sea válida.

Ejemplo
Problema	Resolver x. 3x + 8 = 3(x + 2)
		Aplica la propiedad distributiva para simplificar. Despeja el término de la variable. Como sabes que 8 = 6 es falso, no hay solución.
Respuesta	No hay solución.

Ejemplo Avanzado
Problema	Resuelve y. 8y = 2[3(y + 4) + y]
		Aplica la propiedad distributiva para simplificar. Cuando se usan dos juegos de símbolos de agrupación, evalúa el juego de adentro y luego evalúa el de afuera.
		Despeja el término de la variable restando 8y de ambos lados de la ecuación. Como sabes que 0 = 24 es falso, no hay solución.
Respuesta	No hay solución.

Ecuaciones Algebraicas con un Número Infinito de Soluciones

Hemos visto que si una ecuación no tiene solución, te encuentras con un enunciado inválido en lugar de un valor de x. Probablemente se te ocurre que puedes también toparte con un enunciado válido en lugar de un valor de x.

Ejemplo

Problema

Resolver x.

5x + 3 – 4x = 3 + x

Combina términos semejantes a ambos lados de la ecuación.

Despeja el término x restando x de ambos lados.

Llegas al enunciado válido “3 = 3”. Cuando terminas con un enunciado válido como este, significa que la solución a la ecuación es “todos los números reales”. Intenta sustituir x = 0 en la ecuación original — ¡obtendrás un enunciado válido! ¡Intenta con , y también funcionará!

Resulta que esta ecuación tiene un número infinito de soluciones. Cualquier valor de x que se te ocurra funcionará en la ecuación. Cuando piensas en el contexto del problema, esto tiene sentido — la ecuación x + 3 = 3 + x significa que “algún número sumado con 3 es igual al mismo número sumado con 3.” Sabemos que esto siempre es cierto — ¡es la propiedad conmutativa de la suma!

Ejemplo
Problema	Resolver x. 5(x – 7) + 42 = 3x + 7 + 2x
		Aplica la propiedad distributiva y combina los términos comunes para simplificar. Despeja el término x restando 5x de ambos lados. Obtienes el enunciado válido 7 = 7, entonces sabes que x puede ser todos los números reales.
Respuesta	x = todos los números reales

Cuando resuelves una ecuación, multiplicar ambos lados por cero no es una buena idea. Multiplicar ambos lados de una ecuación por 0 siempre resultará en la ecuación 0 = 0, pero la ecuación 0 = 0 no nos ayuda a encontrar la solución de la ecuación original.

Ejemplo
Problema	Resolver x. x = x + 2
		Multiplica ambos lados por cero. Si bien es cierto que 0 = 0, y tengas la tentación de concluir que x es válida para todos los números reales, este no es el caso.
*Comprobar:* *Mejor método:*		Por ejemplo, comprueba y ve si x = 3 resuelve la ecuación. Claramente 3 nunca es igual a 5, entonces x = 3 no es una solución. La ecuación no tiene soluciones.. No fue útil multiplicar ambos lados de la ecuación por cero. Hubiera sido mejor empezar restando x de ambos lados, resultando in 0 = 2, que es enunciado inválido que nos dice que no hay soluciones.
Respuesta	No hay solución.

Al resolver la ecuación algebraica 2(x – 5) = 2x + 10, llegas al resultado −10 = 10. ¿Qué significa esto?

A) x = −10 y 10

B) No existe solución para la ecuación.

C) Debiste cometer un error al resolver la ecuación.

D) x = todos los números reales

Mostrar/Ocultar Respuesta

Pregunta Avanzada

¿Cuántas soluciones tiene la ecuación?:

A) Hay una solución.

B) Hay dos soluciones.

C) Hay un número infinito de soluciones.

D) No hay soluciones.

Mostrar/Ocultar Respuesta

Problemas de Aplicación

El poder del álgebra consiste en cómo te puede ayudar para modelar situaciones reales para resolver preguntas sobre ellos. Esto requiere que seas capaz de traducir problemas del mundo real al lenguaje del álgebra, y luego ser capaz de interpretar correctamente los resultados. Empecemos explorando un problema simple que necesita del álgebra para solucionarse.

El papá de Amanda tiene el doble de la edad de Amanda hoy. La suma de sus edades es 66. Usa una ecuación algebraica para encontrar las edades de Amanda y de su papá.

Una manera de resolver este problema es a prueba y error — puedes elegir algunos números para la edad de Amanda, y calcular la edad de su papá (que es el doble que la de Amanda), y luego combinarlas para ver si resuelven la ecuación. Por ejemplo, si Amanda tiene 20, entonces su papá tendría 40 porque él tiene el doble de la edad de su hija, pero las edades combinadas son 60, no 66. ¿Qué si ella tiene 12, o 15, o 20? Como puedes ver, ¡escoger números al azar es una estrategia muy ineficiente!

Puedes representar esta situación de manera algebraica, que es otra manera de resolver el problema.

Ejemplo
Problema	El papá de Amanda tiene el doble de edad que ella. La suma de sus edades es 66. Encuentra las edades de Amanda y de su papá.
		Necesitamos encontrar la edad de Amanda y la de su papá.		¿Qué nos pide el problema?
				Asigna una variable a la cantidad desconocida. La edad de su papá es dos veces la edad de Amanda.
				La edad de Amanda sumada a la edad de su papá es igual a 66.
				Resuelve las ecuaciones para la variable.
				Usa la edad de Amanda para calcular la edad de su papá.
				¿Tienen sentido estas respuestas?
Respuesta			Amanda tiene 22 años, y su papá tiene 44 años.

Intentemos con otro problema. Considera que la renta de una máquina de jardinería incluye un cargo por renta y otro cargo por cada hora. Podrías usar el álgebra para crear una expresión que te ayude a determinar el costo total para una variedad de situaciones. Una ecuación que contenga esta expresión podría ser útil para tratar de no pasarse de cierto presupuesto.

Ejemplo
Problema	Un jardinero quiere rentar una cortadora de árboles troncos para preparar el área de un jardín. La compañía de renta le cobra $26 por la renta mas $48 por cada hora que se renta la máquina. Escribe una expresión para el costo de la renta para cualquier número de horas.
	El problema pide una expresión algebraica para el costo de la renta por cualquier número de horas. Una expresión tendrá términos, uno de los cuales contiene una variable, pero no contiene un signo igual.	¿Qué pide el problema?
	Veamos los valores en el problema: $26 = por la renta $48 = por cada hora Piensa en lo que esto significa, y trata de identificar un patrón. 1 hr de renta: $26 + $48 2 hr de renta: $26 + $48 + $48 3 hr de renta: $26 + $48 + $48 + $48 Nota que el número “+ $48” en el problema es el mismo que el número de horas que la máquina se renta. Como la multiplicación es una suma repetida, también podrías representarlo así: 1 hr de renta: $26 + $48(1) 2 hr de renta: $26 + $48(2) 3 hr de renta: $26 + $48(3)	¿Cuál es la información importante para encontrar la solución?
	Ahora usemos la variable, h, para representar el número de horas que se rentará la máquina. La renta por h horas: 26 + 48h	¿Cuál es la variable? ¿Qué expresión modela la situación? El total de la renta está determinado por la multiplicación del número de horas por $48 y sumando $26.
Respuesta	El costo de la renta por h horas es 26 + 48h.

Usando la información proporcionada en el problema, pudiste crear una expresión general par esta relación. ¡Esto significa que puedes encontrar el costo de la renta para cualquier número de horas!

Usemos esta expresión para resolver otro problema.

Ejemplo
Problema	Un jardinero quiere rentar una cortadora de árboles troncos para preparar el área de un jardín. La compañía de renta le cobra $26 por la renta mas $48 por cada hora que se renta la máquina. ¿Cuál es el número máximo de horas que el jardinero puede rentar la máquina, si no puede gastar más de $290? (La máquina no puede rentarse por fracciones de hora.)
26 + 48h, donde h = el número de horas.		¿Qué expresión modela esta situación?
		Escribe una ecuación para ayudarte a encontrar cuándo el gasto es igual a $290. Resuelve la ecuación.
		Comprueba la solución.
		Interpreta la respuesta.
Respuesta	El jardinero puede rentar la máquina por 5 horas.

Es útil seguir una lista de pasos para organizar y resolver problemas de aplicación.

Resolviendo Problemas de Aplicación

Sigue los siguientes pasos para traducir la situación del problema a ecuaciones algebraicas que puedas resolver.

1. Lee y entiende el problema.

2. Determina las constantes y las variables del problema.

3. Escribe una ecuación que represente el problema.

4. Resuelve la ecuación.

5. Comprueba el resultado.

6. Escribe un enunciado que responda la pregunta del problema.

Intentemos aplicar los pasos de solución de problemas con algunos ejemplos.

Ejemplo
Problema		Gina ha encontrado un buen precio para toallas de papel. Quiere comprar lo más que pueda para su negocio de limpieza. Las toallas de papel cuestan $1.25 por paquete. Si tiene $60 para gastar, ¿cuántas toallas de papel puede comprar? Escribe la ecuación que Gina podría usar para resolver este problema y muestra la solución.
	El problema pregunta cuántas toallas de papel pueden comprar Gina.		¿Qué es lo que pide el problema?
	Las toallas de papel cuestan $1.25 por paquete. Gina tiene $60 para gastar en toallas de papel.		¿Cuáles son las constantes?
	Sea p = el número de paquetes de toallas de papel.		¿Cuál es la variable?
			¿Qué ecuación representa esta situación? Resolver p. Divide ambos lados de la ecuación entre 1.25 60 ÷ 1.25 = 6,000 ÷ 125 5 00 1,000 1,000 0
			Comprueba tu solución. Sustituye 48 por p en la ecuación.
Respuesta		Gina puede comprar 48 paquetes de toallas de papel.

Ejemplo
Problema	Levon y Maria fueron a comprar velas para decorar las mesas de un restaurante. Levon compró 5 paquetes de velas mas 3 velas sueltas. Maria compró 11 velas sueltas y 4 paquetes de velas. Cada paquete de velas contiene el mismo número de velas. Después de la compra, Maria y Levon se dieron cuenta que ambos compraron exactamente el mismo número de velas. ¿Cuántas velas hay en un paquete?
El problema pregunta cuántas velas hay en un paquete.		¿Qué es lo que pide el problema?
Levon compró 5 paquetes y 3 velas sueltas. Maria compró 4 paquetes y 11 velas sueltas.		¿Cuáles son las constantes?
Sea c = el número de velas en cada paquete.		¿Cuál es la variable?
		¿Qué expresión representa el número de velas que compró Levon? ¿Qué expresión representa el número de velas que compró Maria? ¿Qué ecuación representa esta situación?
		Maria y Levon compraron el mismo número de velas.
		Resolver c. Restar 4c de ambos lados. Restar 3 de ambos lados.
		Comprueba tu solución. Sustituye 8 por c en la ecuación original.
Respuesta	Hay 8 velas en un paquete.

Ejemplo Avanzado
Problema	Se recolecta el dinero de dos máquinas expendedoras. Una máquina contiene 30 billetes de dólar y un puño de dimes. La otra máquina contiene 38 billetes de dólar y un puñado de nickels. El número de monedas en ambas máquinas es el mismo, y la cantidad de dinero que se recolecta de las máquinas también es el mismo. ¿Cuántas monedas hay en cada máquina?
	El problema pregunta cuántas monedas hay en cada máquina.	¿Qué es lo que pide el problema?
	Una máquina tiene 30 billetes de dólar y un puñado de dimes. La otra máquina tiene 38 billetes de dólar y un puñado de nickels — el mismo número de monedas que la primera máquina.	¿Cuáles son las constantes?
	Sea c = el número de monedas en cada máquina.	¿Cuál es la variable?
		¿Cuál es la expresión que representa la cantidad de dinero en la primera máquina?
		¿Cuál es la expresión que representa la cantidad de dinero en la segunda máquina?
		¿Qué expresión representa la situación? La cantidad de dinero en ambas máquinas es la misma.
		Resolver c.
		Comprueba tu solución. Sustituye 160 por c en la ecuación original.
Respuesta	Hay 160 monedas en cada máquina.

Pregunta Avanzada

Albert y Bryn están comprando dulces en la tienda de la esquina. Albert compra 5 bolsas y tres pedazos de dulce individuales; Bryn compra 3 bolsas y luego se come 2 pedazos de una de las bolsas. Cada bolsa tiene el mismo número de dulces.

Después de que Bryn se comió los 2 pedazos, ella se quedó con exactamente la mitad de pedazos de dulce que Albert. ¿Cuántos pedazos de dulce hay en cada bolsa?

Elige la ecuación que podría ser usada para resolver el problema, Usa la variable b para representar el número de pedazos de dulce en una bolsa.

Mostrar/Ocultar Respuesta

Sumario

Algunas ecuaciones se consideran casos especiales. Estas son ecuaciones que no tienen solución y aquellas cuya solución es el conjunto de números reales. Cuando sigues los pasos para resolver una ecuación, y obtienes un enunciado inválido en lugar del valor de la variable, no hay solución. Cuando sigues los pasos para resolver una ecuación, y no has multiplicado ambos lados por cero, y obtienes un enunciado válido en lugar del valor de la variable, la solución es todos los números reales. El álgebra es una herramienta poderosa para modelar y resolver problemas del mundo real.