Subtracting Real Numbers
Subtraction and addition are closely related. They are called inverse operationsA mathematical operation that can reverse or “undo” another operation. Addition and subtraction are inverse operations. Multiplication and division are inverse operations. , because one "undoes" the other. So, just as with integers, you can rewrite subtraction as addition to subtract real numbers.
Inverse operations, such as addition and subtraction, are a key idea in algebra. Suppose you have `$10` and you loan a friend `$5`. An hour later, she pays you back the `$5` she borrowed. You are back to having `$10`. You could represent the transaction like this:
`10 - 5 + 5 = 10`.
This works because a number minus itself is `0`.
`3 - 3 = 0text( )63.5 - 63.5 = 0text( )39,283 - 39,283 = 0`
So, adding a number and then subtracting the same number is like adding `0`.
Thinking about this idea in terms of oppositeAn opposite of a number is the number with the opposite sign, but same absolute value. For example, the opposite of `72` is `-72`. A number plus its opposite is always `0`. numbers, you can also say that a number plus its opposite is also `0`. Notice that each example below consists of a positive and a negative number pair added together.
`3 + (-3) = 0text( )-63.5 + 63.5 = 0text( )39,283 + (-39,283) = 0`
Two numbers are additive inversesAny two numbers whose sum is zero, such as `3` and `-3`, because `3 + (-3) = 0`. if their sum is `0`. Since this means the numbers are opposites (same absolute value but different signs), "additive inverse" is another, more formal term for the opposite of a number. (Note that `0` is its own additive inverse.)
You can use the additive inverses or opposites to rewrite subtraction as addition. If you are adding two numbers with different signs, you find the difference between their absolute values and keep the sign of the number with the greater absolute value.
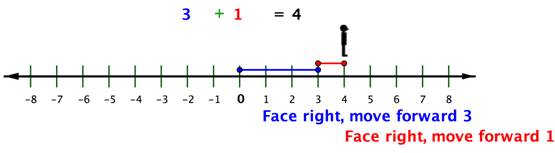
When the greater number is positive, it's easy to see the connection.
`13 + (-7) = 13 - 7`
Both equal `6`.
Let’s see how this works. When you add positive numbers, you are moving forward, facing in a positive direction.

When you subtract positive numbers, you can imagine moving backward, but still facing in a positive direction.
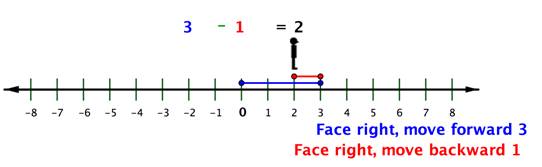
Now let's see what this means when one or more of the numbers is negative.
Recall that when you add a negative number, you move forward, but face in a negative direction (to the left).

How do you subtract a negative number? First face and move forward in a negative direction to the first number, `-2`. Then continue facing in a negative direction (to the left), but move backward to subtract `-3`.

But isn’t this the same result as if you had added positive `3` to `-2`? `-2 + 3 = 1`.
Use the interactive number line below to find the answers to the following pairs of sums and differences, and compare the answers. You will have to specify both numbers and whether you are adding or subtracting.
`3 - 4` and `3 + (-4)`
`2 - (-3)` and `2 + 3`
`-1 - 5` and `-1 + (-5)`
`-2 - (-1)` and `-2 + 1`
In each addition problem, you move in one direction some distance forward. In the paired subtraction problem, you move in the opposite direction the same distance backward. Notice how each gives you the same result!
|
To subtract a real number, you can rewrite the problem as adding the opposite (additive inverse). |
Note, that while this always works, whole number subtraction is still the same. You can subtract `38 - 23` just as you have always done. Or, you could also rewrite it as
`38 + (-23)`. Both ways you will get the same answer.
`38 - 23 = 38 + (-23) = 15`.
It’s your choice in these cases.
|
Example |
||
|
Problem |
Find `23 - 73`. |
|
|
|
|
You can't use your usual method of subtraction, because `73` is greater than `23`. |
|
|
`23 + (-73)` |
Rewrite the subtraction as adding the opposite. |
|
|
`|23| = 23text( and ) |-73| = 73` `73 - 23 = 50` |
The addends have different signs, so find the difference of their absolute values. |
|
Answer |
`23 - 73 = -50` |
Since ` |-73|>|23| `, the final answer is negative. |
|
Example |
||
|
Problem |
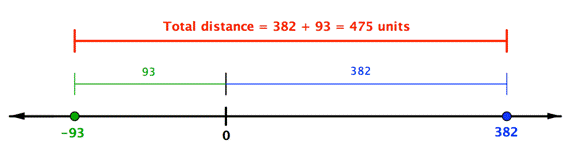
Find `382-(-93)`. |
|
|
|
`382 + 93`
`382 + 93 = 475` |
Rewrite the subtraction as adding the opposite. The opposite of `-93` is `93`. So, this becomes a simple addition problem. |
|
Answer |
`382 - (-93) = 475` |
|
Another way to think about subtracting is to think about the distance between the two numbers on the number line. In the example above, `382` is to the right of `0` by `382` units, and `-93` is to the left of `0` by `93` units. The distance between them is the sum of their distances to `0`: `382 + 93`.
|
Example |
||
|
Problem |
Find `22 1/3-x`, when `x=-3/5.` |
|
|
|
`22 1/3-(-3/5)` |
Substitute `-3/5` for `x` in the expression. |
|
|
`22 1/3+3/5 ` |
Rewrite the subtraction as adding the opposite. The opposite of `-3/5` is `3/5.` |
|
|
`22(1*5)/(3*5)+(3*3)/(5*3)=22 5/15+9/15`
`22 5/15+9/15=22 14/15` |
This is now just adding two rational numbers. Remember to find a common denominator when adding fractions. `3` and `5` have a common multiple of `15`; change denominators of both fractions to `15` (and make the necessary changes in the numerator!) before adding. |
|
Answer |
`22 14/15` |
|
|
Find `-32.3 - (-16.3)`.
A) `-48.6`
B) `-16`
C) `16`
D) `48.6`
|
When you have more than two real numbersAll rational or irrational numbers. to add or subtract, work from left to right as you would when adding more than two whole numbers. Be sure to change subtraction to addition of the opposite when needed.
|
Example |
||
|
Problem |
Find `-23+16-(-32)-4+6`. |
|
|
|
`bb-bb23bb +bb 16 - (-32) - 4 + 6` `bb-bb7 - (-32) - 4 + 6` |
Start with `-23 + 16`. The addends have different signs, so find the difference and use the sign of the addend with the greater absolute value. `-23 + 16 = -7.` |
|
|
`-bb7bb-(bb-bb32)-4+6` `-bb7 bb+ bb32 - 4 + 6` |
Now you have `-7 - (-32)`. Rewrite this subtraction as addition of the opposite. The opposite of `-32` is `32`, so this becomes `-7 + 32`, which equals `25.` |
|
|
`bb25 bb- bb4 + 6` |
You now have `25 - 4`. You could rewrite this as an addition problem, but you don't need to. |
|
`bb21 + 6` |
Complete the final addition of `21 + 6`. |
|
|
Answer |
`-23 + 16 - (-32) - 4 + 6 = 27` |
|
|
Find `32 - (-14) - 2 + (-82)`.
A) `-66`
B) `-38`
C) `98`
D) `126`
|
Situations that use negative numbers can require subtraction as well as addition. As you saw above, sometimes subtracting two positive numbers can give a negative result. You should be sure that a negative number makes sense in the problem.
|
Example |
||
|
Problem
|
Boston is, on average, `7` degrees warmer than Bangor, Maine. The low temperature on one cold winter day in Boston was `3^@text(F)`. About what low temperature would you expect Bangor to have on that day? |
|
|
|
If the temperature in Boston is `x`, the temperature in Bangor is `x - 7`. |
The phrase "`7` degrees warmer" means you can subtract `7` degrees from Boston's temperature to estimate Bangor's temperature. (Note that you can also add `7` degrees to Bangor's temperature to estimate Boston's temperature. Be careful about which should have the greater number!) |
|
|
`x = 3` |
On that day, Boston's low was `3^@.` |
|
Bangor's temperature is `3 - 7` |
Substitute `3` for `x` to get Bangor's temperature. |
|
|
|
`3 - 7 = 3 + (-7)` |
Since `3<7`, rewrite the subtraction problem as addition of the opposite. Add the numbers. Since one is positive and the other is negative, you find the difference of ` |-7|` and ` |3|,` which is `4`. Since ` |-7|>|3|`, the final sum is negative. |
|
Answer |
You would expect the low temperature in Bangor, Maine to be `-4^@text(F)`. |
|
|
Example |
||
|
Problem
|
Everett paid several bills without balancing his checkbook first! When the last check he wrote was still to be deducted from his balance, Everett's account was already overdrawn. The balance was `-$201.35`. The final check was for `$72.66`, and another `$25` will be subtracted as an overdraft charge. What will Everett's account balance be after that last check and the overdraft charge are deducted? |
|
|
|
`-201.35 - 72.66 - 25` |
The new balance will be the existing balance of `-$201.35`, minus the check's amount and the overdraft charge. |
|
|
`-201.35 - 72.66-25` `-201.35+(-72.66)-25` |
Start with the first subtraction, `-201.35 - 72.66`. Rewrite it as the addition of the opposite of `72.66.` |
|
|
`-274.01-25` |
Since the addends have the same signs, the sum is the sum of their absolute values `(201.35 + 72.66)` with the same sign (negative). |
|
`-274.01 + (-25)` |
Again, rewrite the subtraction as the addition of the opposite. |
|
|
|
`-274.01 + (-25) = -299.01` |
Add, by adding the sum of their absolute values and use the same sign as both addends. |
|
Answer |
Everett’s account balance will be `-$299.01`. |
|
|
Example |
||
|
Problem
|
One winter, Phil flew from Syracuse, NY to Orlando, FL. The temperature in Syracuse was `-20^@text(F)`. The temperature in Orlando was `75^@text(F)`. What was the difference in temperatures between Syracuse and Orlando? |
|
|
|
`75 - (-20)` |
To find the difference between the temperatures, you need to subtract. We subtract the ending temperature from the beginning temperature to get the change in temperature. |
|
`75 + 20`
|
Rewrite the subtraction as adding the opposite. The opposite of `-20` is `20`. |
|
|
|
`75 + 20 = 95` |
There is a `95` degree difference between `75^@` and `-20^@`. |
|
Answer |
The difference in temperatures is `95` degrees. |
|
|
Louise noticed that her bank balance was `-$33.72` before her paycheck was deposited. After the check had been deposited, the balance was `$822.98`. No other deductions or deposits were made. How much money was she paid?
|
Subtracting a number is the same as adding its opposite (also called its additive inverse). To subtract, you can rewrite the subtraction as adding the opposite and then use the rules for the addition of real numbers.