Adding Real Numbers
Adding real numbers follows the same rules as adding integers. The number `0` has some special attributes that are very important in algebra. Knowing how to add these numbers can be helpful in real-world situations as well as algebraic situations.
The rules for adding integersThe numbers …, `-3,` `-2,` `-1,` `0,` `1,` `2,` `3`… apply to other real numbers, including rational numbersNumbers that can be written as the ratio of two integers, where the denominator is not zero. .
|
To add two numbers with the same sign (both positive or both negative)
To add two numbers with different signs (one positive and one negative)
|
Remember—to add fractions, you need them to have the same denominator. This is still true when one or more of the fractions are negative.
|
Example |
||
|
Problem |
Find `-3/7+(-6/7)+2/7` |
|
|
|
`|-3/7|=3/7text( and )|-6/7|=6/7`
|
This problem has three addendsA number added to one or more other numbers to form a sum. . Add the first two, and then add the third.
|
|
`3/7+6/7=9/7` |
Since the signs of the first two are the same, find the sum of the absolute values of the fractions. |
|
|
`-3/7+(-6/7)=-9/7` |
Since both addends are negative, the sum is negative. |
|
|
|
`|-9/7|=9/7text( and ) |2/7|=2/7`
`9/7-2/7=7/7` |
Now add the third addend. The signs are different, so find the difference of their absolute values. |
|
|
`-9/7+2/7=-7/7` |
Since `|-9/7|>|2/7|`, the sign of the final sum is the same as the sign of `-9/7`. |
|
Answer |
`-3/7+(-6/7)+2/7=-7/7` |
The answer is `- 7/7`, which can be simplified to `-1`. |
|
Example |
||
|
Problem |
Find `-2 3/4+7/8.` |
|
|
|
`|-2 3/4|=2 3/4text( and )|7/8|=7/8`
`2 3/4-7/8` |
The signs are different, so find the difference of their absolute values. |
|
|
`2 3/4=(2(4)+3)/4=11/4`
|
First rewrite `2 3/4` as an improper fraction, then rewrite the fraction using a common denominator. |
|
`11/4=(11*2)/(4*2)=22/8` |
|
|
|
`22/8-7/8` |
Now substitute the rewritten fraction in the problem. |
|
|
|
`22/8-7/8=15/8` |
Subtract the numerators and keep the same denominator. Simplify to lowest terms, if possible. |
|
Answer |
`-2 3/4+7/8=-15/8` |
Since `|-2 3/4|>|7/8|`, the sign of the final sum is the same as the sign of `-2 3/4`. The answer `- 15/8` can be simplified to `-1 7/8`. |
When you add decimals, remember to line up the decimal points so you are adding tenths to tenths, hundredths to hundredths, and so on.
|
Example |
|
|
Problem |
Find `27.832 + (-3.06)`. |
|
|
Since the addends have different signs, subtract their absolute values. ` |-3.06| = 3.06`
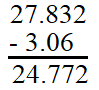
The sum has the same sign as `27.832`, whose absolute value is greater. |
|
Answer |
`27.832 + (-3.06) = 24.772` |
|
Find `-32.22 + 124.3`.
A) `19.79`
B) `44.65`
C) `92.08`
D) `156.52`
|
The rules for adding real numbers refer to the addends being positive or negative. But `0` is neither positive nor negative.
It should be no surprise that you add `0` the way you always have—adding `0` doesn’t change the value.
|
`7 + 0 = 7` |
`-7 + 0 = -7` |
|
`0 + 3.6 = 3.6` |
`-2/23+0=-2/23` |
|
`x + 0 = x` |
`0 + x = x` |
Notice that `x + 0 = x` and `0 + x = x`. This means that it doesn’t matter which addend comes first.
The number `0` is called the additive identityThe number `0` is called the additive identity because when you add it to a number, the result you get is the same number. For example, `4 + 0 = 4`.. The identity property of 0 When you add 0 to any number, the sum is the same as the original number. For example, `55 + 0 = 55`.states that adding `0` to other numbers doesn’t change their value. You can think of it in this way: adding `0` lets the other number keep its identity.
|
What is `0 + y`, when `y = 3`?
A) `-3`
B) `0`
C) `3`
|
There are many situations that use negative numbers. For example, temperatures colder than `0`° are usually described using negative numbers. In golf tournaments, players’ scores are often reported as a number over or under par, instead of the total number of strokes it takes to hit the ball into the hole. (Par is the expected number of strokes needed to complete a hole.) A number under par is negative, and a number over par is positive.
The following examples show how addition of real numbers, including negative numbers, can be useful.
|
Example |
||
|
Problem
|
Boston is, on average, `7` degrees warmer than Bangor, Maine. The low temperature on one cold winter day in Bangor was `-13^@` Fahrenheit. About what low temperature would you expect Boston to have on that day? |
|
|
|
If the temperature in Bangor is `x`, the temperature in Boston is `x + 7`. |
The phrase "`7` degrees warmer" means you add `7` degrees to Bangor's temperature to estimate Boston's temperature. |
|
|
`x = -13` |
On that day, Bangor's low was `-13^@.` |
|
|
Boston's temperature is `-13 + 7`
`-13+7=-6` |
Substitute `-13` for `x` to get Boston's temperature. |
|
Answer |
You would expect Boston to have a temperature of `-6` degrees. |
|
|
Example |
||
|
Problem
|
Before Joanne could deposit her paycheck of `$802.83`, she overdrew her checking account. The balance was `-$201.35`. What was her balance after she deposited the paycheck? |
|
|
|
`-201.35 + 802.83`
|
By depositing her paycheck, Joanne is adding money to her account. The new balance is the sum of the old `(-201.35)` and the paycheck amount. |
|
`-201.35 + 802.83 = 601.83` |
Since the numbers have different signs, find the difference of `-201.35`. Since ` |802.83|>|-201.35|,` the sum is positive. |
|
|
Answer |
The new balance is `$601.48.` |
|
When forces or objects are working in opposite directions, sometimes it's helpful to assign a negative value to one and a positive value to the other. This is done often in physics and engineering, but it could also be done in other contexts, such as football or a tug-of-war.
|
Example |
||
|
Problem
|
Two people are in a tug-of-war contest. They are facing each other, each holding the end of a rope. They both pull on the rope, trying to move the center toward themselves.
Here's an illustration of this situation. The person on the right is pulling in the positive direction, and the person on the left is pulling in the negative direction.
At one point in the competition, the person on the right was pulling with `122.8` pounds of force. The person on the left was pulling with `131.3` pounds of force. The forces on the center of the rope, then, were `122.8` lbs and `-131.3` lbs. a) What was the net (total sum) force on the center of the rope? b) In which direction was it moving? |
|
|
Net force `= 122.8+(-131.3)` |
The net force is the sum of the two forces on the rope. |
|
|
|
|
|
|
|
Net force `= -8.5` |
To find the sum, add the difference of the absolute values of the addends. Since` |-131.3|>122.8 `, the sum is negative. |
|
Answer |
The net force is `-8.5` lbs (or `8.5` lbs to the left). The center of the rope is moving to the left (the negative direction). |
Notice that it makes sense that the rope was moving to the left, since that person was pulling with more force. |
|
After Bangor reached a low temperature of `-13^@,` the temperature rose only `4` degrees higher for the rest of the day. What was the high temperature that day?
A) `-17`
B) `-9`
C) `9`
D) `17`
|
As with integers, adding real numbers is done following two rules. When the signs are the same, you add the absolute values of the addends and use the same sign. When the signs are different, you subtract the absolute values and use the same sign as the addend with the greater absolute value. Adding `0`, which is neither positive nor negative, is done using the additive identity of `0`: `x + 0 = x` and `0 + x = x`, for any value of `x`.
