Adding Integers

Learning Objectives

Introduction

On an extremely cold day, the temperature may be `-10`. If the temperature rises `8` degrees, how will you find the new temperature? Knowing how to add integers is important here and in much of algebra.

Adding Integers with the Same Sign

Since positive integersThe numbers …, `-3,` `-2,` `-1,` `0,` `1,` `2,` `3`… are the same as natural numbers, adding two positive integers is the same as adding two natural numbers. To add positive integers on the number line, you move to the right (in the positive direction).

Supplemental Interactive Activity

Try out the interactive number line below. Choose a few pairs of positive integers to add. Click and drag the blue and red dots, and watch how the addition works.

To add negative integers on a number line, you move to the left (in the negative direction). 

Supplemental Interactive Activity

Try out the interactive number line below. Choose a few pairs of negative integers to add. Click and drag the blue and red dots, and watch how the subtraction works.

In both cases, the total number of units moved is the total distance moved. Since the distance of a number from `0` is the absolute value of that number, then the absolute value of the sum of the integers is the sum of the absolute values of the addendsA number added to one or more other numbers to form a sum. .

When both numbers are negative, you move left in a negative direction, and the sum is negative. When both numbers are positive, you move right in a positive direction, and the sum is positive.

To add two numbers with the same sign (both positive or both negative):

 

  • Add their absolute values and give the sum the same sign.

 

Example

Problem

Find `-23+(-16)`.

 

 

Both addends have the same sign (negative).

 

So, add their absolute values:` |-23| = 23" and" |-16| = 16`

 

The sum of those numbers is `23 + 16 = 39`.

 

 

Since both addends are negative, the sum is negative.

Answer

`-23 + (-16) = -39`

With more than two addends that have the same sign, use the same process with all addends.

Example

Problem

Find `-27+(-138)+(-55).`

 

 

All addends have the same sign (negative).

 

So, add their absolute values:

` |-27| = 27, |-138|=138,` and `|-55|=55`

 

The sum of those numbers is `27 + 138 + 55 = 220.`

 

Since all addends are negative, the sum is negative.

Answer

`-27 + (-138) + (-55) = -220`

 

Find `-32 + (-14)`.

 

A) `46`

 

B) `18`

 

C) `-18`

 

D) `-46`

 

+ 

Show/Hide Answer

 

Adding Integers with Different Signs

What happens when the addends have different signs, like in the temperature problem in the introduction? If it’s `-10` degrees, and then the temperature rises `8` degrees, the new temperature is `-10 + 8`. How can you calculate the new temperature?

When you add a positive integer and a negative integer, you move in the positive (right) direction to the first number, and then move in the negative (left) direction to add the negative integer.

Since the distances overlap, the absolute value of the sum is the difference of their distances. So to add a positive number and a negative number, you subtract their absolute values (their distances from `0`).

Supplemental Interactive Activity

Try adding integers with different signs with this interactive number line. Move in a positive direction (right) to add a positive number, and move in a negative direction (left) to add a negative number. See if you can find a rule for adding numbers without using the number line.

What is the sign of the sum of a positive and a negative integer? It’s pretty easy to figure out. If you moved further to the right than you did to the left, you ended to the right of `0`, and the answer is positive; and if you move further to the left, the answer is negative.

A number line goes from negative 8 to positive 8 with 15 labeled marks in between, and each mark increases by 1. Above the number line is the equation negative 1 plus 4 equals 3. Parallel to the number line, a line starts at 0 and moves left 1 space, ending on a point at negative 1. A label reads, “Face left, move forward negative 1.” Another line above that starts with a point at negative 1 and moves right 4 spaces, ending on a point at positive 3. A label reads, “Face right, move forward 4.” A silhouette of a person is shown directly above positive 3. The implication is that the person started at zero, took one step in the negative direction, then took four steps in the positive direction to end at positive 3.

If you didn’t have the number line to refer to, you could find the sum of `-1 + 4` by

Look at the illustration below.

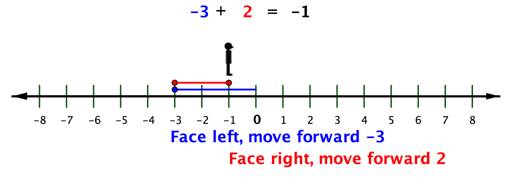
A number line goes from negative 8 to positive 8 with 15 labeled marks in between, and each mark increases by 1. Above the number line is the equation negative 3 plus 2 equals negative 1. Parallel to the number line, a line starts at 0 and left 3 spaces, ending on a point at negative 3. A label reads, “Face left, move forward negative 3.” Another line above that starts with a point at negative 3 and moves right 2 spaces, ending on a point at negative 1. A label reads, “Face right, move forward 2.” A silhouette of a person is shown directly above negative 1. The implication is that the person started at zero, took three steps in the negative direction, then took two steps in the positive direction to end at negative 1

If you didn’t have the number line to refer to, you can find the sum of `-3 + 2` by

To add two numbers with different signs (one positive and one negative):

 

  • Find the difference of their absolute values.
  • Give the sum the same sign as the number with the greater absolute value.

Note that when you find the difference of the absolute values, you always subtract the lesser absolute value from the greater one. The example below shows you how to solve the temperature question that you considered earlier.

Example

Problem

Find `8 + (-10)`.

 

 

The addends have different signs.

So find the difference of their absolute values.

 

`|-10| = 10text( and ) |8| = 8`

 

The difference of the absolute values is `10 - 8 = 2`.

 

Since `10` > `8`, the sum has the same sign as `-10`.

Answer

`8 + (-10) = -2`

 

Example

Problem

Evaluate `x + 37` when `x = -22`.

 

`x + 37`

`-22 + 37`

Substitute `-22` for `x` in the expression.

 

`|-22| = 22text( and ) |37| = 37`

`37 - 22 = 15`

 

 

 

The addends have different signs. So find the difference of their absolute values.

 

Since ` |37|>|-22|`, the sum has the same sign as `37`.

Answer

`-22 + 37 = 15`

 

With more than two addends, you can add the first two, then the next one, and so on.

Example

Problem

Find `-27 + (-138) + 55`.

 

 

Add two at a time, starting with `-27 + (-138)`.

 

 

Since they have the same signs, you add their absolute values and use the same sign to get `-165`.

 

Now add `-165 + 55`. Since `-165` and `55` have different signs, you add them by subtracting their absolute values. 

 

 

Since `165>55,` the sign of the final sum is the same as the sign of  `-165`.

Answer

`-27 + (-138) + 55 = -110`

 

 

Find `32 + (-14)`.

 

A) `46`

 

B) `18`

 

C) `-18`

 

D) `-46`

 

+ 

Show/Hide Answer

 

Summary

There are two cases to consider when adding integers. When the signs are the same, you add the absolute values of the addends and use the same sign. When the signs are different, you find the difference of the absolute values and use the same sign as the addend with the greater absolute value.