Integers

Learning Objectives

Introduction

You've worked with numbers on a number line. You know how to graph numbers like `0`, `1`, `2`, `3`, etc. on the number line. There are other kinds of numbers that can be graphed on the number line, too. Let's see what they look like and where they are located on the number line.

Natural Numbers and Whole Numbers

In mathematics, it's sometimes helpful to talk about groups of things, which are called setsA collection or group of things such as numbers.. Numbers can be grouped into sets, and a particular number can belong to more than one set.

You probably are familiar with the set of natural numbersAlso called counting numbers, the numbers `1`, `2`, `3`, `4`, … , which are also called the counting numbersAlso called natural numbers, the numbers `1`, `2`, `3`, `4`, .... These are the numbers `1`, `2`, `3`, and so on—the numbers we use when counting.

The following illustration shows the natural numbers graphed on a number line.

A number line goes from 0 to 6 with 5 marks in between. Each mark increases by one. The marks are labeled from 0 to 6. There is a solid point shown on each natural number from 1 to 6.

The number line continues in both directions. The set of natural numbers only continues to the right, so you can include `6`, `7`, and so on, all the way up into the hundreds, thousands, and beyond. You can only show so much on one picture!

When `0` is added to the set of `1`, `2`, `3`, and so on, it forms the set of whole numbersThe numbers `0`, `1`, `2`, `3`, …., or all natural numbers plus `0`.. These are called “whole” because they have no fractional parts. (A trick to help you remember which are natural numbers and which are whole numbers is to think of a “hole,” which can be represented by `0`. The whole ("hole") numbers include `0`, the natural numbers do not.)

The following illustration shows the whole numbers graphed on the number line.

A number line goes from 0 to 6 with 5 marks in between. Each mark increases by one. The marks are labeled from 0 to 6, and there is a solid point shown on each mark.

Integers

When you work with something like temperature, you sometimes want to use numbers that are less than zero, which are called negative numbersNumbers less than `0`.. Negative numbers are written using a negative sign in front, such as `-1`, `-5`, and `-30`. These are read negative one, negative five, and negative thirty. (The negative sign should not be read as minus; minus means subtraction.)

The numbers greater than `0` are called positive numbersNumbers greater than `0`. and can be written with or without the “+” sign. Notice that `0` is neither positive nor negative!

IntegersThe numbers …, `-3,` `-2,` `-1,` `0,` `1,` `2,` `3`… are the numbers: …, `-3`, `-2`, `-1`, `0`, `1`, `2`, `3`, …. Notice that all of the whole numbers are also integers. The following illustration shows the integers graphed on the number line. The integers include zero and continue to the right and to the left.

A number line goes from negative 6 to positive 6 with 11 marks in between. Each mark increases by one. The marks are labeled from negative 6 to positive 6, and there is a solid point shown on each integer.

The number `0` belongs to which of the following sets of numbers?

 

natural numbers

 

whole numbers

 

integers

 

A) natural numbers only

 

B) whole numbers only

 

C) natural and whole numbers

 

D) integers only

 

E) whole numbers and integers

 

+ 

Show/Hide Answer

 

Absolute Value and the Number Line

The number line below shows all the integers between and including `-5` and `5`. Notice that the positive integers go to the right: `1`, `2`, `3`, and so on. The negative integers go to the left: `-1`, `-2`, `-3`, and so on.

A number line goes from negative 6 to positive 6 with 11 marks in between. Each mark increases by one. The marks are labeled from negative 6 to positive 6, and there is a solid point shown on each mark from negative 5 to positive 5.

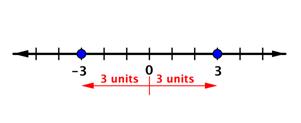
The distance between a number’s place on the number line and `0` is called the number’s absolute valueThe absolute value of a number is its distance from 0 on a number line.. To write the absolute value of a number, use short vertical lines `(|)` on either side of the number. For example, the absolute value of `-3` is written as bar negative three bar.

Notice that distance is always positive or `0`.

`|-3| = 3`, as `-3` is `3` units away from `0` and `|3| = 3`, as `3` is `3` units away from `0`.

A number line goes from negative 3 to 3, with five marks in between. The mark in the center is labeled 0. The mark 3 to the left of 0 is labeled negative 3 and is shown with a point. The mark 3 to the right of 0 is labeled 3 and is shown with a point. Below the number line is a shorter line with a mark in the center, at zero, and arrows on each end. The right-facing arrow starts at 0 and ends at positive 3 and is labeled “3 units.” The left-facing arrow starts and 0 and ends at negative 3, and is also labeled “3 units.”

Here are some other examples.

`|0|=0`
`|-23|=23`
`|6|=6`
`|817|=817`
`|-3,000|=3,000`

 

Example

Problem

Find ` |x| ` when `x=-7`.

 

`|x|`

`|-7|`

Substitute `-7` for `x` in the expression.

 

Answer

`|-7|=7`

Since `-7` is `7` units from `0`, the absolute value is `7.`

To locate an integer on the number line, imagine standing on the number line at `0`. If the number is `0`, you’re there. If the number is positive, face to the right toward numbers greater than `0`. If the number is negative, face to the left toward numbers less than `0`. Then, move forward the number of units equal to the absolute value of the number.

Example

Problem

Find `-4` on the number line. Then determine `|-4|.`

 

A number line has 11 marks. Only the center mark is labeled, showing a 0 and a silhouette of a person directly above it. The person is facing left.

Imagine standing at `0`. Since `-4` is negative, face to the left.

Move `4` units from `0` in the negative direction. 

 

 

 

A number line has 11 marks. The center mark is labeled 0. One mark is labeled negative 4 and has a silhouette of a person directly above it. The person is facing left. Below the number line is a shorter line that begins with a mark at zero and shows an arrow pointing left, ending at negative 4. It is labeled, “4 units.”

Draw a dot on the number line at that location, which is `-4`.

 

Answer

 

`|-4| = 4`

Direction moved does not affect absolute value, only the distance moved.

 

Which point represents `-2` on this number line? 

 

A number line has 11 marks. The center mark is labeled 0. There are five labeled points. Point A is shown on the mark four to the left of 0. Point B is shown on the mark two to the left of 0. Point C is shown on the mark one to the left of 0. Point D is shown on the mark one to the right of 0. Point E is shown on the mark two to the right of 0.

+ 

Show/Hide Answer

 

Opposites

You may have noticed that, except for `0`, the integers come in pairs of positive and negative numbers: `1` and `-1`, `3` and `-3`, `72` and `-72`, and so on. Each number is the oppositeAn opposite of a number is the number with the opposite sign, but same absolute value. For example, the opposite of `72` is `-72`. A number plus its opposite is always `0`. of the other number in the pair: `72` is the opposite of `-72`, and `-72` is the opposite of `72`.

A number and its opposite are the same distance from `0`, so they have the same absolute value.

`|72| = 72`, and `|-72| = 72`

The set of integersThe numbers …,`-3`,`-2`, `-1`, `0`, `1`, `2`, `3`... are all the whole numbers and their opposites.

What is the opposite of `-29`?

 

+ 

Show/Hide Answer

Summary

Some numbers are natural numbers (`1`, `2`, `3`, ...) or whole numbers (`0`, `1`, `2`, `3`, ...). Whole numbers are also integers. There are other integers which are the opposites of the whole numbers (`-1`, `-2,` `-3`, ...). These negative numbers lie to the left of `0` on the number line. Integers are the whole numbers and their opposites. The absolute value of a number is its distance to `0` on the number line. Absolute values are always positive or `0`.