Quadrilaterals

Learning Objective

• Identify properties, including angle measurements, of quadrilaterals.

QuadrilateralsA four-sided polygon. are a special type of polygon. As with triangles and other polygons, quadrilaterals have special properties and can be classified by characteristics of their angles and sides. Understanding the properties of different quadrilaterals can help you in solving problems that involve this type of polygon.

Picking apart the name “quadrilateral” helps you understand what it refers to. The prefix “quad-” means “four,” and “lateral” is derived from the Latin word for “side.” So a quadrilateral is a four-sided polygon.

Since it is a polygonA closed plane figure with three or more straight sides., you know that it is a two-dimensional figure made up of straight sides. A quadrilateral also has four angles formed by its four sides. Below are some examples of quadrilaterals. Notice that each figure has four straight sides and four angles.

The sum of the interior angles of any quadrilateral is `360^@`. Consider the two examples below.

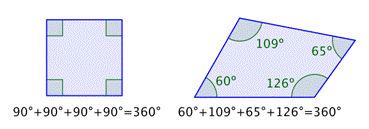
You could draw many quadrilaterals such as these and carefully measure the four angles. You would find that for every quadrilateral, the sum of the interior angles will always be `360^@`.

You can also use your knowledge of triangles as a way to understand why the sum of the interior angles of any quadrilateral is `360^@`. Any quadrilateral can be divided into two triangles as shown in the images below.

In the first image, the quadrilaterals have each been divided into two triangles. The angle measurements of one triangle are shown for each.

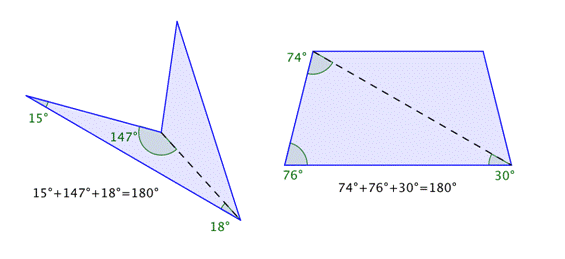
These measurements add up to `180^@`. Now look at the measurements for the other triangles. They also add up to `180^@`!

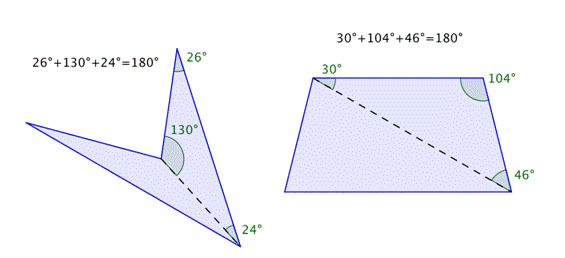
Since the sum of the interior angles of any triangle is `180^@` and there are two triangles in a quadrilateral, the sum of the angles for each quadrilateral is `360^@`.

Let’s start by examining the group of quadrilaterals that have two pairs of parallel sides. These quadrilaterals are called parallelogramsA quadrilateral with two pairs of parallel sides. They take a variety of shapes, but one classic example is shown below.

Imagine extending the pairs of opposite sides. They would never intersect because they are parallel. Notice, also, that the opposite angles of a parallelogram are congruent, as are the opposite sides. (Remember that “congruent” means “the same size.”) The geometric symbol for congruent is `~=`, so you can write `angleA~=angleC` and `angleB~=angleD`. The parallel sides are also the same length: `bar(AB)~=bar(DC)` and `bar(BC)~=bar(AD)`. These relationships are true for all parallelograms.

There are two special cases of parallelograms that will be familiar to you from your earliest experiences with geometric shapes. The first special case is called a rectangleA quadrilateral with two pairs of parallel sides and four right angles.. By definition, a rectangle is a parallelogram because its pairs of opposite sides are parallel. A rectangle also has the special characteristic that all of its angles are right angles; all four of its angles are congruent.

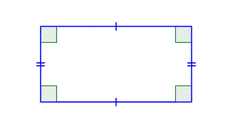
The other special case of a parallelogram is a special type of rectangle, a squareA quadrilateral whose sides are all congruent and which has four right angles.. A square is one of the most basic geometric shapes. It is a special case of a parallelogram that has four congruent sides and four right angles.

A square is also a rectangle because it has two sets of parallel sides and four right angles. A square is also a parallelogram because its opposite sides are parallel. So, a square can be classified in any of these three ways, with “parallelogram” being the least specific description and “square,” the most descriptive.

Another quadrilateral that you might see is called a rhombusA quadrilateral with four congruent sides.. All four sides of a rhombus are congruent. Its properties include that each pair of opposite sides is parallel, also making it a parallelogram.

In summary, all squares are rectangles, but not all rectangles are squares. All rectangles are parallelograms, but not all parallelograms are rectangles. And all of these shapes are quadrilaterals.

The diagram below illustrates the relationship between the different types of quadrilaterals.

You can use the properties of parallelograms to solve problems. Consider the example that follows.

There is another special type of quadrilateral. This quadrilateral has the property of having only one pair of opposite sides that are parallel. Here is one example of a trapezoidA quadrilateral with one pair of parallel sides..

Notice that `bar(XY)text(||)bar(WZ)`, and that `bar(WX)` and `bar(ZY)` are not parallel. You can easily imagine that if you extended sides `bar(WX)` and `bar(ZY)`, they would intersect above the figure.

If the non-parallel sides of a trapezoid are congruent, the trapezoid is called an isosceles trapezoidA trapezoid with one pair of parallel sides and another pair of opposite sides that are congruent.. Like the similarly named triangle that has two sides of equal length, the isosceles trapezoid has a pair of opposite sides of equal length. The other pair of opposite sides is parallel. Below is an example of an isosceles trapezoid.

In this trapezoid `ABCD`, `bar(BC)text(||)bar(AD)` and `bar(AB)~=bar(CD)`.

You can use the properties of quadrilaterals to solve problems involving trapezoids. Consider the example below.

The table below summarizes the special types of quadrilaterals and some of their properties.

A quadrilateral is a mathematical name for a four-sided polygon. Parallelograms, squares, rectangles, and trapezoids are all examples of quadrilaterals. These quadrilaterals earn their distinction based on their properties, including the number of pairs of parallel sides they have and their angle and side measurements.