The Pythagorean Theorem

Learning Objectives

Introduction

A long time ago, a Greek mathematician named PythagorasA Greek philosopher and mathematician who lived in the 6th Century B.C. discovered an interesting property about right trianglesA triangle containing a right angle.: the sum of the squares of the lengths of each of the triangle’s legsIn a right triangle, one of the two sides creating a right angle. is the same as the square of the length of the triangle’s hypotenuseThe side opposite the right angle in any right triangle. The hypotenuse is the longest side of any right triangle.. This property, which has many applications in science, art, engineering, and architecture, is now called the Pythagorean TheoremThe formula that relates the lengths of the sides of any right triangle: `a^2`+`b^2`=`c^2`, where `c` is the hypotenuse, and `a` and `b` are the legs of the right triangle. .

Let’s take a look at how this theorem can help you learn more about the construction of triangles. And the best part is you don’t even have to speak Greek to apply Pythagoras’ discovery.

The Pythagorean Theorem

Pythagoras studied right triangles, and the relationships between the legs and the hypotenuse of a right triangle, before deriving his theory.

An image shows a right triangle with base a labeled leg, height b also labeled leg, and hypotenuse c labeled hypotenuse.

The Pythagorean Theorem

If `a` and `b` are the lengths of the legs of a right triangle and `c` is the length of the hypotenuse, then the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse.

 

This relationship is represented by the formula: `a^2+b^2=c^2`

In the box above, you may have noticed the word “square,” as well as the small `2`s to the top right of the letters in `a^2+b^2=c^2`. To square a number means to multiply it by itself. So, for example, to square the number `5` you multiply `5 * 5`, and to square the number `12`, you multiply `12 * 12`. Some common squares are shown in the table below.

Number

Number Times Itself

Square

`1`

`1^2 = 1 * 1`

`1`

`2`

`2^2 = 2 * 2`

`4`

`3`

`3^2 = 3 * 3`

`9`

`4`

`4^2 = 4 * 4`

`16`

`5`

`5^2 = 5 * 5`

`25`

`10`

`10^2 = 10 * 10`

`100`

When you see the equation `a^2+b^2=c^2`, you can think of this as “the length of side `a` times itself, plus the length of side `b` times itself is the same as the length of side `c` times itself.”

Let’s try out all of the Pythagorean Theorem with an actual right triangle.

An image shows a right triangle with the base leg labeled A equals 3, the other leg labeled B equals 4, and the hypotenuse labeled C equals 5. Three equations are shown next to the image. The first equation is the Pythagorean Theorem formula: A squared plus B squared equals C squared. The second equation has measurements from the triangle plugged into the formula: 3 squared plus 4 squared equals 5 squared. The third equation shows the squaring calculations performed: 9 plus 16 equals 25.

This theorem holds true for this right triangle: the sum of the squares of the lengths of both legs is the same as the square of the length of the hypotenuse. And, in fact, it holds true for all right triangles.

The Pythagorean Theorem can also be represented in terms of area. In any right triangle, the area of the square drawn from the hypotenuse is equal to the sum of the areas of the squares that are drawn from the two legs. You can see this illustrated below in the same `3`-`4`-`5` right triangle.

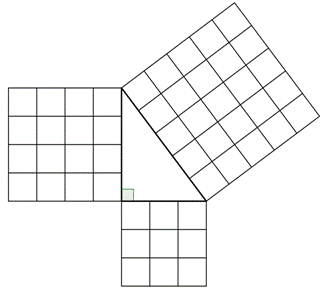
An illustration shows the original side labeled 3 with a 3-by-3 grid to represent 3 squared, or 9. It shows the original side labeled 4 with a 4-by-4 grid to represent 4 squared, or 16. It shows the original side labeled 5 with a 5-by-5 to represent 5 squared, or 25.

Note that the Pythagorean Theorem only works with right triangles.

Finding the Length of the Hypotenuse

You can use the Pythagorean Theorem to find the length of the hypotenuse of a right triangle if you know the length of the triangle’s other two sides, called the legs. Put another way, if you know the lengths of `a` and `b`, you can find `c`.

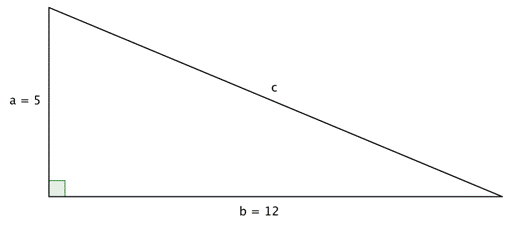
An image shows a right triangle. Leg a is 5, leg b is 12, and the hypotenuse, c, does not have a measurement.

In the triangle above, you are given measures for legs `a` and `b`: `5` and `12`, respectively. You can use the Pythagorean Theorem to find a value for the length of `c`, the hypotenuse.

`a^2+b^2=c^2`

The Pythagorean Theorem

`(5)^2+(12)^2=c^2`

Substitute known values for `a` and `b`.

`25+144=c^2`

Evaluate.

`169=c^2`

Simplify. To find the value of `c`, think about a number that, when multiplied by itself, equals `169`. Does `10` work? How about `11`? Does `12`? `13`? (You can use a calculator to multiply if the numbers are unfamiliar.)

`13 = c`

The square root of `169` is `13`.

Using the formula, you find that the length of `c`, the hypotenuse, is `13`.

In this case, you did not know the value of `c`, you were given the square of the length of the hypotenuse, and had to figure it out from there. When you are given an equation like `169=c^2` and are asked to find the value of `c`, this is called finding the square root of a number. (Notice you found a number, `c`, whose square was `169`.)

Finding a square root takes some practice, but it also takes knowledge of multiplication, division, and a little bit of trial and error. Look at the table below.

Number `x`

Number `y` which, when multiplied by itself, equals number `x`

Square root `y`

`1`

`1 * 1`

`1`

`4`

`2 * 2`

`2`

`9`

`3 * 3`

`3`

`16`

`4 * 4`

`4`

`25`

`5 * 5`

`5`

`100`

`10 * 10`

`10`

It is a good habit to become familiar with the squares of the numbers from `0` through `10`, as these arise frequently in mathematics. If you can remember those square numbers, or if you can use a calculator to find them, then finding many common square roots will be just a matter of recall.

For which of these triangles is `(3)^2+(3)^2=r^2`?

 

A)

The image shows an obtuse triangle with sides R, S, and T. Side S equals 3, side T equals 3, and side R does not have a measurement.

 

B)

The image shows a right triangle with sides R, S, and T. Side S equals 3, side T equals 3, and side R does not have a measurement.

 

C)

The image shows an equilateral triangle with sides R, S, and T. Side S equals 3, side T equals 3, and side R does not have a measurement.

 

D)

The image shows an acute triangle with sides R, S, and T. Side S equals 3, side T equals 3, and side R does not have a measurement.

 

+ 

Show/Hide Answer

 

Finding the Length of a Leg

You can use the same formula to find the length of a right triangle’s leg if you are given measurements for the lengths of the hypotenuse and the other leg. Consider the example below.

Example

Problem

 

 

 

 

 

 

 

Find the length of side `a` in the triangle below. Use a calculator to estimate the square root to one decimal place.

The image shows a right triangle with sides A and B, and hypotenuse C. Side B equals 6, hypotenuse C equals 7, and side A does not have a measurement.

 

`a=text(?)`

`b = 6`

`c = 7`

In this right triangle, you are given the measurements for the hypotenuse, `c`, and one leg, `b`. The hypotenuse is always opposite the right angle and it is always the longest side of the triangle.

 

`a^2+b^2=c^2`

`a^2+6^2=7^2`

To find the length of leg `a`, substitute the known values into the Pythagorean Theorem.

 

`a^2+36=49`

`a^2=13`

Solve for `a^2`. Think: what number, when added to `36`, gives you `49`?

 

`a~~3.6`

Use a calculator to find the square root of `13`. The calculator gives an answer of `3.6055`…, which you can round to `3.6`. (Since you are approximating, you use the symbol `~~`.)

Answer

`a~~3.6`

 

 

Which of the following correctly uses the Pythagorean Theorem to find the missing side, `x`?  

 

The image shows a right triangle. One leg is 8, the hypotenuse is 10, and the other leg is labeled X.

 

A) `8^2+10^2=x^2`

 

B) `x + 8 = 10`

 

C) `x^2+8^2=10^2`

 

D) `x^2+10^2=8^2`

 

+ 

Show/Hide Answer

 

Using the Theorem to Solve Real World Problems

The Pythagorean Theorem is perhaps one of the most useful formulas you will learn in mathematics because there are so many applications of it in real-world settings. Architects and engineers use this formula extensively when building ramps, bridges, and buildings. Look at the following examples.

Example

Problem

 

 

 

 

 

 

 

 

 

 

The owners of a house want to convert a stairway leading from the ground to their back porch into a ramp. The porch is `3` feet off the ground and, due to building regulations, the ramp must start `12` feet away from the base of the porch. How long will the ramp be?

 

Use a calculator to find the square root, and round the answer to the nearest tenth.

 

 

 

To solve a problem like this one, it often makes sense to draw a simple diagram showing where the legs and hypotenuse of the triangle lie.

 

A diagram shows that the porch, the ground, and the new ramp form a right triangle. The ground is perpendicular to the porch, forming a right angle; this leg is labeled A equals 3. The leg from the ground directly below the porch to the ground at the end of the new ramp is labeled B equals 12. The hypotenuse that goes from the porch to the ground where the new ramp ends is labeled C.

 

`a = 3`

`b = 12`

`c=?`

Identify the legs and the hypotenuse of the triangle. You know that the triangle is a right triangle since the ground and the raised portion of the porch are perpendicular. This means you can use the Pythagorean Theorem to solve this problem. Identify `a`, `b`, and `c`.

 

`a^2+b^2=c^2`

`3^2+12^2=c^2`

`9+144=c^2`

`153=c^2`

Use the Pythagorean Theorem to find the length of `c`.

 

`12.4 = c`

Use your calculator to find `c`. The square root of `153` is `12.369`…, so you can round that to `12.4`.

Answer

The ramp will be `12.4` feet long.

 

 

Example

Problem

 

 

 

A sailboat has a large sail in the shape of a right triangle. The longest edge of the sail measures `17` yards and the bottom edge of the sail is `8` yards. How tall is the sail?

 

An image shows that one leg of a right triangle is 8 yards. The hypotenuse is 17 yards. The leg labeled “A” does not have a measurement.

Draw an image to help you visualize the problem. In a right triangle, the hypotenuse will always be the longest side, so here it must be `17` yards. The problem also tells you that the bottom edge of the triangle is `8` yards.

 

`a^2+b^2=c^2`

`a^2+8^2=17^2`

`a^2+64=289`

`a^2=225`

Set up the Pythagorean Theorem.

 

`a = 15`

`15 * 15 = 225`, so `a=15`.

Answer

The height of the sail is `15` yards.

Summary

The Pythagorean Theorem states that in any right triangle, the sum of the squares of the lengths of the triangle’s legs is the same as the square of the length of the triangle’s hypotenuse. This theorem is represented by the formula `a^2+b^2=c^2`. Put simply, if you know the lengths of two sides of a right triangle, you can apply the Pythagorean Theorem to find the length of the third side. Remember, this theorem only works for right triangles.