Triangles

Learning Objectives

Introduction

Geometric shapes, also called figures, are an important part of the study of geometry. The triangleA polygon with three sides. is one of the basic shapes in geometry. It is the simplest shape within a classification of shapes called polygonsA closed plane figure with three or more straight sides.. All triangles have three sides and three angles, but they come in many different shapes and sizes. Within the group of all triangles, the characteristics of a triangle’s sides and angles are used to classify it even further. Triangles have some important characteristics, and understanding these characteristics allows you to apply the ideas in real-world problems.

Classifying and Naming Triangles

A polygon is a closed plane figure with three or more straight sides. Polygons each have a special name based on the number of sides they have. For example, the polygon with three sides is called a triangle because “tri” is a prefix that means “three.” Its name also indicates that this polygon has three angles. The prefix “poly” means many.

The table below shows and describes three classifications of triangles. Notice how the types of angles in the triangle are used to classify the triangle.

Name of Triangle

Picture of Triangle

Description

Acute TriangleA triangle with three angles that each measure between `0^@` and `90^@`.

 

The image shows a triangle with three acute angles.

 

A triangle with `3` acute angles (`3` angles measuring between `0^@` and `90^@`).

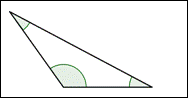
Obtuse TriangleA triangle with one angle that measures between `90^@` and `180^@`.

 

The image shows a triangle with one obtuse angle and two acute angles.

 

A triangle with `1` obtuse angle (`1` angle measuring between `90^@` and `180^@`).

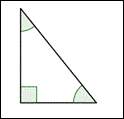
Right TriangleA triangle containing a right angle.

 

The image shows a triangle. One of the angles formed is 90 degrees. The other two angles are acute.

 

A triangle containing one right angle (`1` angle that measures `90^@`). Note that the right angle is shown with a corner mark and does not need to be labeled `90^@`.

The sum of the measures of the three interior angles of a triangle is always `180^@`. This fact can be applied to find the measure of the third angle of a triangle, if you are given the other two. Consider the examples below.

Example

Problem

 

A triangle has two angles that measure `35^@` and `75^@`. Find the measure of the third angle.

 

`35^@+75^@+x=180^@`

The sum of the three interior angles of a triangle is `180^@`.

 

`110^@+x=180^@`

 

Find the value of `x`.

 

`x=180^@-110^@`

`x=70^@`

 

Answer

The third angle of the triangle measures `70^@`.

 
       

Example

Problem

 

One of the angles in a right triangle measures `57^@`.

Find the measurement of the third angle.

 

`57^@+90^@+x=180^@`

The sum of the three angles of a triangle is always `180^@`. One of the angles has a measure of `90^@` as it is a right triangle.

 

`147^@+x=180^@`

Simplify.

 

`x=180^@-147^@`

`x = 33^@`

 

Find the value of `x`.

Answer

The third angle of the right triangle measures `33^@`.

 
       

There is an established convention for naming triangles. The labels of the vertices of the triangle, which are generally capital letters, are used to name a triangle.

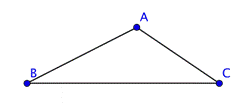
The image shows an acute triangle. The vertices are labeled A, B, and C.

You can call this triangle ABC or `triangleABC` since `A`, `B`, and `C` are vertices of the triangle. When naming the triangle, you can begin with any vertex. Then keep the letters in order as you go around the polygon. The triangle above could be named in a variety of ways: `triangleABC`, or `triangleCBA`. The sides of the triangle are line segments `AB`, `AC`, and `CB`.

Just as triangles can be classified as acute, obtuse, or right based on their angles, they can also be classified by the length of their sides. Sides of equal length are called congruentHaving the same size and shape. sides. While we designate a segment joining points `A` and `B` by the notation `bar(AB)`, we designate the length of a segment joining points `A` and `B` by the notation `AB` without a segment bar over it. The length `AB` is a number, and the segment `bar(AB)`  is the collection of points that make up the segment. 

Mathematicians show congruency by putting a hash mark symbol through the middle of sides of equal length. If the hash mark is the same on one or more sides, then those sides are congruent. If the sides have different hash marks, they are not congruent. The table below shows the classification of triangles by their side lengths.

Name of Triangle

Picture of Triangle

Description

Equilateral TriangleA triangle with `3` equal sides.

 

The image shows an equilateral triangle. All three sides of the triangle are equal, indicated by a single hash mark in the middle of each side.

 

A triangle whose three sides have the same length. These sides of equal length are called congruent sides.

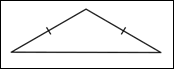
Isosceles TriangleA triangle with `2` equal sides.

 

The image shows an isosceles triangle. Two sides of the triangle are equal, indicated by a single hash mark in the middle of each of the two equal sides.

 

A triangle with exactly two congruent sides.

Scalene TriangleA triangle in which all three sides are a different length.

 

The image shows a scalene triangle with three sides of different lengths.

 

A triangle in which all three sides are a different length.

To describe a triangle even more specifically, you can use information about both its sides and its angles. Consider this example.

Example

Problem

 

 

 

 

 

 

 

Classify the triangle below.

 

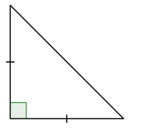
The image shows a right triangle. It has two equal sides, indicated by a single hash mark in the middle of each of those two sides.

 

 

The image shows a right triangle. The right-angle symbol is circled in red to highlight that it is a right angle. The triangle has two equal sides, indicated by a single hash mark in the middle of each of those two sides.

Notice what kind of angles the triangle has. Since one angle is a right angle, this is a right triangle.

 

An image shows a right triangle. It has two equal sides, indicated by a single hash mark in the middle of each of those two sides.

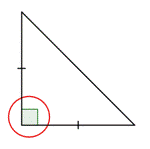
Notice the lengths of the sides. Are there congruence marks or other labels?

 

The congruence marks tell us there are two sides of equal length. So, this is an isosceles triangle.

Answer

This is an isosceles right triangle.

 

Classify the triangle shown below.

 

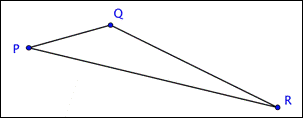
The image shows a triangle with no equal sides and one angle (angle Q) that is between 90 degrees and 180 degrees. The vertices are labeled P, Q, and R.

 

A) acute scalene

 

B) right isosceles

 

C) obtuse scalene

 

D) obtuse isosceles

 

+ 

Show/Hide Answer

 

Identifying Congruent and Similar Triangles

Two triangles are congruent if they are exactly the same size and shape. In congruent triangles, the measures of corresponding anglesAngles of separate figures that are in the same position within each figure. and the lengths of corresponding sidesSides of separate figures that are opposite corresponding angles. are equal. Consider the two triangles shown below:

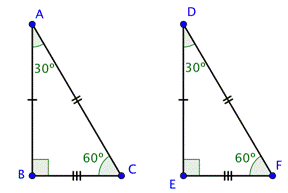
The image shows two congruent right triangles, A B C and D E F. Angle A B C and angle D E F are 90-degree angles. Angle B C A and angle E F D are labeled “60 degrees.” Angle C A B and angle F D A are labeled “30 degrees.” A B and D E are corresponding sides, indicated by a single hash mark in the middle of each line. A C and D F are corresponding sides, indicated by two hash marks in the middle of each line. B C and E F are corresponding sides, indicated by three hash marks in the middle of each line.

Since both `angleB` and `angleE` are right angles, these triangles are right triangles. Let’s call these two triangles `triangleABC` and `triangleDEF`. These triangles are congruent if every pair of corresponding sides has equal lengths and every pair of corresponding angles has the same measure.

The corresponding sides are opposite the corresponding angles.

A double headed arrow means “corresponds to”

`angleBharrangleE`

`angleAharrangleD`

`angleCharrangleF`

`bar(AB)harrbar(DE)`

`bar(AC)harrbar(DF)`

`bar(BC)harrbar(EF)`

 `triangleABC` and `triangleDEF` are congruent triangles as the corresponding sides and corresponding angles are equal.

Let’s take a look at another pair of triangles. Below are the triangles `triangleABC` and `triangleRST`.

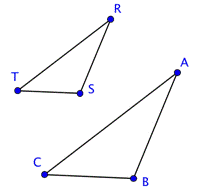
The image shows two similar triangles, A B C and R S T, that have the same shape but are different sizes. R S T is smaller than A B C.

These two triangles are surely not congruent because `triangleRST` is clearly smaller in size than `triangleABC`. But, even though they are not the same size, they do resemble one another. They are the same shape. The corresponding angles of these triangles look like they might have the same exact measurement, and if they did they would be congruent angles and we would call the triangles similar triangles.

Congruent angles are marked with hash marks, just as congruent sides are.

The image shows two similar triangles that have the same shape but are different sizes. One is smaller than the other. The measurements for the corresponding angles are 40 degrees, 110 degrees, and 30 degrees.

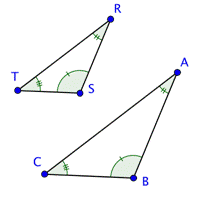
The image shows two similar triangles, A B C and R S T, that have the same shape but are different sizes. R S T is smaller than A B C. The corresponding angles are indicated by single, double, or triple hash marks, representing congruency.

Image showing angle measurements of both triangles.

Image showing triangles `ABC` and `RST` using hash marks to show angle congruency.

We can also show congruent angles by using multiple bands within the angle, rather than multiple hash marks on one band. Below is an image using multiple bands within the angle.

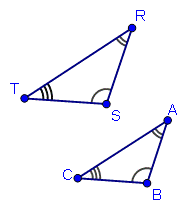
The image shows two similar triangles, A B C and R S T, that have the same shape but are different sizes. Angle S and angle B are congruent, indicated by a single band. Angle A and angle R are congruent, indicated by a double band. Angle T and angle C are congruent, indicated by a triple band.

Image showing triangles `ABC` and `RST` using bands to show angle congruency. 

If the corresponding angles of two triangles have the same measurements, they are called similarHaving the same shape but not necessarily the same size. triangles. This name makes sense because they have the same shape, but not necessarily the same size. When a pair of triangles is similar, the corresponding sides are proportional to one another. That means that there is a consistent scale factor that can be used to compare the corresponding sides. In the previous example, the side lengths of the larger triangle are all `1.4` times the length of the smaller. So, similar triangles are proportional to one another.

Just because two triangles look similar does not mean they are similar triangles in the mathematical sense of the word. Checking that the corresponding angles have equal measure is one way of being sure the triangles are similar.

Corresponding Sides of Similar Triangles

There is another method for determining similarity of triangles that involves comparing the ratios of the lengths of the corresponding sides.

If the ratios of the pairs of corresponding sides are equal, the triangles are similar.

Consider the two triangles below.

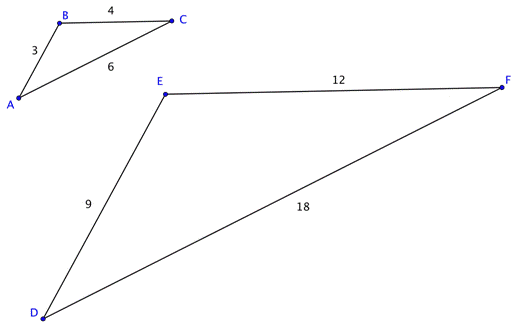
The image shows two similar triangles, A B C and D E F. Triangle A B C is smaller than triangle D E F. In triangle A B C, side A B is 3, side B C is 4, and side C A is 6. In triangle D E F, side D E is 9, side E F is 12, and side F D is 18.

`triangleABC` is not congruent to `triangleDEF` because the side lengths of `triangleDEF` are longer than those of `triangleABC`. So, are these triangles similar? If they are, the corresponding sides should be proportional.

Since these triangles are oriented in the same way, you can pair the left, right, and bottom sides: `bar(AB)` and `bar(DE)`, `bar(BC)` and `bar(EF)`, `bar(AC)` and `bar(DE)`. (You might have called these the two shortest sides, the two longest sides, and the two leftover sides and arrived at the same ratios). Now we will look at the ratios of their lengths.

`(AB)/(DE)=(BC)/(EF)=(AC)/(DF)`

Substituting the side length values into the proportion, you see that it is true:

`3/9=4/12=6/18`

If the corresponding sides are proportional, then the triangles are similar. Triangles `ABC` and `DEF` are similar, but not congruent.

Let’s use this idea of proportional corresponding sides to determine whether two more triangles are similar.

Example

Problem

 

 

 

 

 

 

 

 

 

 

 

Determine if the triangles below are similar by seeing if their corresponding sides are proportional.

 

The image shows two similar triangles, A B C and D E F. Triangle A B C is larger than triangle D E F. In triangle A B C, side A B is 6, side B C is 14, and side C A is 10. In triangle D E F, side D E is 3, side E F is 7, and side F D is 5.

 

`bar(CA)harrbar(FD)`

`bar(AB)harrbar(DE)`

`bar(BC)harrbar(EF)`

First determine the corresponding sides, which are opposite corresponding angles.

 

`(CA)/(FD)=(AB)/(DE)=(BC)/(EF)`

Write the corresponding side lengths as ratios.

 

 

`10/5=6/3=14/7`

 

`2 = 2 = 2`

Substitute the side lengths into the ratios, and determine if the ratios of the corresponding sides are equivalent. They are, so the triangles are similar.

Answer

`triangleABC` and `triangleDEF` are similar.

 
       

The mathematical symbol `~` means “is similar to.” So, you can write `triangleABC` is similar to `triangleDEF` as `triangleABC~triangleDEF`.

Determine whether the two triangles are similar, congruent, or neither.

 

An image shows two triangles, A B C and D E F. In triangle A B C, all the sides are 5. In triangle D E F, two sides are 6.5 and one side is 5.

 

A) `triangleABC` and `triangleDEF` are congruent.

 

B) `triangleABC` and `triangleDEF` are similar.

 

C) `triangleABC` and `triangleDEF` are similar and congruent.

 

D) `triangleABC` and `triangleDEF` are neither similar nor congruent.

 

+ 

Show/Hide Answer

 

Finding Missing Measurements in Similar Triangles

You can find the missing measurements in a triangle if you know some measurements of a similar triangle. Let’s look at an example.

Example

Problem

 

 

 

 

 

 

 

 

 

 

 

 

 

 `triangleABC` and `triangleXYZ`  are similar triangles.

What is the length of side `BC`?

 

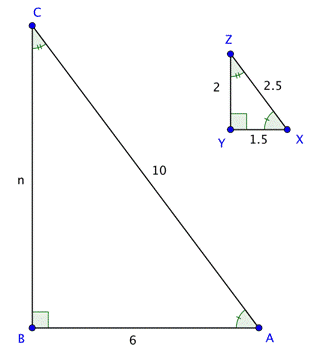
An image shows two similar triangles, A B C and X Y Z. Triangle A B C is larger than triangle X Y Z. Single hash marks indicate that angle A is congruent to angle X. Double hash marks indicate that angle C is congruent with angle Z. Angle B and angle Y are marked as right angles. In triangle A B C, side A B is 6, side B C is labeled with the variable “n,” and side CA is 10. In triangle X Y Z, side X Y is labeled 1.5, side Y Z is 2, and side Z X is 2.5.

 

`(BC)/(YZ)=(AB)/(XY)`

 

 

In similar triangles, the ratios of corresponding sides are proportional. Set up a proportion of two ratios, one that includes the missing side.

 

`n/2=6/1.5`

Substitute in the known side lengths for the side names in the ratio. Let the unknown side length be `n`.

 

`2*6=1.5*n`

`12=1.5n`

`8=n`

 

Solve for `n` using cross multiplication.

Answer

The missing length of side `BC` is `8` units.

This process is fairly straightforward, but be careful that your ratios represent corresponding sides, recalling that corresponding sides are opposite corresponding angles.

Solving Application Problems Involving Similar Triangles

Applying knowledge of triangles, similarity, and congruence can be very useful for solving problems in real life. Just as you can solve for missing lengths of a triangle drawn on a page, you can use triangles to find unknown distances between locations or objects.

Let’s consider the example of two trees and their shadows. Suppose the sun is shining down on two trees, one that is `6` feet tall and the other whose height is unknown. By measuring the length of each shadow on the ground, you can use triangle similarity to find the unknown height of the second tree.

First, let’s figure out where the triangles are in this situation! The trees themselves create one pair of corresponding sides. The shadows cast on the ground are another pair of corresponding sides. The third side of these imaginary similar triangles runs from the top of each tree to the tip of its shadow on the ground. This is the hypotenuse of the triangle.

If you know that the trees and their shadows form similar triangles, you can set up a proportion to find the height of the tree.

Example

Problem

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

When the sun is at a certain angle in the sky, a `6`-foot tree will cast a `4`-foot shadow. How tall is a tree that casts an `8`-foot shadow?

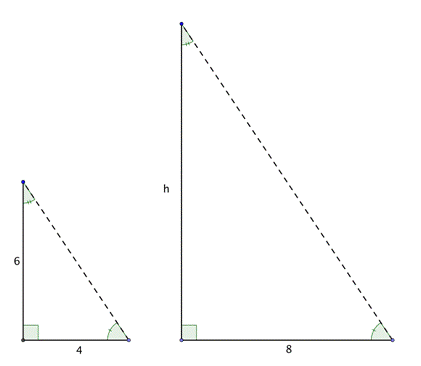
An image shows two similar right triangles. The first triangle represents the 6-foot tree that casts a 4-foot shadow; the legs of the triangle are labeled 6 and 4. The second triangle represents the tree with an unknown height that casts an 8-foot shadow; the legs of the triangle are labeled H and 8.

 

 

`text(Tree 1)/text(Tree 2)=text(Shadow 1)/text(Shadow 2)` 

The angle measurements are the same, so the triangles are similar triangles. Since they are similar triangles, you can use proportions to find the size of the missing side.

 

Set up a proportion comparing the heights of the trees and the lengths of their shadows.

 

`6/h=4/8`

Substitute in the known lengths. Call the missing tree height `h`.

 

`6*8=4h`

`48=4h`

`12=h`

Solve for `h` using cross-multiplication.

Answer

The tree is `12` feet tall.

 
       

Summary

Triangles are one of the basic shapes in the real world. Triangles can be classified by the characteristics of their angles and sides, and triangles can be compared based on these characteristics. The sum of the measures of the interior angles of any triangle is `180^@`. Congruent triangles are triangles of the same size and shape. They have corresponding sides of equal length and corresponding angles of the same measurement. Similar triangles have the same shape, but not necessarily the same size. The lengths of their sides are proportional. Knowledge of triangles can be a helpful in solving real-world problems.