Properties of Angles
Imagine two separate and distinct lines on a plane. There are two possibilities for these lines: they will either intersect at one point, or they will never intersect. When two lines intersect, four angles are formed. Understanding how these angles relate to each other can help you figure out how to measure them, even if you only have information about the size of one angle.
Parallel linesTwo or more lines that lie in the same plane but which never intersect. are two or more lines that never intersect. Likewise, parallel line segments are two line segments that never intersect even if the line segments were turned into lines that continued forever. Examples of parallel line segments are all around you, in the two sides of this page and in the shelves of a bookcase. When you see lines or structures that seem to run in the same direction, never cross one another, and are always the same distance apart, there’s a good chance that they are parallel.
Perpendicular linesTwo lines that lie in the same plane and intersect at a `90^@` angle. are two lines that intersect at a `90^@` (right) angle. And perpendicular line segments also intersect at a `90^@` (right) angle. You can see examples of perpendicular lines everywhere as well: on graph paper, in the crossing pattern of roads at an intersection, to the colored lines of a plaid shirt. In our daily lives, you may be happy to call two lines perpendicular if they merely seem to be at right angles to one another. When studying geometry, however, you need to make sure that two lines intersect at a `90^@` angle before declaring them to be perpendicular.
The image below shows some parallel and perpendicular lines. The geometric symbol for parallel is `"||"`, so you can show that `overset(harr)(AB)text(||)overset(harr)(CD)`. Parallel lines are also often indicated by the marking >> on each line (or just a single `>` on each line). Perpendicular lines are indicated by the symbol `_|_`, so you can write `overset(harr)(WX)_|_overset(harr)(YZ)`.


If two lines are parallel, then any line that is perpendicular to one line will also be perpendicular to the other line. Similarly, if two lines are both perpendicular to the same line, then those two lines are parallel to each other. Let’s take a look at one example and identify some of these types of lines.
|
Example |
||
|
Problem
|
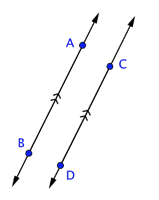
Identify a set of parallel lines and a set of perpendicular lines in the image below.
|
|
|
|
|
Parallel lines never meet, and perpendicular lines intersect at a right angle.
`overset(harr)(AB)` and `overset(harr)(CD)` do not intersect in this image, but if you imagine extending both lines, they will intersect soon. So, they are neither parallel nor perpendicular. |
|
|
|
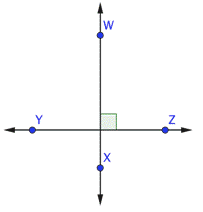
`overset(harr)(AB)` is perpendicular to both `overset(harr)(WX)` and `overset(harr)(YZ)`, as indicated by the right-angle marks at the intersection of those lines. |
|
|
|
Since `overset(harr)(AB)` is perpendicular to both lines, then `overset(harr)(WX)` and `overset(harr)(YZ)` are parallel. |
|
Answer |
`overset(harr)(WX)text(||)overset(harr)(YZ)` `overset(harr)(AB)_|_overset(harr)(WX), overset(harr)(AB)_|_overset(harr)(YZ)` |
|
|
Which statement most accurately represents the image below?
A) `overset(harr)(EF)text(||)overset(harr)(GH)`
B) `overset(harr)(AB)_|_overset(harr)(EG)`
C) `overset(harr)(FH)text(||)overset(harr)(EG)`
D) `overset(harr)(AB)text(||)overset(harr)(FH)`
|
Understanding how parallel and perpendicular lines relate can help you figure out the measurements of some unknown angles. To start, all you need to remember is that perpendicular lines intersect at a `90^@` angle, and that a straight angle measures `180^@`.
The measure of an angle such as `angleA` is written as `mangleA`. Look at the example below. How can you find the measurements of the unmarked angles?
|
Example |
||
|
Problem
|
Find the measurement of `/_IJF`.
|
|
|
|
|
Only one angle, `angleHJM`, is marked in the image. Notice that it is a right angle, so it measures `90^@`. `angleHJM` is formed by the intersection of lines `overset(harr)(IM)` and `overset(harr)(HF)`. Since `overset(harr)(IM)` is a line, `angleIJM` is a straight angle measuring `180^@`. |
|
|
|
You can use this information to find the measurement of `angleHJI`: `mangleHJM+mangleHJI=mangleIJM` `90^@+mangleHJI=180^@` `mangleHJI=90^@` |
|
|
|
Now use the same logic to find the measurement of `angleIJF`. `angleIJF` is formed by the intersection of lines `overset(harr)(IM)` and `overset(harr)(HF)`. Since `overset(harr)(HF)` is a line, `angleHJF` will be a straight angle measuring `180^@`. |
|
|
|
You know that `angleHJI` measures `90^@`. Use this information to find the measurement of `angleIJF`: `mangleHJI+mangleIJF=mangleHJF` `90^@+mangleIJF=180^@` `mangleIJF=90^@` |
|
Answer |
`mangleIJF=90^@` |
|
In this example, you may have noticed that angles `angleHJI`, `angleIJF`, and `angleHJM` are all right angles. (If you were asked to find the measurement of `angleFJM`, you would find that angle to be `90^@`, too.) This is what happens when two lines are perpendicular: the four angles created by the intersection are all right angles.
Not all intersections happen at right angles, though. In the example below, notice how you can use the same technique as shown above (using straight angles) to find the measurement of a missing angle.
|
Example |
||
|
Problem
|
Find the measurement of `angleDAC`.
|
|
|
|
|
This image shows the line `overset(harr)(BC)` and the ray `overset(rarr)(AD)` intersecting at point `A`. The measurement of `angleBAD` is `135^@`. You can use straight angles to find the measurement of `angleDAC`. |
|
|
|
`angle BAC` is a straight angle, so it measures `180^@`. |
|
|
|
Use this information to find the measurement of `angle DAC`. `mangleBAD+mangleDAC=mangleBAC` `135^@+mangleDAC=180^@` `mangleDAC=45^@` |
|
Answer
|
`mangleDAC=45^@`
|
|
|
Find the measurement of `angleCAD`.
A) `43^@`
B) `137^@`
C) `147^@`
D) `317^@`
|
In the example above, `mangleBAC` and `mangleDAC` add up to `180^@`. Two angles whose measures add up to `180^@` are called supplementary anglesTwo angles whose measurements add up to `180^@`. . There’s also a term for two angles whose measurements add up to `90^@`; they are called complementary anglesTwo angles whose measurements add up to `90^@`. .
One way to remember the difference between the two terms is that “corner” and “complementary” each begin with c (a `90^@` angle looks like a corner), while straight and “supplementary” each begin with s (a straight angle measures `180^@`).
If you can identify supplementary or complementary angles within a problem, finding missing angle measurements is often simply a matter of adding or subtracting.
|
Example |
||||
|
Problem
|
Two angles are supplementary. If one of the angles measures `48^@`, what is the measurement of the other angle? |
|||
|
|
`mangleA+mangleB=180^@` |
Two supplementary angles make up a straight angle, so the measurements of the two angles will be `180^@`. |
||
|
|
`48^@+mangleB=180^@` `mangleB=180^@-48^@` `mangleB=132^@` |
You know the measurement of one angle. To find the measurement of the second angle, subtract `48^@` from `180^@`. |
||
|
Answer |
The measurement of the other angle is `132^@`. |
|||
|
Example |
||
|
Problem
|
Find the measurement of `angleAXZ`.
|
|
|
|
|
This image shows two intersecting lines, `overset(harr)(AB)` and `overset(harr)(YZ)`. They intersect at point `X`, forming four angles.
Angles `angleAXY` and `angleAXZ` are supplementary because together they make up the straight angle `angleYXZ`. |
|
|
|
Use this information to find the measurement of `angleAXZ`. `mangleAXY+mangleAXZ=mangleYXZ` `30^@+mangleAXZ=180^@` `mangleAXZ=150^@` |
|
Answer |
`mangleAXZ=150^@` |
|
|
Example |
||
|
Problem
|
Find the measurement of `angleBAC`.
|
|
|
|
|
This image shows the line `overset(harr)(CF)` and the rays `overset(rarr)(AB` and `overset(rarr)(AD)`, all intersecting at point `A`. Angle `angleBAD` is a right angle.
Angles `angleBAC` and `angleCAD` are complementary, because together they create `angleBAD`. |
|
|
|
Use this information to find the measurement of `angleBAC`. `mangleBAC+mangleCAD=mangleBAD` `mangleBAC+50^@=90^@` `mangleBAC=40^@` |
|
Answer |
`mangleBAC=40^@` |
|
|
Example |
||
|
Problem
|
Find the measurement of `angleCAD`.
|
|
|
|
|
You know the measurements of two angles here: `angleCAB` and `angleDAE`. You also know that `mangleBAE=180^@`. |
|
|
|
Use this information to find the measurement of `angleCAD`. `mangleBAC+mangleCAD+mangleDAE=mangleBAE` `25^@+mangleCAD+75^@=180^@` `mangleCAD+100^@=180^@` `mangleCAD=80^@` |
|
Answer |
`mangleCAD=80^@` |
|
|
Which pair of angles is complementary?
A) `anglePKO` and `angleMKN`
B) `anglePKO` and `anglePKM`
C) `angle LKP` and `angle LKN`
D) `angleLKM` and `angleMKN`
|
Parallel lines do not intersect, while perpendicular lines cross at a `90^@` angle. Two angles whose measurements add up to `180^@` are said to be supplementary, and two angles whose measurements add up to `90^@` are said to be complementary. For most pairs of intersecting lines, all you need is the measurement of one angle to find the measurements of all other angles formed by the intersection.