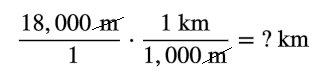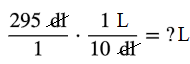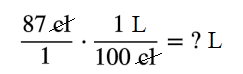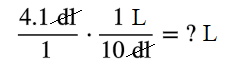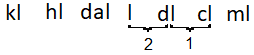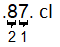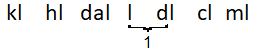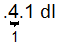Using Metric Conversions to Solve Problems
Learning Objective
- Solve application problems involving metric units of length, mass, and volume.
Introduction
Learning how to solve real-world problems using metric conversions is as important as learning how to do the conversions themselves. Mathematicians, scientists, nurses, and even athletes are often confronted with situations where they are presented with information using metric measurements, and must then make informed decisions based on that data.
To solve these problems effectively, you need to understand the context of a problem, perform conversions, and then check the reasonableness of your answer. Do all three of these steps and you will succeed in whatever measurement system you find yourself using.
Understanding Context and Performing Conversions
The first step in solving any real-world problem is to understand its context. This will help you figure out what kinds of solutions are reasonable (and the problem itself may give you clues about what types of conversions are necessary). Here is an example.
|
Example
|
|
Problem
|
In the Summer Olympic Games, athletes compete in races of the following lengths: `100` meters, `200` meters, `400` meters, `800` meters, `1500` meters, `5000` meters and `10,000` meters. If a runner were to run in all these races, how many kilometers would he run?
|
|
|
| |
`10,000` |
| |
`5,000` |
| |
`1,500` |
| |
`800` |
| |
`400` |
| |
`200` |
| `+` |
`100` |
| |
`18,000` |
|
To figure out how many kilometers he would run, you need to first add all of the lengths of the races together and then convert that measurement to kilometers.
|
|
|
`(18,000text( meters))/1*(1text( kilometer))/(1,000text( meters))=text (? kilometers)`
|
Use the factor label method and unit fractions to convert from meters to kilometers.
|
|
|
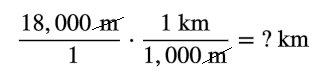
`(18,000)/1*(1text( kilometer))/(1,000)=(18,000text ( kilometers))/(1,000)`
`(18,000text( kilometers))/(1,000)=18text ( kilometers)`
|
Cancel, multiply, and solve.
|
|
Answer
|
The runner would run `18` kilometers.
|
|
This may not be likely to happen (a runner would have to be quite an athlete to compete in all of these races) but it is an interesting question to consider. The problem required you to find the total distance that the runner would run (in kilometers). The example showed how to add the distances, in meters, and then convert that number to kilometers.
An example with a different context, but still requiring conversions, is shown below.
|
Example
|
|
Problem
|
One bottle holds `295` deciliters while another one holds `28,000` milliliters. What is the difference in capacity between the two bottles?
|
|
|
`295text( deciliters)=text(? liters)`
`28,000text( milliliters)=text(? liters)`
|
The two measurements are in different units. You can convert both units to liters and then compare them.
|
|
|
`(295text( deciliters))/1*(1text( liter))/(10text( deciliters))=text(? liters)`
|
Convert deciliters to liters.
|
|
|
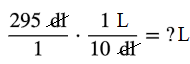
`(295)/1*(1text( liter))/(10)=(295text( liters))/10`
`(295text( liters))/10=29.5text( liters)`
|
Cancel similar units and multiply.
`295text ( deciliters)=29.5text( liters)`
|
|
|
`(28,000" milliliters")/1*(1" liter")/(1,000" milliliters")="? liters"`

`(28,000)/1*(1" liter")/(1,000)=(28,000" liters")/(1,000)`
`(28,000" liters")/(1,000)=28" liters"`
|
Convert milliliters to liters.
`28,000" milliliters"=28" liters"`
|
|
|
`29.5" liters"-28" liters" = 1.5" liters"`
|
The question asks for “difference in capacity” between the bottles.
|
|
Answer
|
There is a difference in capacity of `1.5` liters between the two bottles.
|
This problem asked for the difference between two quantities. The easiest way to find this is to convert one quantity so that both quantities are measured in the same unit, and then subtract one from the other.
|
One boxer weighs in at `85` kilograms. He is `80` dekagrams heavier than his opponent. How much does his opponent weigh?
A) `5` kilograms
B) `84.2` kilograms
C) `84.92` kilograms
D) `85.8` kilograms
A) `5` kilograms
Incorrect. Look at the unit labels. The boxer is `80` dekagrams heavier, not `80` kilograms heavier. The correct answer is `84.2` kilograms.
B) `84.2` kilograms
Correct. `80text( dekagrams) = 0.8text( kilograms)`, and `85 - 0.8 = 84.2`.
C) `84.92` kilograms
Incorrect. This would have been true if the difference in weight was `8` dekagrams, not `80` dekagrams. The correct answer is `84.2` kilograms.
D) `85.8` kilograms
Incorrect. The first boxer is `80` dekagrams heavier, not lighter than his opponent. This question asks for the opponent’s weight. The correct answer is `84.2` kilograms.
|
Checking your Conversions
Sometimes it is a good idea to check your conversions using a second method. This usually helps you catch any errors that you may make, such as using the wrong unit fractions or moving the decimal point the wrong way.
|
Example
|
|
Problem
|
A two-liter bottle contains `87` centiliters of oil and `4.1` deciliters of water. How much more liquid is needed to fill the bottle?
|
|
|
`87text( centiliters)+4.1text( deciliters )+text(?)=2text( liters)`
|
You are looking for the amount of liquid needed to fill the bottle. Convert both measurements to liters and then solve the problem.
|
|
|
`87text( centiliters)=text( ? liters)`
`(87text( centiliters))/1*(1text( liters))/(100text( centiliters))=text(? liters)`
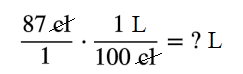
`(87)/1*(1text( liter))/(100)=(87text( liters))/100`
`(87text( liters))/100=0.87text( liters)`
|
Convert `87` centiliters to liters.
|
|
|
`4.1text( deciliters)=text(? liters)`
`(4.1text( deciliters))/1*(1text( liter))/(10text( deciliters))=text(? liters)`
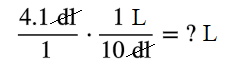
`4.1/1*(1text( liter))/10=(4.1text( liters))/10`
`(4.1text( liters))/10=0.41text( liters)`
|
Convert `4.1` deciliters to liters.
|
|
|
`87text( centiliters)+4.1text( deciliters)+text(?)=2text( liters)`
`0.87text( liter)+0.41text( liter)+text(?)=2text( liters)`
`2text( liters)-0.87text( liter)-0.41text( liter)=0.72text( liter)`
|
Subtract to find how much more liquid is needed to fill the bottle.
|
|
Answer
|
The amount of liquid needed to fill the bottle is `0.72` liter.
|
Having come up with the answer, you could also check your conversions using the quicker “move the decimal” method, shown below.
|
Example
|
|
Problem
|
A two-liter bottle contains `87` centiliters of oil and `4.1` deciliters of water. How much more liquid is needed to fill the bottle?
|
|
|
`87text( centiliters)+4.1text( deciliters)+text(?)=2text( liters)`
|
You are looking for the amount of liquid needed to fill the bottle.
|
|
|
`87text( centiliters)= ?text( liters)`
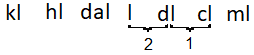
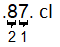
`87text( centiliters)=0.87text( liters)`
|
Convert `87` centiliters to liters.
On the chart, liters (l) are two places to the left of centiliters (cl).
Move the decimal point two places to the left in `87` centiliters.
|
|
|
`4.1text( deciliters)=text(? liters)`
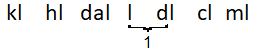
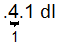
`4.1text( deciliters)=0.41text( liters)`
|
Convert `4.1` deciliters to liters.
On the chart, liter (l) is one place to the left of deciliter (dl).
Move the decimal point one place to the left in `4.1` deciliters.
|
|
|
`87text( centiliters)+4.1text( deciliters)+text(?)=2text( liters)`
`0.87text( liter)+0.41text( liter)+text(?)=2text( liters)`
`2text( liters)-0.87text( liter)-0.41text( liter)=0.72text( liter)`
|
Subtract to find how much more liquid is needed to fill the bottle.
|
|
Answer
|
The amount of liquid needed to fill the bottle is `0.72` liters.
|
The initial answer checks out. `0.72` liter of liquid is needed to fill the bottle. Checking one conversion with another method is a good practice for catching any errors in scale.
Summary
Understanding the context of real-life application problems is important. Look for words within the problem that help you identify what operations are needed, and then apply the correct unit conversions. Checking your final answer by using another conversion method (such as the “move the decimal” method, if you have used the factor label method to solve the problem) can cut down on errors in your calculations.