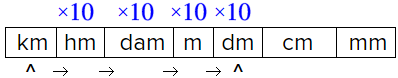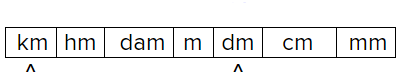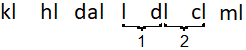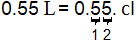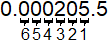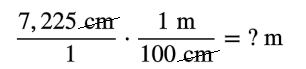Converting within the Metric System
Learning Objective
- Perform arithmetic calculations on metric units of length, mass, and volume.
Introduction
While knowing the different units used in the metric system is important, the real purpose behind learning the metric system is for you to be able to use these measurement units to calculate the size, mass, or volume of different objects. In practice, it is often necessary to convert one metric measurement to another unit. This happens frequently in the medical, scientific, and technical fields, where the metric system is commonly used.
If you have a prescription for `5,000` milligrams of medicine, and upon getting it filled, the dosage reads `5` grams of medicine, did the pharmacist make a mistake?
For a moment, imagine that you are a pharmacist. You receive three prescriptions for liquid amoxicillin: one calls for `2.5` centiliters, one calls for `0.3` deciliters, and one calls for `450` milliliters. Amoxicillin is stored in the refrigerator in `1` liter, `1` deciliter, and `1` centiliter containers. Which container should you use to ensure you are not wasting any of the unused drug?
To solve this problem, you need to know how to convert from one measurement to another as well as how to add different quantities together. Let’s take a look at how to do this.
Converting from Larger to Smaller Units
Converting between measurements in the metric system is simply a matter of identifying the unit that you have, the unit that you want to convert to, and then counting the number of units between them. A basic example of this is shown below.
|
Example
|
|
Problem
|
Convert `1` kilometer to decimeters.
|
|
|

|
Identify locations of kilometers and decimeters.
|
|
|
|
Kilometers (km) are larger than decimeters (dm), so you expect there to be more than one dm in a km.
|
|
|
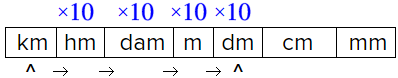
|
Count the intermediate units, multiplying by `10` as you go.
(Since you are going from a larger unit to a smaller unit, you multiply.)
|
|
|
`1" kilometer" * 10 * 10 * 10 * 10 = 10,000" decimeters"`
|
Multiply to find the number of decimeters in one kilometer.
|
|
Answer
|
`1" kilometer" = 10,000text( decimeters)`
|
|
This problem is straightforward because you are converting `1` kilometer to another unit. The example below shows how you would solve this problem if you were asked to convert `8.2` kilometers to decimeters. Notice that most steps are the same; the critical difference is that you multiply by `8.2` in the final step.
|
Example
|
|
Problem
|
Convert `8.2` kilometers to decimeters.
|
|
|
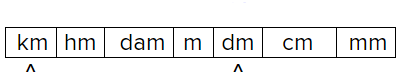
|
Identify locations of kilometers and decimeters.
|
|
|
|
Kilometers (km) are larger than decimeters (dm), so you expect there to be more than one dm in a km.
|
|
|

|
Count the intermediate units, multiplying by `10` as you go.
Since you are going from a larger unit to a smaller unit, multiply.
|
|
|
`8.2text( kilometers) * 10 * 10 * 10 * 10 = 82,000text( decimeters)`
|
Multiply to find the number of decimeters in `8.2` kilometers.
|
|
Answer
|
`8.2" kilometers" = 82,000text( decimeters)`
|
|
You can also apply the rules of base `10` to use the “move the decimal” shortcut method in this example. Notice how decimeters (dm) is four places to the right of kilometers (km); similarly, you move the decimal point four places to the right when converting `8.2` kilometers to decimeters.


|
Example
|
|
Problem
|
Convert `0.55` liters to centiliters.
|
|
|
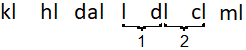
|
Count two places from liters to centiliters.
|
|
|
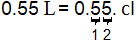
|
In `0.55` liters, move the decimal point two places to the right.
|
|
|
`0.55text( liters) = 55text( centiliters)`
|
|
|
Answer
|
`0.55" liters" = 55text( centiliters)`
|
|
|
How many dekaliters are in `0.5` deciliters?
A) `500`
B) `5`
C) `0.5`
D) `0.005`
A) `500`
Incorrect. A dekaliter is larger than a deciliter, so you would expect the number of dekaliters in `0.5` deciliters to be smaller than `0.5`. The correct answer is `0.005`.
B) `5`
Incorrect. A dekaliter is larger than a deciliter, so you would expect the number of dekaliters in `0.5` deciliters to be smaller than `0.5`. The correct answer is `0.005`.
C) `0.5`
Incorrect. Deciliters and dekaliters are different units of measurement, so you would not expect `0.5` deciliters to equal `0.5` dekaliters. The correct answer is `0.005`.
D) `0.005`
Correct. One deciliter is `100` times smaller than a dekaliter, so you move the decimal point two places to the left to convert `0.5` deciliters to `0.005` dekaliters.
|
Converting from Smaller to Larger Units
You can use similar processes when converting from smaller to larger units. When converting a larger unit to a smaller one, you multiply; when you convert a smaller unit to a larger one, you divide. Here is an example.
|
Example
|
|
Problem
|
Convert `739` centigrams to grams.
|
|
|

|
Identify locations of centigrams and grams.
|
|
|
|
Centigrams (cg) are smaller than grams (g), so you expect there to be less than `739` grams in `739` centigrams.
|
|
|

|
Count the intermediate units, dividing by `10` as you go.
Since you are going from a smaller unit to a larger unit, divide.
|
|
|
`739-:10-:10=7.39text( grams)`
|
Divide to find the number of grams in `739` centigrams.
|
|
Answer
|
`739" centigrams" = 7.39text( grams)`
|
|
Notice that the shortcut method of counting prefixes and moving the decimal the same number of places also works here. Just make sure you are moving the decimal point in the correct direction for the conversion.
|
Example
|
|
Problem
|
Convert `205.5` milliliters to kiloliters.
|
|
|

|
Count six places from milliliters to kiloliters.
|
|
|
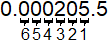
`205.5text( milliliters)=0.0002055text( kiloliters)`
|
Milliliters is smaller than kiloliters, so you expect the number `205.5` to get smaller as you move up the metric chart.
In `205.5` milliliters, move the decimal point six places to the left.
|
|
|
|
|
|
Answer
|
`205.5" milliliters" = 0.0002055text( kiloliters)`
|
|
Convert `3,085` milligrams to grams.
A) `3,085,000` grams
B) `308.5` grams
C) `3.085` grams
D) `0.3085` grams
A) `3,085,000` grams
Incorrect. Grams are larger than milligrams, so you would expect the number of grams in `3,085` milligrams to be less than `3,085`. The correct answer is `3.085` grams.
B) `308.5` grams
Incorrect. One gram is more than `10` times larger than a milligram, so you would expect the number of grams to be less than `308.5`. The correct answer is `3.085` grams.
C) `3.085` grams
Correct. One gram is `1,000` times larger than a milligram, so you can move the decimal point in `3,085` three places to the left.
D) `0.3085` grams
Incorrect. This is too small; one gram is `1,000`, not `10,000`, times larger than a milligram. The correct answer is `3.085` grams.
|
Factor Label Method
There is yet another method that you can use to convert metric measurements: the factor label methodOne method of converting a measurement from one unit of measurement to another unit of measurement. In this method, you multiply the original measurement by unit fractions containing different units of measurement to obtain the new unit of measurement.. You used this method when you were converting measurement units within the U.S. customary system.
The factor label method works the same in the metric system; it relies on the use of unit fractions and the cancelling of intermediate units. The table below shows some of the unit equivalentsStatements of equivalence between measurement units within a system or in comparison to another system of units. For example `1" foot" = 12` inches or `1" inch" = 2.54` centimeters are both examples of unit equivalents. and unit fractionsA fraction where the numerator and denominator are equal amounts. For example: `(1text( kg))/(1000text( g))` or `(12text( inches))/(1text( foot))`. Unit fractions serve to help with conversions in the Factor Label method. for length in the metric system. (You should notice that all of the unit fractions contain a factor of `10`. Remember that the metric system is based on the notion that each unit is `10` times larger than the one that came before it.)
Also, notice that two new prefixes have been added here: mega- (which is very big) and micro- (which is very small).
|
Unit Equivalents
|
Conversion Factors
|
|
`1" meter" = 1,000,000text( micrometers)`
|
`(1text( m))/(1,000,000mutext(m))`
|
`(1,000,000mutext(m))/(1text( m))`
|
|
`1" meter" = 1,000text( millimeters)`
|
`(1text( m))/(1,000text( mm)`
|
`(1,000text( mm))/(1text( m))`
|
|
`1" meter" = 100text( centimeters)`
|
`(1text( m))/(100text( cm))`
|
`(100text( cm))/(1text( m)`
|
|
`1" meter" = 10text( decimeters)`
|
`(1text( m))/(10text( dm))`
|
`(10text( dm))/(1text( m))`
|
|
`1" dekameter" = 10text( meters)`
|
`(1text( dam))/(10text( m))`
|
`(10text( m))/(1text( dam))`
|
|
`1" hectometer" = 100text( meters)`
|
`(1text( hm))/(100text( m))`
|
`(100text( m))/(1text( hm))`
|
|
`1" kilometer" = 1,000text( meters)`
|
`(1text( km))/(1,000text( m))`
|
`(1,000text( m))/(1text( km))`
|
|
`1" megameter" = 1,000,000text( meters)`
|
`(1text( Mm))/(1,000,000text( m))`
|
`(1,000,000text( m))/(1text( Mm))`
|
When applying the factor label method in the metric system, be sure to check that you are not skipping over any intermediate units of measurement!
|
Example
|
|
Problem
|
Convert `7,225` centimeters to meters.
|
|
|
`7,225text( centimeters)=text(? meters)`
|
Meters is larger than centimeters, so you expect your answer to be less than `7,225`.
|
|
|
`(7,225text( centimeters))/1*(1text( meter))/(100text( centimeters))=text(? meters)`
|
Using the factor label method, write `7,225` centimeters as a fraction and use unit fractions to convert it to meters.
|
|
|
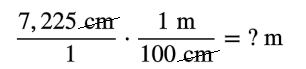
`(7,225)/1*(1text( meter))/100=(7,225text( meters))/100`
`(7,225text( meters))/100=72.25text( meters)`
|
Cancel similar units, multiply, and simplify.
|
|
Answer
|
`7,225text( centimeters)=72.25text( meters)`
|
|
Using whichever method you prefer, convert `32.5` kilometers to meters.
A) `32,500text( meters)`
B) `325text( meters)`
C) `0.325text( meters)`
D) `0.00325text( meters)`
A) `32,500text( meters)`
Correct. To find the number of meters in `32.5` kilometers, you can set up the following equation: `(32.5text( kilometers))/1*(1,000text( meters))/(1text( kilometer))=(32,500text( meters))/1.` The kilometers units cancel, leaving the answer in meters.
B) `325text( meters)`
Incorrect. A kilometer is more than `10` times the size of a meter; look at the unit fractions and try your calculations again. The correct answer is `32,500` meters.
C) `0.325text( meters)`
Incorrect. A kilometer is larger than a meter, so you would expect the number of meters in `32.5` kilometers to be more than `32.5`. Look at the unit fractions and try your calculations again. The correct answer is `32,500` meters.
D) `0.00325text ( meters)`
Incorrect. A kilometer is larger than a meter, so you would expect the number of meters in `32.5` kilometers to be more than `32.5`. Look at the unit fractions and try your calculations again. The correct answer is `32,500` meters.
|
Now that you have seen how to convert among metric measurements in multiple ways, let’s revisit the problem posed earlier.
|
Example
|
|
Problem
|
If you have a prescription for `5,000` milligrams of medicine, and upon getting it filled, the dosage reads `5` grams of medicine, did the pharmacist make a mistake?
|
|
|
`5,000text( milligrams)=text(? grams)`
|
Need to convert milligrams to grams.
|
|
|
`(5,000text( milligrams))/1*(1text( gram))/(1,000text( milligrams))=text(? grams)`

`(5,000*1text( gram))/(1*1,000)=(5,000text( grams))/(1,000)`
`(5,000text( grams))/(1,000)=5text( grams)`
|
|
|
Answer
|
`5text( grams) = 5,000text( milligrams)`, so the pharmacist did not make a mistake.
|
Summary
To convert among units in the metric system, identify the unit that you have, the unit that you want to convert to, and then count the number of units between them. If you are going from a larger unit to a smaller unit, you multiply by `10` successively. If you are going from a smaller unit to a larger unit, you divide by `10` successively. The factor label method can also be applied to conversions within the metric system. To use the factor label method, you multiply the original measurement by unit fractions; this allows you to represent the original measurement in a different measurement unit.