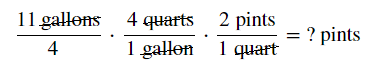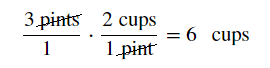Capacity
Learning Objectives
- Define units of capacity and convert from one to another.
- Perform arithmetic calculations on units of capacity.
- Solve application problems involving units of capacity.
Introduction
Capacity The amount of liquid (or other pourable substance) that an object can hold when it's full.is the amount of liquid (or other pourable substance) that an object can hold when it’s full. When a liquid, such as milk, is being described in gallons or quarts, this is a measure of capacity.
Understanding units of capacity can help you solve problems like this: Sven and Johanna were hosting a potluck dinner. They did not ask their guests to tell them what they would be bringing, and three people ended up bringing soup. Erin brought `1` quart, Richard brought `3` pints, and LeVar brought `9` cups. How many cups of soup did they have all together?
There are five main units for measuring capacity in the U.S. customary measurement system. The smallest unit of measurement is a fluid ounceA unit of capacity equal to `1/8` of a cup. One fluid ounce of water at `62`°F weighs about one ounce. . “Ounce” is also used as a measure of weight, so it is important to use the word “fluid” with ounce when you are talking about capacity. Sometimes the prefix “fluid” is not used when it is clear from the context that the measurement is capacity, not weight.
The other units of capacity in the customary system are the cupA unit of capacity equal to `8` fluid ounces., pintA unit of capacity equal to `16` fluid ounces, or `2` cups., quartA unit of capacity equal to `32` fluid ounces, or `4` cups., and gallonA unit equal to `4` quarts, or `128` fluid ounces.. The table below describes each unit of capacity and provides an example to illustrate the size of the unit of measurement.
|
Fluid Ounce
A unit of capacity equal to `1/8` of a cup. One fluid ounce of water at `62^@` Fahrenheit weighs about one ounce. The amount of liquid medicine is often measured in fluid ounces.
|
|
|
Cup
A unit equal to `8` fluid ounces. The capacity of a standard measuring cup is one cup.
|

|
|
Pint
A unit equal to `16` fluid ounces, or `2` cups. The capacity of a carton of ice cream is often measured in pints.
|

|
|
Quart
A unit equal to `32` fluid ounces, or `4` cups. You often see quarts of milk being sold in the supermarket.
|

|
|
Gallon
A unit equal to `4` quarts, or `128` fluid ounces. When you fill up your car with gasoline, the price of gas is often listed in dollars per gallon.
|

|
You can use any of these five measurement units to describe the capacity of an object, but it makes more sense to use certain units for certain purposes. For example, it makes more sense to describe the capacity of a swimming pool in gallons and the capacity of an expensive perfume in fluid ounces.
Sometimes you will need to convert between units of measurement. For example, you might want to express `5` gallons of lemonade in cups if you are trying to determine how many `8`-fluid ounce servings the amount of lemonade would yield.
The table below shows some of the most common equivalents and conversion factors for the five customary units of measurement of capacity.
|
Unit Equivalents
|
Conversion Factors (heavier to lighter units of measurement)
|
Conversion Factors (lighter to heavier units of measurement)
|
|
`1text( cup) = 8text( fluid ounces)`
|
`(1text( cup))/(8text( fluid ounces)`
|
`(8text( fluid ounces))/(1text( cup))`
|
|
`1text( pint) = 2text( cups)`
|
`(1text( pint))/(2text( cups))`
|
`(2text( cups))/(1text( pint))`
|
|
`1text( quart) = 2text( pints)`
|
`(1text( quart))/(2text( pints))`
|
`(2text( pints))/(1text( quart))`
|
|
`1text( quart) = 4text( cups)`
|
`(1text( quart))/(4text( cups))`
|
`(4text( cups))/(1text( quart))`
|
|
`1text( gallon) = 4text( quarts)`
|
`(1text( gallon))/(4text( quarts))`
|
`(4text( quarts))/(1text( gallon))`
|
|
`1text( gallon) = 16text( cups)`
|
`(1text( gallon))/(16text( cups))`
|
`(16text( cups))/(1text( gallon))`
|
Converting Between Units of Capacity
As with converting units of length and weight, you can use the factor label method to convert from one unit of capacity to another. An example of this method is shown below.
|
Example
|
|
Problem
|
How many pints is `2 3/4` gallons?
|
|
|
`2 3/4text( gallons)=text(? pints)`
|
Begin by reasoning about your answer. Since a gallon is larger than a pint, expect the answer in pints to be a number greater than `2 3/4`.
|
|
|
`(11text( gallons))/4*(4text( quarts))/(1text( gallon))*(2text( pints))/(1text( quart))=text(? pints`
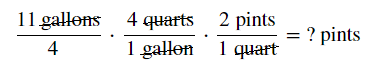
|
The table above does not contain a conversion factor for gallons and pints, so you cannot convert it in one step. However, you can use quarts as an intermediate unit, as shown here.
Set up the equation so that two sets of labels cancel: gallons and quarts.
|
|
|
`11/4*4/1*(2text( pints))/1=text(? pints)`
`(11*4* 2text( pints))/(4*1*1)=text(? pints`
`(88text( pints))/4=22text( pints)`
|
Multiply and simplify.
|
|
Answer
|
`2 3/4` gallons is `22` pints.
|
|
|
Example
|
|
Problem
|
How many gallons is `32` fluid ounces?
|
|
|
`32text( fluid ounces)=text(? gallons)`
|
Begin by reasoning about your answer. Since gallons is a larger unit than fluid ounces, expect the answer to be less than `32`.
|
|
|
`(32text( fl oz))/1*(1text( cup))/(8text( fl oz))*(1text( pint))/(2text( cups))*(1text( quart))/(2text( pints))*(1text( gallon))/(4text( quarts))=text(? gallons)`
|
The table above does not contain a conversion factor for gallons and fluid ounces, so you cannot convert it in one step. Use a series of intermediate units, as shown here.
|
|
|

`32/1*1/8*1/2*1/2*(1text( gallon))/4=text(? gallons)`
|
Cancel units that appear in both the numerator and denominator.
Multiply and simplify.
|
|
|
`(32*1*1*1*1text( gallon))/(1*8*2*2*4)=text(? gallons)`
`(32text( gallons))/128=1/4text( gallon)`
|
|
|
Answer
|
`32` fluid ounces is the same as `1/4` gallon.
|
|
|
Find the sum of `4` gallons and `2` pints. Express your answer in cups.
A) `68` cups
B) `6` cups
C) `2` gallons and `4` pints
D) `34` pints
A) `68` cups
Correct. Each gallon has `16` cups, so `4 * 16 = 64` will give you the number of cups in `4` gallons. Each pint has `2` cups, so `2 * 2 = 4` will give you the number of cups in `2` pints. `64 + 4 = 68` cups.
B) `6` cups
Incorrect. You cannot add measurements expressed in different units. First convert each amount to cups and then add. The correct answer is `68` cups.
C) `2` gallons and `4` pints
Incorrect. This is not the correct amount. First convert each amount to cups and then add them together. Also, notice that this answer is not expressed in cups, as the problem requires. The correct answer is `68` cups.
D) `34` pints
Incorrect. This is the correct amount, but it is expressed in the incorrect unit: pints. Multiply `34` pints by `2` (since there are `2` cups in a pint) to give the amount in cups as required. The correct answer is `68` cups.
|
Applying Unit Conversions
There are times when you will need to combine measurements that are given in different units. In order to do this, you need to convert first so that the units are the same.
Consider the situation posed earlier in this topic.
|
Example
|
|
Problem
|
Sven and Johanna were hosting a potluck dinner. They did not ask their guests to tell them what they would be bringing, and three people ended up bringing soup. Erin brought `1` quart, Richard brought `3` pints, and LeVar brought `9` cups. How much soup did they have total?
|
|
|
`1" quart" + 3" pints" + 9" cups"`
`1text( quart) = 4text( cups)`
|
Since the problem asks for the total amount of soup, you must add the three quantities. Before adding, you must convert the quantities to the same unit.
The problem does not require a particular unit, so you can choose. Cups might be the easiest computation.
|
|
|
|
This is given in the table of equivalents.
|
|
|
`(3text( pints))/1*(2text( cups))/(1text( pint))=text( ? cups)`
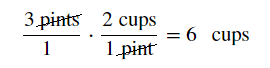
|
Use the factor label method to convert pints to cups.
|
|
|
`4text( cups)+6text( cups)+9text( cups)=19text( cups)`
|
Add the `3` quantities.
|
|
Answer
|
There are `19` cups of soup for the dinner.
|
|
Example
|
|
Problem
|
Natasha is making lemonade to bring to the beach. She has two containers. One holds one gallon and the other holds `2` quarts. If she fills both containers, how many cups of lemonade will she have?
|
|
|
`1text( gallon)+2text( quarts)=text(? cups)`
|
This problem requires you to find the sum of the capacity of each container and then convert that sum to cups.
|
|
|
`4text( quarts)+2text( quarts)=6text( quarts)`
|
First, find the sum in quarts. `1` gallon is equal to `4` quarts.
|
|
|
`(6text( quarts))/1*(2text( pints))/(1text( quart))*(2text( cups))/(1text( pint))=text(? cups)`

`6 * 2 * 2 = 24` cups
|
Since the problem asks for the capacity in cups, convert `6` quarts to cups.
Cancel units that appear in both the numerator and denominator.
Multiply.
|
|
Answer
|
Natasha will have `24` cups of lemonade.
|
|
Another way to work the problem above would be to first change `1` gallon to `16` cups and change `2` quarts to `8` cups. Then add: `16 + 8 = 24` cups.
|
Alan is making chili. He is using a recipe that makes `24` cups of chili. He has a `5`-quart pot and a `2`-gallon pot and is trying to determine whether the chili will all fit in one of these pots. Which of the pots will fit the chili?
A) The chili will not fit into either of the pots.
B) The chili can fit into either pot.
C) The chili will fit into the `5`-quart pot only.
D) The chili will fit into the `2`-gallon pot only.
A) The chili will not fit into either of the pots.
Incorrect. The `5`-quart pot will hold only `20` cups, leaving `4` cups that won’t fit into the pot. However, the `2`-gallon pot is large enough to fit the chili. The correct answer is the `2`-gallon pot only.
B) The chili can fit into either pot.
Incorrect. The `5`-quart pot will hold only `20` cups, so the `24` cups of chili cannot fit in there. The correct answer is the `2`-gallon pot only.
C) The chili will fit into the `5`-quart pot only.
Incorrect. The `5`-quart pot will hold only `20` cups. The `2`-gallon pot will hold `32` cups. The correct answer is the `2`-gallon pot only.
D) The chili will fit into the `2`-gallon pot only.
Correct. `5text( quarts) = 5*4text( cups)=20text( cups)`, so `24` cups of chili will not fit into the `5`-quart pot. `2text( gallons) = 32text( cups)`, so `24` cups of chili will fit in this pot.
|
Summary
There are five basic units for measuring capacity in the U.S. customary measurement system. These are the fluid ounce, cup, pint, quart, and gallon. These measurement units are related to one another, and capacity can be described using any of the units. Typically, people use gallons to describe larger quantities and fluid ounces, cups, pints, or quarts to describe smaller quantities. Often, in order to compare or to solve problems involving the amount of liquid in a container, you need to convert from one unit of measurement to another.