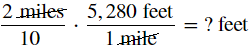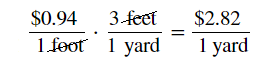Length

MeasurementThe use of standard units to find out the size or quantity of items such as length, width, height, mass, weight, volume, temperature or time. is a number that describes the size or amount of something. You can measure many things like length, area, capacity, weight, temperature and time. In the United States, two main systems of measurement are used: the metric systemA widely used system of measurement that is based on the decimal system and multiples of `10`. and the U.S. customary measurement systemThe most common system of measurement used in the United States. It is based on English measurement systems of the 18th century.. This topic addresses the measurement of length using the U.S. customary measurement system.

Suppose you want to purchase tubing for a project, and you see two signs in a hardware store: `$1.88` for `2` feet of tubing and `$5.49` for `3` yards of tubing. If both types of tubing will work equally well for your project, which is the better price? You need to know about two units of measurementA standard amount or quantity. For example, an inch is a unit of measurement., yards and feet, in order to determine the answer.

LengthThe distance from one end to the other or the distance from one point to another. is the distance from one end of an object to the other end, or from one object to another. For example, the length of a letter-sized piece of paper is `11` inches. The system for measuring length in the United States is based on the four customary units of length: inchA unit for measuring length in the U.S. customary measurement system. `1" foot" = 12` inches, footA unit for measuring length in the U.S. customary measurement system. `1" foot" = 12` inches, yardA unit for measuring length in the U.S. customary measurement system. `1" yard" = 3` feet or `36` inches., and mileA unit for measuring length in the U.S. customary measurement system. `1" mile" = 5,280` feet or `1,760` yards.. Below are examples to show measurement in each of these units.

Unit	Description	Image
Inch/Inches	Some people donate their hair to be made into wigs for cancer patients who have lost hair as a result of treatment. One company requires hair donations to be at least `8` inches long.
	Frame size of a bike: the distance from the center of the crank to the top of the seat tube. Frame size is usually measured in inches. This frame is `16` inches.
Foot/Feet	Rugs are typically sold in standard lengths. One typical size is a rug that is `8` feet wide and `11` feet long. This is often described as an `8` by `11` rug.
Yard/Yards	Soccer fields vary some in their size. An official field can be any length between `100` and `130` yards.
Mile/Miles	A marathon is `26.2` miles long. One marathon route is shown in the map to the right.

You can use any of these four U.S. customary measurement units to describe the length of something, but it makes more sense to use certain units for certain purposes. For example, it makes more sense to describe the length of a rug in feet rather than miles, and to describe a marathon in miles rather than inches.

You may need to convert between units of measurement. For example, you might want to express your height using feet and inches (`5` feet `4` inches) or using only inches (`64` inches). You need to know the unit equivalents in order to make these conversions between units.

The table below shows equivalents and conversion factors for the four customary units of measurement of length.

Unit Equivalents	Conversion Factors (longer to shorter units of measurement)	Conversion Factors (shorter to longer units of measurement)
`1" foot" = 12 " inches"`	`(12text( inches))/(1text( foot)`	`(1text( foot))/(12text( inches))`
`1" yard" = 3 " feet"`	`(3text( feet))/(1text( yard))`	`(1text( yard))/(3text( feet))`
`1" mile" = 5,280 " feet"`	`(5,280text( feet))/(1text( mile))`	`(1text( mile))/(5,280text( feet))`

Note that each of these conversion factors is a ratio of equal values, so each conversion factor equals `1`. Multiplying a measurement by a conversion factor does not change the size of the measurement at all since it is the same as multiplying by `1`; it just changes the units that you are using to measure.

You can use the conversion factors to convert a measurement, such as feet, to another type of measurement, such as inches.

Note that there are many more inches for a measurement than there are feet for the same measurement, as feet is a longer unit of measurement. You could use the conversion factor `(12text( inches))/(1text( foot)`.

If a length is measured in feet, and you’d like to convert the length to yards, you can think, “I am converting from a shorter unit to a longer one, so the length in yards will be less than the length in feet.” You could use the conversion factor `(1text( yard))/(3text( feet))`.

If a distance is measured in miles, and you want to know how many feet it is, you can think, “I am converting from a longer unit of measurement to a shorter one, so the number of feet would be greater than the number of miles.” You could use the conversion factor `(5,280text( feet))/(1text( mile))` .

You can use the factor label methodOne method of converting a measurement from one unit of measurement to another unit of measurement. In this method, you multiply the original measurement by unit fractions containing different units of measurement to obtain the new unit of measurement. to convert a length from one unit of measure to another using the conversion factors. In the factor label method, you multiply by unit fractions to convert a measurement from one unit to another. Study the example below to see how the factor label method can be used to convert `3 1/2` feet into an equivalent number of inches.

Example
Problem	How many inches are in `3 1/2` feet?
	`3 1/2text( feet)=text(?)text( inches)`	Begin by reasoning about your answer. Since a foot is longer than an inch, this means the answer would be greater than `3 1/2`.
	`3 1/2text( feet)*(12text( inches))/(1text( foot))=text(? inches)`	Find the conversion factor that compares inches and feet, with “inches” in the numerator, and multiply.
	`(7text( feet))/2*(12text( inches))/(1text( foot))=text(? inches)`	Rewrite the mixed number as an improper fraction before multiplying.
	`7/2*(12text( inches))/1=text(? inches)`	You can cancel similar units when they appear in the numerator and the denominator. So here, cancel the similar units “feet” and “foot.” This eliminates this unit from the problem.
	`(712text( inches))/(21)=text(? inches)`	Rewrite as multiplication of numerators and denominators.
	`(84text( inches))/(2)=text(? inches)`	Multiply.
	`(84text( inches))/2= 42text( inches)`	Divide.
Answer	There are `42` inches in `3 1/2` feet.

Notice that by using the factor label method you can cancel the units out of the problem, just as if they were numbers. You can only cancel if the unit being cancelled is in both the numerator and denominator of the fractions you are multiplying.

In the problem above, you cancelled feet and foot leaving you with inches, which is what you were trying to find.

You could not cancel the feet because the unit is not the same in both the numerator and the denominator. So if you complete the computation, you would still have both feet and inches in the answer and no conversion would take place.

Example
Problem	How many yards is `7` feet?
	`7text( feet)=text(? yards)`	Start by reasoning about the size of your answer. Since a yard is longer than a foot, there will be fewer yards. So your answer will be less than `7`.
	`7text( feet)*(1text( yard))/(3text( feet))=text(? yards)`	Find the conversion factor that compares feet and yards, with yards in the numerator.
	`(7text( feet))/1*(1text( yard))/(3text( feet))=text(? yards)`	Rewrite the whole number as a fraction in order to multiply.
	`7/1*(1text( yard))/3=text(? yards)`	Cancel the similar units “feet” and “feet” leaving only yards.
	`(71text( yard))/(13)=text(? yards)`	Multiply.
	`(7text( yards))/3=2 1/3text( yards)`	Divide, and write as a mixed number.
Answer	`7` feet equals `2 1/3` yards.

Note that if the units do not cancel to give you the answer you are trying to find, you may not have used the correct conversion factor.

There are times when you will need to perform computations on measurements that are given in different units. For example, consider the tubing problem given earlier. You must decide which of the two options is a better price, and you have to compare prices given in different unit measurements.

In order to compare, you need to convert the measurements into one single, common unit of measurement. To be sure you have made the computation accurately, think about whether the unit you are converting to is smaller or larger than the number you have. Its relative size will tell you whether the number you are trying to find is greater or lesser than the given number.

Example
Problem	An interior decorator needs border trim for a home she is wallpapering. She needs `15` feet of border trim for the living room, `30` feet of border trim for the bedroom, and `26` feet of border trim for the dining room. How many yards of border trim does she need?
	`15" feet" + 30" feet" + 26" feet" = 71" feet" `	You need to find the total length of border trim that is needed for all three rooms in the house. Since the measurements for each room are given in feet, you can add the numbers.
	`71text( feet)=text(? yards)`	How many yards is `71` feet? Reason about the size of your answer. Since a yard is longer than a foot, there will be fewer yards. Expect your answer to be less than `71`.
	`(71text( feet))/1*(1text( yard))/(3text( feet))=text(? yards)`	Use the conversion factor `(1text( yard))/(3text( feet))`.
	`71/1*(1text( yard))/3=text(? yards)`	Since “feet” is in the numerator and denominator, you can cancel this unit.
	`(711text( yard))/(13)=text(? yards)` `(71text( yards))/3=text(? yards)`	Multiply.
	`(71text( yards))/3=23 2/3text( yards)`	Divide, and write as a mixed number.
Answer	The interior decorator needs `23 2/3` yards of border trim.

The next example uses the factor label method to solve a problem that requires converting from miles to feet.

Example
Problem	Two runners were comparing how much they had trained earlier that day. Jo said, “According to my pedometer, I ran `8.3` miles.” Alex said, “That’s a little more than what I ran. I ran `8.1` miles.” How many more feet did Jo run than Alex?
	`8.3` miles `-text( )8.1` miles `= 0.2` `0.2text( mile)=2/10text( mile)`	You need to find the difference between the distance Jo ran and the distance Alex ran. Since both distances are given in the same unit, you can subtract and keep the unit the same.
	`2/10text( mile)=text(? feet)`	Since the problem asks for the difference in feet, you must convert from miles to feet. How many feet is `0.2` miles? Reason about the size of your answer. Since a mile is longer than a foot, the distance when expressed as feet will be a number greater than `0.2`.
	`(2text( miles))/10*(5,280text( feet))/(1text( mile))=text(? feet)`	Use the conversion factor `(5,280text( feet))/(1text( mile))`.
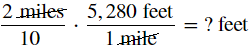
	$The image shows a unit fraction 2 miles over 10, times, 5,280 feet over 1 mile, equals, question mark feet. The units, miles and mile, are crossed out.$ `2/10*(5,280text( feet))/1=text(? feet)`	Since “mile” is in the numerator and denominator, you can cancel this unit.
	`(25,280text( feet))/(101)=text(? feet)`	Multiply.
	`(10,560text( feet))/10=text(? feet)` `(10,560text( feet))/10=1,056text( feet)`	Divide.
Answer	Jo ran `1,056` feet farther than Alex.

Example
Problem	You are walking through a hardware store and notice two sales on tubing. `3` yards of Tubing A costs `$5.49`. Tubing B sells for `$1.88` for `2` feet. Either tubing is acceptable for your project. Which tubing is less expensive?
	Tubing A `3" yards" = $5.49`	Find the unit price for each tubing. This will make it easier to compare.
	`($5.49 -: 3)/(3 " yards "-:3)=($1.83)/(1" yard"`	Find the cost per yard of Tubing A by dividing the cost of `3` yards of the tubing by `3`.
	Tubing B `2text( feet) = $1.88` `($1.88 -: 2)/(2" feet "-:2)=($0.94)/(1text( foot))`	Tubing B is sold by the foot. Find the cost per foot by dividing `$1.88` by `2` feet.
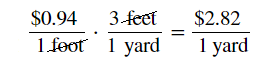
	`($0.94)/(1text( foot))*(3text( feet))/(1text( yard))=($?)/text(? yard)` `$2.82` per yard	To compare the prices, you need to have the same unit of measure. Use the conversion factor `(3text( feet))/(1text( yard)`, cancel and multiply.
	Tubing A: `$1.83` per yard Tubing B: `$2.82` per yard	Compare prices for `1` yard of each tubing.
Answer	Tubing A is less expensive than Tubing B.

In the problem above, you could also have found the price per foot for each kind of tubing and compared the unit prices of each per foot.

The four basic units of measurement that are used in the U.S. customary measurement system are: inch, foot, yard, and mile. Typically, people use yards, miles, and sometimes feet to describe long distances. Measurement in inches is common for shorter objects or lengths.

You need to convert from one unit of measure to another if you are solving problems that include measurements involving more than one type of measurement. Each of the units can be converted to one of the other units using the table of equivalents, the conversion factors, and/or the factor label method shown in this topic.

Learning Objectives

Introduction

Units of Length

Converting Between Units of Length

Applying Unit Conversions

Summary