Convert Percents, Decimals, and Fractions

Three common formats for numbers are fractions, decimals, and percents. Percents are often used to communicate a relative amount. You have probably seen them used for discounts, where the percent of discount can apply to different prices. Percents are also used when discussing taxes and interest rates on savings and loans.

A percentA ratio that compares a number to `100`. “Per cent” means “per `100`,” or “how many out of `100`.” is a ratio of a number to `100`. Per cent means “per `100`,” or “how many out of `100`.” You use the symbol % after a number to indicate percent.

Notice that `12` of the `100` squares in the grid below have been shaded green. This represents `12` percent (`12` per `100`).

How many of the squares in the grid above are unshaded? Since `12` are shaded and there are a total of `100` squares, `88` are unshaded. The unshaded portion of the whole grid is `88` parts out of `100`, or `88%` of the grid. Notice that the shaded and unshaded portions together make `100%` of the grid (`100` out of `100` squares).

Example
Problem	What percent of the grid is shaded?
	The grid is divided into `100` smaller squares, with `10` squares in each row.
	`23` squares out of `100` squares are shaded.
Answer	`23%` of the grid is shaded.

Example
Problem	What percent of the large square is shaded?
	The grid is divided into `10` rectangles. For percents, you need to look at `100` equal-sized parts of the whole. You can divide each of the `10` rectangles into `10` pieces, giving `100` parts.
	`30` small squares out of `100` squares are shaded.
Answer	`30%` of the large square is shaded.

It is often helpful to change the format of a number. For example, you may find it easier to add decimals than to add fractions. If you can write the fractions as decimals, you can add them as decimals. Then you can rewrite your decimal sum as a fraction, if necessary.

Example
Problem	Write `25%` as a simplified fraction and as a decimal.
Write as a fraction.	`25%=25/100`	Since `%` means "out of `100`," `25%` means `25` out of `100`. You write this as a fraction, using `100` as the denominator.
	`25/100=(25-:25)/(100-:25)=1/4`	Simplify the fraction by dividing the numerator and denominator by the common factor `25.`
Write as a decimal.	`25%=25/100=0.25`	You can also just move the decimal point in the whole number `25` two places to the left to get `0.25`.
Answer	`25%=1/4=0.25`

Notice in the diagram below that `25%` of a grid is also `1/4` of the grid, as you found in the example.

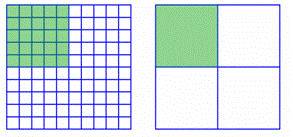
Notice that in the previous example, rewriting a percent as a decimal takes just a shift of the decimal point. You can use fractions to understand why this is the case. Any percentage `x` can be represented as the fraction `x/100` , and any fraction `x/100` can be written as a decimal by moving the decimal point in `x` two places to the left. For example, `81%` can be written as `81/100`, and dividing `81` by `100` results in `0.81`. People often skip over the intermediary fraction step and just convert a percent to a decimal by moving the decimal point two places to the left.

In the same way, rewriting a decimal as a percent (or as a fraction) requires few steps.

Example
Problem	Write `0.6` as a percent and as a simplified fraction.
Write as a percent.	`0.6 = 0.60 = 60%`	Write `0.6` as `0.60`, which is `60` hundredths. `60` hundredths is `60` percent. You can also move the decimal point two places to the right to find the percent equivalent.
Write as a fraction.	`0.6=6/10`	To write `0.6` as a fraction, you read the decimal, `6` tenths, and write `6` tenths in fraction form.
	`6/10=(6-:2)/(10-:2)=3/5`	Simplify the fraction by dividing the numerator and denominator by `2`, a common factor.
Answer	`0.6=60%=3/5`

In this example, the percent is not a whole number. You can handle this in the same way, but it’s usually easier to convert the percent to a decimal and then convert the decimal to a fraction.

Example
Problem		Write `5.6%` as a decimal and as a simplified fraction.
Write as a decimal.		`5.6% = 0.056`	Move the decimal point two places to the left. In this case, insert a `0` in front of the `5` `(05.6)` in order to be able to move the decimal to the left two places.
Write as a fraction.		`0.056=56/(1,000)`	Write the fraction as you would read the decimal. The last digit is in the thousandths place, so the denominator is `1,000`.
		`56/(1,000)=(56-:8)/(1,000-:8)=7/125`	Simplify the fraction by dividing the numerator and denominator by `8,` a common factor.
Answer	`5.6%=7/125=0.056`

In order to write a fraction as a decimal or a percent, you can write the fraction as an equivalent fraction with a denominator of `10` (or any other power of `10` such as `100` or `1,000`), which can be then converted to a decimal and then a percent.

Example
Problem	Write `3/4` as a decimal and as a percent.
Write as a decimal.	`3/4=(325)/(425)=75/100`	Find an equivalent fraction with `10`, `100`, `1,000`, or other power of `10` in the denominator. Since `100` is a multiple of `4`, you can multiply `4` by `25` to get `100`. Multiply both the numerator and the denominator by `25`.
	`75/100=0.75`	Write the fraction as a decimal with the `5` in the hundredths place.
Write as a percent.	`0.75 = 75%`	To write the decimal as a percent, move the decimal point two places to the right.
Answer	`3/4=0.75=75%`

If it is difficult to find an equivalent fraction with a denominator of `10`, `100`, `1,000`, and so on, you can always divide the numerator by the denominator to find the decimal equivalent.

Example
Problem	Write `3/8` as a decimal and as a percent.
Write as a decimal.	`3/8=3-:8`	Divide the numerator by the denominator. `3-:8=0.375`
Write as a percent.	`0.375 = 37.5%`	To write the decimal as a percent, move the decimal point two places to the right.
Answer	`3/8=0.375=37.5%`

All the previous examples involve fractions and decimals less than `1`, so all of the percents you have seen so far have been less than `100%`.

Percents greater than `100%` are possible as well. Percents more than `100%` are used to describe situations where there is more than one whole (fractions and decimals greater than `1` are used for the same reason).

In the diagram below, `115%` is shaded. Each grid is considered a whole, and you need two grids for `115%`.

Expressed as a decimal, the percent `115%` is `1.15`; as a fraction, it is `1 15/100`, or `1 3/20`. Notice that you can still convert among percents, fractions, and decimals when the quantity is greater than one whole.

Numbers greater than one that include a fractional part can be written as the sum of a whole number and the fractional part. For instance, the mixed number `3 1/4` is the sum of the whole number `3` and the fraction `1/4*3 1/4=3+1/4`.

Example
Problem	Write `2 7/8` as a decimal and as a percent.
	`2 7/8=2+7/8`	Write the mixed fraction as `2` wholes plus the fractional part.
Write as a decimal.	`7/8=7-:8`	Write the fractional part as a decimal by dividing the numerator by the denominator `7-:8=0.875`.
	`2+0.875=2.875`	Add `2` to the decimal.
Write as a percent.	`2.875 = 287.5%`	Now you can move the decimal point two places to the right to write the decimal as a percent.
Answer	`2 7/8=2.875=287.5%`

Note that a whole number can be written as a percent. `100%` means one whole; so two wholes would be `200%`.

Example
Problem	Write `375%` as a decimal and as a simplified fraction.
Write as a decimal.	`375% = 3.75`	Move the decimal point two places to the left. Note that there is a whole number along with the decimal as the percent is more than `100%`.
Write as a fraction.	`3.75 = 3 + 0.75`	Write the decimal as a sum of the whole number and the fractional part.
	`0.75=75/100`	Write the decimal part as a fraction.
	`75/100=(75-:25)/(100-:25)=3/4`	Simplify the fraction by dividing the numerator and denominator by a common factor of `25`.
	`3+3/4=3 3/4`	Add the whole number part to the fraction.
Answer	`375%=3.75=3 3/4`

Percents are a common way to represent fractional amounts, just as decimals and fractions are. Any number that can be written as a decimal, fraction, or percent can also be written using the other two representations.

Learning Objectives

Introduction

The Meaning of Percent

Rewriting Percents, Decimals, and Fractions

Mixed Numbers

Summary