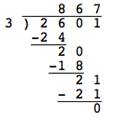
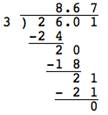
Multiplying and Dividing Decimals

Learning Objectives

Introduction

As with whole numbers, sometimes you run into situations where you need to multiply or divide decimals. And just as there is a correct way to multiply and divide whole numbers, so, too, there is a correct way to multiply and divide decimals.

Imagine that a couple eats dinner at a Japanese steakhouse. The bill for the meal is `$58.32`—which includes a tax of `$4.64`. To calculate the tip, they can double the tax. So if they know how to multiply `$4.64` by `2`, the couple can figure out how much they should leave for the tip.

Here’s another problem. Andy just sold his van that averaged `20` miles per gallon of gasoline. He bought a new pickup truck and took it on a trip of `614.25` miles. He used `31.5` gallons of gas to make it that far. Did Andy get better gas mileage with the new truck?

Both of these problems can be solved by multiplying or dividing decimals. Here’s how to do it.

Multiplying Decimals

Multiplying decimals is the same as multiplying whole numbers except for the placement of the decimal point in the answer. When you multiply decimals, the decimal point is placed in the product The result when two numbers are multiplied. For example, the product of `4 * 5` is `20`. so that the number of decimal places in the product is the sum of the decimal places in the factors A number that is multiplied by another number or numbers to get a product. For example, in the equation `4 * 5 = 20`, `4` and `5` are factors. .

Let’s compare two multiplication problems that look similar: `214 * 36`, and `21.4 * 3.6`.

Notice how the digits in the two solutions are exactly the same: `7`, `7`, `0`, and `4`. The multiplication does not change at all. The difference lies in the placement of the decimal point in the final answers: `214 * 36 = 7,704`, and `21.4 * 3.6 = 77.04`.

To find out where to put the decimal point in a decimal multiplication problem, count the total number of decimal places in each of the factors.

`21.4` the first factor has one decimal place

`3.6` the second factor has one decimal place

`77.04` the product will have `1 + 1 = 2` decimal places

Note that the decimal points do not have to be aligned as for addition and subtraction.

Example

Problem

`3.04*6.1=?` 

 

 

 

 

Set up the problem.

 

Multiply `3.04` by `6.1`.

 

Add `304` and `18240`.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Count the total number of decimal places in the factors and insert the decimal point in the product.

 

`2` decimal places in `3.04`.

`1` decimal place in `6.1`.

 

`3` total decimal places.

Answer

`3.04 * 6.1 = 18.544`

Sometimes you may need to insert zeros in front of the product so that you have the right number of decimal places. See the final answer in the example below:

Example

Problem

`0.037*0.08=?` 

 

 

 

 

 

 

 

Set up the problem.

 

Multiply `0.037` by `0.08`.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Count the total number of decimal places in the factors and insert the decimal point in the product.

 

`3` decimal places in `0.037`.

`2` decimal places in `0.08`.

`5` decimal places in the product.

Answer

`0.037 * 0.08 = 0.00296`

Note that you needed to add zeros before `296` to get the `5` decimal places.

If one or more zeros occur on the right in the product, they are not dropped until after the decimal point is inserted.

Example

Problem

`2.04*1.95=?` 

 

 

 

 

 

 

 

 

 

Set up the problem.

 

Multiply `2.04` by `1.95`.

 

 

Add `1020, 18360, "and"\ 20400`.

 

 

 

 

 

 

 

 

 

 

`2` decimal places in `2.04`.

`2` decimal places `1.95`.

 

 

 

`4` decimal places.

 

 

Answer

`2.04 * 1.95 = 3.978`

Answer can omit the final trailing `0`.

 

Multiplying Decimals

 

To multiply decimals:

  • Set up and multiply the numbers as you do with whole numbers.
  • Count the total number of decimal places in both of the factors.
  • Place the decimal point in the product so that the number of decimal places in the product is the sum of the decimal places in the factors.
  • Keep all zeros in the product when you place the decimal point. You can drop the zeros on the right once the decimal point has been placed in the product. If the number of decimal places is greater than the number of digits in the product, you can insert zeros in front of the product.

 

 

Multiply. `51.2 * 3.08`

 

A) `15769.6`

 

B) `1576.96`

 

C) `157.696`

 

D) `15.7696`

 

+ 

Show/Hide Answer

 

Multiplying by Tens

Take a moment to multiply `4.469` by `10`. Now do `4.469 * 100`. Finally, do `4.469 * 1,000`. Notice any patterns in your products?

Notice that the products keep getting greater by one place value as the multiplier (`10`, `100`, and `1,000`) increases. In fact, the decimal point moves to the right by the same number of zeros in the power of ten multiplier.

`4.469*10` `=` `44.69`        `4.469*100` `=` `446.9`        `4.469*1,000` `=` `4469.`

You can use this observation to help you quickly multiply any decimal by a power of ten (`10`, `100`, `1,000`, etc).

Example

Problem

`0.03*100=?` 

 

 

 

`0.03 * 100 =?`

 

`100` has two zeros.

 

`0.03 * 100 = 3`

 

Move the decimal point two places to the right to find the product.

Answer

`0.03 * 100 = 3`

 

 

 

Multiplying a Decimal by a Power of Ten

 

To multiply a decimal number by a power of ten (such as `10`, `100`, `1,000`, etc.), count the number of zeros in the power of ten. Then move the decimal point that number of places to the right.

 

For example, `0.054 * 100 = 5.4`. The multiplier `100` has two zeros, so you move the decimal point in `0.054` two places to the right—for a product of `5.4`.

 

Dividing Decimals

To divide decimals, you will once again apply the methods you use for dividing whole numbers. Look at the two problems below. How are the methods similar?

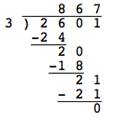
In a long division problem, the dividend is 2601. The divisor is 3. The final quotient is 867. Multiply the first part of the quotient, 8, by the divisor, which equals 24, and place it below the dividend. Subtract 24 from 26, the first two digits in the the dividend, which equals 2. Bring down the zero from the dividend to make 20. Next, multiply the 6 in the quotient by the divisor resulting in 18, which is subtracted from 20 in the line above it. This equals 2. Bring down the 1 from the dividend to make 21. 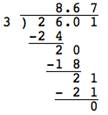Next, multiply the 7 in the quotient by the divisor resulting in 21, which is subtracted from 21 in the line above it, leaving a remainder of 0.In a long division problem, the dividend is 26.01. The divisor is 3. The final quotient is 8.67. Multiply the first part of the quotient, 8, by the divisor, which equals 24 and is placed below the dividend. Subtract 24 from 26, the first two digits in the the dividend, which equals 2. Bring down the zero from the dividend to make 20. Next, multiply the 6 in the quotient by the divisor resulting in 18, which is subtracted from 20 in the line above it. This equals 2. Bring down the 1 from the dividend to make 21. Next, multiply the 7 in the quotient by the divisor resulting in 21, which is subtracted from 21 in the line above it, leaving a remainder of 0.

Notice that the division occurs in the same way—the only difference is the placement of the decimal point in the quotient The result of a division problem. In the problem `8` ÷ `2 = 4`, `4` is the quotient. .

Example

Problem

`18.32-:8=?` 

 

 

 

 

In a long division problem, the dividend is 18.32. The divisor is 8.

 

 

Set up the problem.

 

 

 

In a long division problem, the dividend is 18.32. The divisor is 8. The final quotient is 2.29. Multiply the first part of the quotient, 2, by the divisor, which equals 16 and is placed below the dividend. Subtract 16 from 18, the first two digits in the the dividend, which equals 2. Bring down the 3 from the dividend to make 23. Next, multiply the 2 in the quotient by the divisor resulting in 16, which is subtracted from 23 in the line above it. This equals 7. Bring down the 2 from the dividend to make 72. Next, multiply the 9 in the quotient by the divisor resulting in 72, which is subtracted from 72 in the line above it, leaving a remainder of 0.

 

 

 

Divide.

 

 

In a long division problem, the dividend is 18.32. The divisor is 8. The quotient is 2.29.

 

 

Place the decimal point in the quotient. It should be placed directly above the decimal point in the dividend.

Answer

`18.32-:8 = 2.29`

 

 

But what about a case where you are dividing by a decimal, as in the problem below?

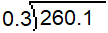
In a long division problem, the dividend is 260.1. The divisor is 0.3.

In cases like this, you can use powers of `10` to help create an easier problem to solve. In this case, you can multiply the divisor The number that is being divided into the dividend in a division problem. In the problem `8` ÷ `2 = 4`, `2` is the divisor. , `0.3`, by `10` to move the decimal point `1` place to the right. If you multiply the divisor by `10`, then you also have to multiply the dividend The number to be divided up in a division problem. In the problem `8` ÷ `2 = 4`, `8` is the dividend. by `10` to keep the quotient the same. The new problem, with its solution, is shown below.

Example

Problem

`260.1-:0.3=?` 

 

 

 

 

In a long division problem, the dividend is 260.1. The divisor is 0.3.

 

 

 

Set up the problem.

 

 

In a long division problem, the dividend shows the decimal point moved to the right one place, making it 2601. The divisor also shows the decimal point moved to the right one place, making it 3.

 

 

 

Multiply divisor and dividend by `10` to create a whole number divisor.

 

 

In a long division problem, the dividend is 2601. The divisor is 3. The final quotient is 867. Multiply the first part of the quotient, 8, by the divisor, which equals 24 and is placed below the dividend. Subtract 24 from 26, the first two digits in the the dividend, which equals 2. Bring down the 0 from the dividend to make 20. Next, multiply the 6 in the quotient by the divisor resulting in 18, which is subtracted from 20 in the line above it. This equals 2. Bring down the 1 from the dividend to make 21. Next, multiply the 7 in the quotient by the divisor resulting in 21, which is subtracted from 21 in the line above it, leaving a remainder of 0.

 

 

Divide.

Answer

`260.1-:0.3 = 867`

 

 

Often, the dividend will still be a decimal after multiplying by a power of `10`. In this case, the placement of the decimal point must align with the decimal point in the dividend.

Example

Problem

`15.275-:3.25=?` 

 

 

 

In a long division problem, the dividend is 15.275. The divisor is 3.25.

 

 

Set up the problem.

 

 

In a long division problem, the dividend shows the decimal point moved to the right two places, making it 1527.5. The divisor also shows the decimal point moved to the right two places, making it 325.

 

 

Multiply divisor and dividend by `100` to create a whole number divisor.

 

 

In a long division problem, the dividend is 1527.5. The divisor is 325. The final quotient is 4.7. Multiply the first part of the quotient, 4, by the divisor, which equals 1300 and is placed below the dividend. 1300 is subtracted from 1527, the first 4 digits in the the dividend, which equals 227. Bring down the 5 from the dividend to make 2275. Next, multiply the 7 in the quotient by the divisor resulting in 2275, which is subtracted from 2275 in the line above it, leaving a remainder of 0.

 

 

 

 

Divide. `325` goes into `1527` four times, so the number `4` is placed above the digit `7`.

 

The decimal point in the quotient is placed directly above the decimal point in the dividend.

Answer

 `15.275-:3.25 = 4.7`

 

 

 

Dividing Decimals

 

Dividing Decimals by Whole Numbers

Divide as you would with whole numbers. Then place the decimal point in the quotient directly above the decimal point in the dividend.

 

Dividing by Decimals

To divide by a decimal, multiply the divisor by a power of ten to make the divisor a whole number. Then multiply the dividend by the same power of ten. You can think of this as moving the decimal point in the dividend the same number of places to the right as you move the decimal point in the divisor.

 

Then place the decimal point in the quotient directly over the decimal point in the dividend. Finally, divide as you would with whole numbers.

 

 

Divide: `25.095-:0.5.`

 

A) `5,019`

 

B) `501.9`

 

C) `50.19`

 

D) `0.5019`

 

+ 

Show/Hide Answer

 

Dividing by Tens

Recall that when you multiply a decimal by a power of ten (`10`, `100`, `1,000`, etc.), the placement of the decimal point in the product will move to the right according to the number of zeros in the power of ten. For instance, `4.12 * 10 = 41.2`.

Multiplication and division are inverse operations, so you can expect that if you divide a decimal by a power of ten, the decimal point in the quotient will also correspond to the number of zeros in the power of ten. The difference is that the decimal point moves to the right when you multiply; it moves to the left when you divide.

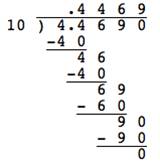
In a long division problem, the dividend is 4.4690. The divisor is 10. The final quotient is .4469. Multiply the first part of the quotient, .4, by the divisor, which equals 40 and is placed below the dividend. Subtract 40 from 44, the first 2 digits in the the dividend, which equals 4. Bring down the 6 from the dividend to make 46. Next, multiply the 6 in the quotient by the divisor resulting in 60, which is subtracted from 69 in the line above it. This equals 9. Bring down the 0 from the dividend to make 90. Next, multiply the 9 in the quotient by the divisor resulting in 90, which is subtracted from 90 in the line above it, leaving a remainder of 0. In a long division problem, the dividend is 4.46900. The divisor is 100. The final quotient is .04469. Multiply the first part of the quotient, .04, by the divisor, which equals 400 and is placed below the dividend. Subtract 400 from 4.46, the first 2 digits in the the dividend, which equals 46. Bring down the 9 from the dividend to make 469. Next, multiply the 4 in the quotient by the divisor resulting in 400, which is subtracted from 469 in the line above it. This equals 69. Bring down the 0 from the dividend to make 690. Next, multiply the 6 in the quotient by the divisor resulting in 600, which is subtracted from 690 in the line above it. This equals 90. Bring down the 0 from the dividend to make 900. Next, multiply the 9 in the quotient by the divisor resulting in 900, which is subtracted from 900 in the line above it, leaving a remainder of 0. 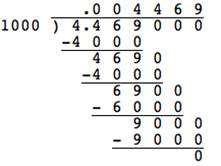In a long division problem, the dividend is 4.469000. The divisor is 1000. The final quotient is .004469. Multiply the first part of the quotient, .004, by the divisor, which equals 4000 and is placed below the dividend. Subtract 4000 from 4.469, the first 4 digits in the the dividend, which equals 4690. Bring down the 0 from the dividend to make 4690. Next, multiply the 4 in the quotient by the divisor resulting in 4000, which is subtracted from 4690 in the line above it. This equals 690. Bring down the 0 from the dividend to make 6900. Next, multiply the 6 in the quotient by the divisor resulting in 6000, which is subtracted from 6900 in the line above it. This equals 900. Bring down the 0 from the dividend to make 9000. Next, multiply the 9 in the quotient by the divisor resulting in 9000, which is subtracted from 9000 in the line above it, leaving a remainder of 0.

In the examples above, notice that each quotient still contains the digits `4469`—but as another `0` is added to the end of each power of ten in the divisor, the decimal point moves an additional place to the left in the quotient.

Dividing by Powers of Ten

 

To divide a decimal by a power of ten (`10`, `100`, `1,000`, etc.), count the number of zeros in the divisor. Then move the decimal point in the dividend that number of decimal places to the left; this will be your quotient.

 

 

Example

Problem

`31.05-:10=?` 

 

 

 

`31.05-:10=?`

 

`10` has one zero.

 

 `31.05-:10 = 3.105`

 

 

Move the decimal point one place to the left in the dividend; this is the quotient.

Answer

 `31.05-:10 = 3.105`

 

 

 

Divide. `0.045-:100` 

 

A) `0.00045`

 

B) `0.045`

 

C) `4.5`

 

D) `4,500`

 

+ 

Show/Hide Answer

 

Solving Problems by Multiplying or Dividing Decimals

Now let’s return to the two problems from the beginning of this section. You know how to multiply and divide with decimals now. Let’s put that knowledge to the test.

Example

Problem

 

 

 

A couple eats dinner at a Japanese steakhouse. The bill for the meal totals `$58.32`—which includes a tax of `$4.64`. To calculate the tip, they can double the tax. How much tip should the couple leave?

 

 

 

 

Set up a multiplication problem.

 

 

 

 

 

 

Multiply `4.64` by `2`.

 

 

 

 

 

Count the number of decimal places in the two factors, and place the decimal point accordingly.

Answer

The couple should leave a tip of `$9.28`.

 

 

 

Example

Problem

 

 

 

 

Andy just sold his van that averaged `20` miles per gallon of gasoline. He bought a new pickup truck and took it on a trip of `614.25` miles. He used `31.5` gallons of gas for the trip. Did Andy get better gas mileage with the new truck?

 

In a long division problem, the dividend is 614.25. The divisor is 31.5.

 

 

 

Set up a division problem.

 

 

In a long division problem, the dividend shows the decimal point moved to the right one place, making it 6142.5. The divisor also shows the decimal point moved to the right one place, making it 315.

 

 

Make the divisor a whole number by multiplying by `10`; do the same to the dividend.

 

 

 

In a long division problem, the dividend is 6142.5. The divisor is 315. The final quotient is 19.5. Multiply the first part of the quotient, 1, by the divisor, which equals 315 and is placed below the dividend. Subtract 315 from 614, the first 3 digits in the the dividend, which equals 299. Bring down the 2 from the dividend to make 2992. Next, multiply the 9 in the quotient by the divisor resulting in 2835, which is subtracted from 2992 in the line above it, which equals 157. Bring down the 5 from the dividend to make 1575. Next, multiply the 5 in the quotient by the divisor resulting in 1575, which is subtracted from 1575 in the line above it, leaving a remainder of 0.

 

 

Divide. Insert a decimal point in the quotient so that it is directly above the decimal point in the dividend.

Answer

Andy gets `19.5` miles per gallon now. He used to get `20` miles per gallon. He does not get better gas mileage with the new truck.

Summary

Learning to multiply and divide with decimals is an important skill. In both cases, you work with the decimals as you have worked with whole numbers, but you have to figure out where the decimal point goes. When multiplying decimals, the number of decimal places in the product is the sum of the decimal places in the factors. When dividing by decimals, move the decimal point in the dividend the same number of places to the right as you move the decimal point in the divisor. Then place the decimal point in the quotient above the decimal point in the dividend.