Ordenando y redondeando decimales
Objetivos de aprendizaje
· Usar la recta numérica como ayuda para comparar decimales.
· Comparar decimales, empezando con sus dígitos de izquierda a derecha.
· Usar < o > para comparar decimales.
· Redondear un decimal dado a una posición específica.
Introducción
Los números decimales son una combinación de números enteros y números que se encuentran entre los números enteros. A veces es importante poder comparar decimales para saber cuál es mayor. Por ejemplo, si alguien corrió los 100 metros planos en 10.57 segundos, y alguien más los corrió en 10.67 segundos, puedes comparar los decimales para determinar qué tiempo es más rápido. Saber cómo comparar decimales requiere el entendimiento del valor de posición decimal, y es similar a comprar números enteros.
Cuando trabajamos con decimales, hay veces que no se necesita un número preciso. En tal caso, es útil redondear números decimales. Por ejemplo, si la bomba de una gasolinera muestra que llenaste el tanque del carro de un amigo con 16.478 galones de gasolina, podrías querer redondear el número y decirle a tu amigo que le pusiste 16.5 galones.
Puedes usar la recta numérica para comparar decimales. El número que esté más hacia la derecha es el mayor. Examina éste método en el ejemplo siguiente.
| Ejemplo | ||
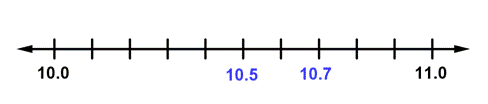
| Problema | Usa < o > en lugar de [ ] para escribir un enunciado correcto: 10.5 [ ] 10.7. | |
|
Aquí, los dígitos en el lugar de las décimas son diferentes. Ambos números están graficados en la recta numérica que va desde 10.0 a 11.0. Como 10.5 está a la izquierda de 10.7 en la recta numérica, 10.5 es menor que (<) 10.7.
| ||
| Respuesta | 10.5 < 10.7 | |
Otra forma de comparar decimales es comparar los dígitos en cada número, empezando con el lugar de posición mayor, que es el de la izquierda. Cuando un dígito en un número decimal es mayor que el dígito correspondiente en el otro número, entonces ése número decimal es mayor.
Por ejemplo, primero compara los dígitos de las décimas. Si son iguales, continúa con el lugar de las centésimas. Si esos dígitos no son iguales, el decimal con el dígito mayor es el número decimal mayor. Observa cómo se hace esto en los ejemplos siguientes.
| Ejemplo | ||
| Problema | Usa < o > en lugar de [ ] para escribir un enunciado correcto: 35.689 [ ] 35.679. | |
|
Aquí, los números en las decenas, las unidades, y las décimas, 35.6, son iguales. Sin embargo, los dígitos en el lugar de las centésimas difieren. Ya que 8 es mayor que 7, 35.689 es mayor que 35.679.
| ||
| Respuesta | 35.689 > 35.679 | |
Si más de dos dígitos difieren en ambos números, toma en cuenta el dígito que en el valor de posición mayor. Observa el siguiente ejemplo en el que se comparan dos cantidades de dinero.
| Ejemplo | ||
| Problema | Usa < o > en lugar de [ ] para escribir un enunciado correcto: $45.67 [ ] $45.76. | |
|
Aquí, el valor de posición que determina qué cantidad es mayor no es el de las centésimas, sino el de las décimas. Como 6 décimas es menor que 7 décimas, $45.67 es menor que $45.76.
| ||
| Respuesta | $45.67 < $45.76 | |
Si un número tiene más decimales que el otro, puedes usar 0s como referencia en el número con menos decimales para ayudarte a comparar. Por ejemplo, si comparas 4.75 y 4.7 puede ser más fácil escribir 4.7 como 4.70 para que ambos números tengan tres dígitos. Observa que añadir el 0 extra no cambia el valor del decimal; le estás sumando 0 centésimas al número. Puedes añadir 0s como referencia siempre y cuando los pongas al final del número, a la derecha del punto decimal.
Esto se demuestra en el siguiente ejemplo.
| Ejemplo | ||
| Problema | Usa < o > en lugar de [ ] para escribir un enunciado correcto: 5.678 [ ] 5.6. | |
| Aquí, puedes insertar dos ceros en el lugar de las centésimas y las milésimas de 5.6 para que tengas el mismo número de dígitos para cada número. Luego, comparas los dígitos. Busca el valor de posición mayor que tenga valores distintos en cada número. En éste caso es el lugar de las centésimas.
Como 7 es mayor que 0, 5.678 es mayor que 5.600.
| ||
| Respuesta | 5.678 > 5.6 | |
| Estrategias para comparar decimales
· Usa una recta numérica para ayudarte a comparar decimales, como hacías con los números enteros. · Compara decimales empezando con sus dígitos de izquierda a derecha. Cuando dos dígitos son distintos, el que tenga el dígito más grande será el número mayor.
|
| Usa < o > en lugar de [ ] para escribir un enunciado correcto: 45.675 [ ] 45.645.
A) 45.675 < 45.645
B) 45.675 > 45.645
|
Redondear decimales es igual que redondear números enteros. De igual forma, redondeas un número a cierto valor de posición. Todo hacia la derecha de cierto valor de posición se vuelve cero, y el dígito en la posición dada se conserva o se incrementa en uno.
Con los decimales, puedes “eliminar” los ceros al final del número sin cambiar su valor. Por ejemplo, 0.20 = 0.2, como ![]() se simplifica a
se simplifica a ![]() . Claro que no puedes deshacerte de los ceros antes del punto decimal: 200 ≠ 20.
. Claro que no puedes deshacerte de los ceros antes del punto decimal: 200 ≠ 20.
Los ceros que aparecen al final de un número decimal se llaman ceros a la derecha.
| Eliminando ceros con números enteros y decimales | |
| Eliminar ceros al final de números enteros cambia el valor del número. |
7200 ≠ 72
200,000 ≠ 2
|
|
Eliminar ceros al final de números enteros no cambia el valor del número.
|
36.00 = 36
1.00000 = 1
|
Una manera de pensar en esto es considerando el número “treinta y seis dólares.” Esta cantidad puede escribirse de dos maneras:
$36 = $36.00
Cualquier cero al final de un número decimal puede ser eliminado:
18.25000 = 18.2500 = 18.250 = 18.25
| Ejemplo | ||
| Problema | Un atleta corrió una carrera en 7.354 segundos. ¿Cuál es el tiempo del atleta, redondeado a la décima de segundo más cercana? | |
| 7.354
7.354 → 7.400
7.400
7.4
| Observa el primer dígito a la derecha del dígito de las décimas.
Como 5 = 5, redondea hacia arriba el 3, a 4.
Cambia a ceros todos los dígitos a la derecha del valor de posición dado. Este es un paso intermedio que no es necesario escribir.
Como 0.400 = 0.4, los ceros no son necesarios y pueden eliminarse.
| |
| Respuesta 7.354 redondeado a la décima más cercana es 7.4. | ||
En el ejemplo anterior, el dígito junto al valor de posición seleccionado es 5, por lo que redondeas hacia arriba. Veamos un caso en donde el dígito junto al valor de posición seleccionado es menor que 5.
| Ejemplo | ||
| Problema | Redondea 7.354 a la centésima más cercana. | |
|
7.354
7.354 → 7.350
7.35 |
Observa el primer dígito a la derecha del dígito de las centésimas.
Como 4 < 5, deja el 5 como está.
Los ceros a la derecha del valor de posición seleccionado no son necesarios y pueden eliminarse.
| |
| Respuesta 7.354 redondeado a la centésima más cercana es 7.35. | ||
Algunas veces se te pide redondear un número decimal a un valor de posición que está en la parte del número entero. Recuerda que no puedes eliminar los ceros a la izquierda del punto decimal.
| Ejemplo | ||
| Problema | Redondea 1,294.6374 a la centésima más cercana. | |
|
1,294.6374
1,294.6374 → 1,300.000
1,300
|
Observa el primer dígito a la derecha del dígito de las centésimas.
9 es mayor que 5, redondea hacia arriba el 2, a 3.
Los ceros a la izquierda del decimal deben incluirse.
Los ceros a la derecha del valor de posición seleccionado no son necesarios y pueden eliminarse.
| |
| Respuesta 1,294.6374 redondeado a la centésima más cercana es 1,300. | ||
| Consejos para redondear decimales
Cuando redondeas, todo lo que está a la derecha del valor de posición dado se vuelve cero, y el valor del dígito en el valor de posición se conserva o se redondea una unidad hacia arriba. Los ceros a la derecha después del punto decimal pueden ser eliminados.
|
| Redondea 10.473 a la décima más cercana.
A) 10.47
B) 10.4
C) 10.473
D) 10.5
|
Sumario
Ordenar, comparar, y redondear decimales son habilidades importantes. Puedes calcular los tamaños relativos de dos números decimales usando la recta numérica y comparando los dígitos en el mismo valor de posición en cada uno de los números. Para redondear un decimal a un valor de posición específico, cambia a cero todos los dígitos a la derecha de la posición dada, y luego redondea el dígito en dicha posición ya sea hacia arriba o hacia abajo. Los ceros a la derecha después del punto decimal pueden ser eliminados.