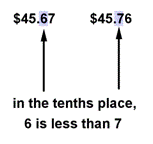Ordering and Rounding Decimals
Decimal numbersDecimal numbers are numbers whose place value is based on `10`s, including whole numbers and decimal fractions, which have decimal points and digits to the right of the decimal point. The numbers `18`, `4.12` and `0.008` are all decimal numbers. are a combination of whole numbers and numbers between whole numbers. It is sometimes important to be able to compare decimals to know which is greater. For example, if someone ran the `100`-meter dash in `10.57` seconds, and someone else ran the same race in `10.67` seconds, you can compare the decimals to determine which time is faster. Knowing how to compare decimals requires an understanding of decimal place value, and is similar to comparing whole numbers.
When working with decimals, there are times when a precise number isn’t needed. When that’s true, rounding decimal numbers is helpful. For example, if the pump at the gas station shows that you filled a friend’s car with `16.478` gallons of gasoline, you may want to round the number and just tell her that you filled it with `16.5` gallons.
You can use a number line to compare decimals. The number that is further to the right is greater. Examine this method in the example below.
|
Example |
||
|
Problem
|
Use `<` or `>` for `[\ ]` to write a true sentence: `10.5 [\ ] 10.7`. |
|
|
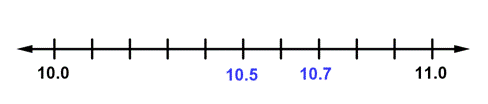
Here, the digits in the tenths places differ. The numbers are both plotted on a number line ranging from `10.0` to `11.0`. Because `10.5` is to the left of `10.7` on the number line, `10.5` is less than (<) `10.7`.
|
||
|
Answer |
`10.5<10.7` |
|
Another approach to comparing decimals is to compare the digits in each number, beginning with the greatest place value, which is on the left. When one digit in a decimal number is greater than the corresponding digit in the other number, then that decimal number is greater.
For example, first compare the tenths digits. If they are equal, move to the hundredths place. If these digits are not equal, the decimal with the greater digit is the greater decimal number. Observe how this is done in the examples below.
|
Example |
||
|
Problem
|
Use `<` or `>` for `[ \ ]` to write a true sentence: `35.689 [\ ] 35.679`. |
|
|
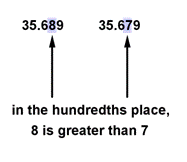
Here, the numbers in the tens, ones, and tenths places, `35.6`, are the same. However, the digits in the hundredths places differ. Because `8` is greater than `7`, `35.689` is greater than `35.679`.
|
||
|
Answer |
`35.689>35.679` |
|
If more than two digits in the two numbers differ, focus on the digit in the greatest place value. Look at this example in which two sums of money are compared.
|
Example |
||
|
Problem
|
Use `<` or `>` for `[\ ]` to write a true sentence: `$45.67 [\ ] $45.76`. |
|
|
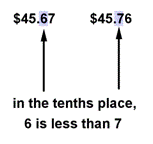
Here, the place value that determines which amount is greater is not the hundredths place, but the tenths place. Because `6` tenths is less than `7` tenths, `$45.67` is less than `$45.76`.
|
||
|
Answer |
`$45.67<$45.76` |
|
If one number has more decimal places than another, you may use `0`s as placeholders in the number with fewer decimal places to help you compare. For example, if you are comparing `4.75` and `4.7`, you may find it helpful to write `4.7` as `4.70` so that each number has three digits. Note that adding this extra `0` does not change the value of the decimal; you are adding `0` hundredths to the number. You can add placeholder `0`s as long as you remember to add the zeros at the end of the number, to the right of the decimal point.
This is demonstrated in the example below.
|
Example |
||
|
Problem
|
Use `<` or `>` for `[\ ]` to write a true sentence: `5.678 [\ ] 5.6`. |
|
|
Here, you can insert two zeros in the hundredths and thousandths places of `5.6` so that you have the same number of digits for each. Then, you can compare digits. Look for the greatest place value that has different values in each number. Here, it is the hundredths place.
Because `7` is greater than `0`, `5.678` is greater than `5.600`.
|
||
|
Answer |
`5.678>5.6` |
|
|
Strategies for Comparing Decimals
|
|
Use `<` or `>` for `[\ ]` to write a true sentence: `45.675 [\ ] 45.645`.
A) `45.675<45.645`
B) `45.675>45.645`
|
Rounding with decimals is like rounding with whole numbers. As with whole numbers, you round a number to a given place value. Everything to the right of the given place value becomes a zero, and the digit in the given place value either stays the same or increases by one.
With decimals, you can “drop off” the zeros at the end of a number without changing its value. For example, `0.20 = 0.2`, as `20/100` simplifies to `2/10`. Of course, you cannot drop zeros before the decimal point: `200!=20`.
The zeros that occur at the end of a decimal number are called trailing zerosA placeholder `0` that occurs after the final non-`0` digit in a decimal number. In the number `22.0900`, the `0`s in the thousandths and ten-thousandths places are trailing zeros..
|
Dropping Zeros with Whole Numbers and Decimals |
|
|
Dropping zeros at the end of a whole number changes the value of a number. |
`7200!=72`
`200,000!=2`
|
|
Dropping zeros at the end of a decimal does not change the number’s value.
|
`36.00 = 36`
`1.00000 = 1`
|
One way to think of it is to consider the number “thirty-six dollars.” This amount can be written equally well one of two ways:
`$36 = $36.00`
Any zero at the very end of a decimal number can be dropped:
`18.25000 = 18.2500 = 18.250 = 18.25`
|
Example |
||
|
Problem
|
A sprinter ran a race in `7.354` seconds. What was the sprinter's time, rounded to the nearest tenth of a second? |
|
|
Look at the first digit to the right of the tenths digit.
Since `5 = 5`, round the `3` up to `4`.
Change all digits to the right of the given place value into zeros. This is an intermediate step that you don’t actually write down.
Since `0.400 = 0.4`, the zeros are not needed and should be dropped.
|
||
|
Answer `7.354` rounded to the nearest tenth is `7.4`. |
||
In the example above, the digit next to the selected place value is `5`, so you round up. Let’s look at a case in which the digit next to the selected place value is less than `5`.
|
Example |
||
|
Problem |
Round `7.354` to the nearest hundredth. |
|
|
Look at the first digit to the right of the hundredths digit.
Since `4<5`, leave `5` as is.
The zeros to the right of the given place value are not needed and should be dropped.
|
||
|
Answer `7.354` rounded to the nearest hundredth is `7.35`. |
||
Sometimes you’re asked to round a decimal number to a place value that is in the whole number part. Remember that you may not drop zeros to the left of the decimal point.
|
Example |
||
|
Problem |
Round `1,294.6374` to the nearest hundred. |
|
|
Look at the first digit to the right of the hundreds place.
`9` is greater than `5`, so round the `2` up to `3`.
Zeros to the left of the decimal must be included.
Zeros to the right of the decimal can be dropped and should be dropped.
|
||
|
Answer `1,294.6374` rounded to the nearest hundred is `1,300`.
|
||
|
Tip on Rounding Decimals
When you round, everything to the right of the given place value becomes a zero, and the digit in the given place value either stays the same or rounds up one. Trailing zeros after the decimal point should be dropped.
|
|
Round `10.473` to the nearest tenth.
A) `10.47`
B) `10.4`
C) `10.473`
D) `10.5`
|
Ordering, comparing, and rounding decimals are important skills. You can figure out the relative sizes of two decimal numbers by using number lines and by comparing the digits in the same place value of the two numbers. To round a decimal to a specific place value, change all digits to the right of the given place value to zero, and then round the digit in the given place value either up or down. Trailing zeros after the decimal point should be dropped.
