Multiplicando Fracciones y Números Mixtos

 

 

Objetivos de Aprendizaje

·         Multiplicar dos o más fracciones.

·         Multiplicar una fracción por un número entero.

·         Multiplicar dos o más números mixtos.

·         Resolver problemas de aplicación que requieren la multiplicación de fracciones o números mixtos.

 

Introducción

 

Así como sumas, restas, multiplicas, y divides cuando trabajas con números enteros, también usas éstas operaciones cuando trabajas con fracciones. Muchas veces es necesario multiplicar fracciones y números mixtos. Por ejemplo, ésta receta sirve para hornear 4 empanada:

 

5 tazas de galletas integrales        8 tazas de azúcar

 tazas de mantequilla             cucharadas de vainilla

 

Suponiendo que sólo quieres hacer 2 empanadas. Puedes multiplicar todos los ingredientes por , ya que sólo se necesitan un medio de los ingredientes. Después de aprender cómo multiplicar una fracción por otra fracción, un número entero o un número mixto, vas a poder calcular los ingredientes para hacer 2 empanadas.

 

Multiplicando Fracciones

 

Cuando multiplicas una fracción por una fracción, estás encontrando la “fracción de una fracción.” Supongamos que tienes  de dulce y quieres encontrar  de :

 

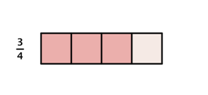
U02_L2_T1_text_image5

 

 Dividiendo cada cuarto a la mitad, puedes divide el dulce en 8 piezas.

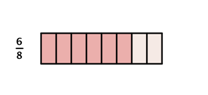
                                    U02_L2_T1_text_image6

Ahora, toma la mitad de ellas para obtener .

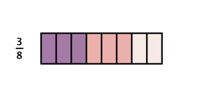
                                    U02_L2_T1_text_image7

 

En los dos casos anteriores, para encontrar la respuesta, puedes multiplicar numeradores con numeradores y denominadores con denominadores.

 

Multiplicando Dos Fracciones

 

 

Ejemplo:

 

 

Multiplicando Más de Dos Fracciones

 

 

Ejemplo:

 

 

 

 

Ejemplo

Problema

Multiplica.

 

Multiplica los numeradores y multiplica los denominadores.

 

Simplifica si es posible. Ésta fracción ya está reducida a su mínima expresión.

 

Respuesta

 

 

Si el producto resultante necesita ser simplificado a su mínima expresión, divide el numerador y el denominador entre factores comunes.

 

 

Ejemplo

Problema

Multiplica. Simplifica el resultado.

 

Multiplica los numeradores y multiplica los denominadores.

 

Simplifica si es posible

 

Simplifica dividiendo el numerador y el denominador entre el factor común 2.

 

Respuesta

 

 

 

También puedes simplificar el problema antes de multiplicar, dividiendo entre factores comunes.

 

Ejemplo

Problema

 

Multiplica. Simplifica el resultado.

 

 

 

          

Reordena los numeradores de tal forma que puedas ver la fracción que tiene un factor común.

 

Simplifica.

 

Respuesta

 

 

 

No es necesario que uses el atajo de “primero simplificar” pero esto podría hacer más fácil tu trabajo porque mantiene más pequeños los números en el numerador y en el denominador mientras que los operas.

 

 

 Multiplica. Simplifica el resultado.

A)

 

B)

 

C)

 

D)

 

Mostrar/Ocultar Respuesta

A)

Incorrecto.  es una fracción equivalente a la respuesta correcta , pero no está reducida a su mínima expresión. Debes dividir el numerador y el denominador entre el factor común 3. La respuesta correcta es .

 

B)

Incorrecto. Probablemente sumaste los numeradores (3 + 1) y sumaste los denominadores (4 + 3) en lugar de multiplicarlos. La respuesta correcta es .

 

C)

Correcto. Una forma de encontrar la solución es multiplicar el numerador por el numerador y el denominador por el denominador , luego simplifica: .

 

D)

Incorrecto. Probablemente encontraste un común denominador, multiplicaste correctamente, pero olvidaste simplificar. Encontrar un común denominador no es necesario y hace más difícil la multiplicación porque trabajas con números más grandes que lo necesario. La respuesta correcta es .

 

 

 

Multiplicando una Fracción por un Número Entero

 

Cuando trabajas con fracciones y números enteros, es útil escribir el número entero como una fracción impropia (una fracción donde el numerador es mayor o igual que el denominador). Todos los números pueden escribirse con un “1” en el denominador. Por ejemplo: , , y . Recuerda que el denominador te dice cuántas partes hay de la unidad, y el numerador te dice cuántas partes tienes.

 

Multiplicando una Fracción por un Número Entero

 

 

Ejemplo:

 

 

 

Muchas veces cuando multiplicas un número entero y una fracción, el producto resultante tendrá una fracción impropia. Se pueden escribir las fracciones impropias como un número mixto para el resultado final.

 

 

Ejemplo

Problema

Multiplica. Simplifica la solución y escríbela como un número mixto.

 

Reescribe 7 como la fracción impropia .

 

Multiplica los numeradores y multiplica los denominadores.

 

Reescribe como un número mixto. .

 

Respuesta

 

 

 

 

Ejemplo

Problema

Multiplica. Simplifica la solución y escríbela como un número mixto.

 

Rescribe 4 como la fracción impropia .

 

Multiplica los numeradores y multiplica los denominadores.

 

 

Simplifica.

 

Respuesta

 3

 

 

 

 

  Multiplica. Simplifica la solución y escríbela como un número mixto.

 

A)

 

B)

 

C)

 

D)

 

Mostrar/Ocultar Respuesta

A)

Incorrecto. Probablemente sumaste numerador con numerador y denominador con denominador, para obtener , que es el número mixto . Asegúrate que multiplicas numerador con numerador y denominador con denominador. Al multiplicar los dos números obtienes , y como 15 ÷ 6 = 2R3, el número mixto es . La parte fraccionaria se simplifica como . La respuesta correcta es .

 

B)

Correcto. Multiplicar los dos números resulta en , y como 15 ÷ 6 = 2R3, el número mixto es . La parte fraccionaria se simplifica como .

 

C)

Incorrecto. Multiplicar los numeradores con los numeradores y los denominadores con los denominadores resulta en la fracción impropia , pero necesitas expresar ésto como un número mixto. La respuesta correcta es .

 

D)

Incorrecto. Probablemente sumaste los numeradores y los pusiste sobre el denominador 6. Asegúrate que multiplicas numerador con numerador y denominador con denominador. Al multiplicar los dos números obtienes , y como 15 ÷ 6 = 2R3, el número mixto es . La parte fraccionaria se simplifica como . La respuesta correcta es .

 

 

 

Multiplicando Números Mixtos

 

Si quieres multiplicar dos números mixtos, o una fracción con un número mixto, puedes reescribir un número mixto como una fracción impropia.

 

Entonces, para multiplicar dos números mixtos, reescribe cada uno como una fracción impropia y luego multiplica normalmente. Multiplica numeradores con numeradores y denominadores con denominadores y simplifica. Y, como antes, cuando simplificas, si la solución resulta una fracción impropia, conviértela a un número mixto.

 

 

Ejemplo

Problema

Multiplica. Simplifica la solución y escríbela como un número mixto.

 

Convierte  a una fracción impropia. 5 • 2 + 1 = 11, y el denominador es 5.

 

Convierte  a una fracción impropia. 2 • 4 + 1 = 9, y el denominador es 2.

 

Reescribe el problema de multiplicación, usando fracciones impropias.

 

Multiplica los numeradores y multiplica los denominadores.

 

Escribe como un número mixto.

 

Respuesta

 

 

 

 

 

Ejemplo

Problema

Multiplica. Simplifica la solución y escríbela como un número mixto.

 

Convierte  a una fracción impropia. 3 • 3 + 1 = 10, y el denominador es 3.

 

Reescribe el problema de multiplicación, usando la fracción impropia en lugar del número mixto.

 

Multiplica los numeradores y multiplica los denominadores.

 

Reescribe como un número mixto.

con un residuo de 4.

 

Simplifica la parte fraccional a su mínima expresión dividiendo el numerador el denominador entre el factor común 2.

 

Respuesta

 

 

Como vimos anteriormente, algunas veces es útil buscar factores comunes en el numerador y el denominador antes de simplificar los productos.

 

Ejemplo

Problema

Multiplica. Simplifica la solución y escríbela como un número mixto.

 

Convierte  a una fracción impropia. 5 • 1 + 3 = 8, y el denominador es 5.

 

Convierte  a una fracción impropia. 4 • 2 + 1 = 9, y el denominador es 4.

 

 

 

Reescribe el problema de multiplicación, usando fracciones impropias

 

Reordena los numeradores de tal forma que puedas ver una fracción que tenga un factor común.

Simplifica.

 

 

         

 

Multiplica.

 

 

Escribe como una fracción mixta.

 

Respuesta

 

 

 

En el último ejemplo, la misma solución se encontraría si multiplicas los numeradores y multiplicas los denominadores sin quitar el factor común. Sin embargo, obtendrías , y luego tendrías que simplificar más para obtener la solución final.

 

 

 Multiplica. Simplifica la solución y escríbela como un número mixto.

 

A)

 

B)

 

C)

 

D)

 

Mostrar/Ocultar Respuesta

A)

Incorrecto. Probablemente escribiste los números mixtos como fracciones impropias. Probablemente también multiplicaste correctamente los numeradores y los denominadores. Sin embargo, ésta fracción impropia todavía se puede reescribir como un número mixto y simplificar. Dividiendo 80 ÷15 = 5 con un residuo de 5 o , luego simplificando la parte fraccional, la respuesta correcta es .

 

B)

Incorrecto. Probablemente escribiste los números mixtos como fracciones impropias. Probablemente también multiplicaste correctamente los numeradores y los denominadores, y escribiste el resultado como un número mixto. Sin embargo, el número mixto no está reducido a su mínima expresión.  puede ser simplificado como  dividiendo el numerador y el denominador entre el factor común 5. La respuesta correcta es .

 

C)

Incorrecto. Éste es el resultado de sumar ambos números. Para multiplicar, reescribe cada número mixto como una fracción impropia:  y . Luego, multiplica los numeradores con los numeradores y los denominadores con los denominadores: . Luego, escribe la fracción impropia resultante como un número mixto: . Finalmente, simplifica la parte fraccional dividiendo el numerador y el denominador entre el factor común, 5. La respuesta correcta es .

 

D)

Correcto. Primero, reescribe cada número mixto como una fracción impropia:  y . Luego, multiplica los numeradores con los numeradores y los denominadores con los denominadores: . Luego, escribe la fracción impropia resultante como un número mixto: . Finalmente, simplifica la parte fraccional dividiendo el numerador y el denominador entre el factor común, 5.

 

 

 

Resolviendo Problemas Multiplicando Fracciones y Números Mixtos

 

Ahora que sabes cómo multiplicar una fracción con otra fracción, por un número entero, o por un número mixto, puedes usar éste conocimiento para resolver problemas que implican la multiplicación de cantidades fraccionales. Por ejemplo, ahora puedes calcular los ingredientes necesarios para hornear 2 empanadas.

 

 

Ejemplo

Problema

5 tazas de galletas integrales       8 T. azúcar

 tazas de mantequilla            cucharadas de vainilla

La receta de la izquierda es para hacer 4 empanadas. Encuentra los ingredientes necesarios para hacer sólo 2 empanadas.

 

 

Como la receta es para 4 empanadas, puedes multiplicar cada uno de los ingredientes por  para encontrar las medidas para 2 empanadas.

 

 

                   

 

 tazas de galletas integrales.

 

5 tazas de galletas integrales: Como el resultado es una fracción impropia, reescribe  como la fracción impropia .

 

 

 

                                               

 

 

4 tazas de azúcar

 

8 T. azúcar:  Éste es otro ejemplo de un número entero multiplicado por una fracción.

 

 

 

               

 

 tazas de mantequilla.

 

 tazas de mantequilla: Necesitas multiplicar un número mixto por una fracción. Entonces, primero reescribe  como la fracción impropia :  2 • 1 + 1, y el denominador es 2. Luego, reescribe el problema de multiplicación usando la fracción impropia en lugar del número mixto. Multiplica.

 

 

                      

 

 cucharadas de vainilla.

 

 cucharadas de vainilla: Aquí, multiplicas una fracción por una fracción.

Respuesta

Los ingredientes necesarios para 2 empanadas son:

 tazas de galletas integrales

4 tazas de azúcar

 tazas de mantequilla

 cucharadas de vainilla

 

 

A veces, un problema indica que se necesita la multiplicación por una fracción usando frases como “la mitad de,” “un tercio de,” o “ de.”

 

Ejemplo

Problema

El costo de unas vacaciones es de $4,500 y se requiere que pagues  de ésa cantidad para reservar el viaje. ¿Cuánto tendrás que pagar cuando reserves el viaje?

 

Necesitas encontrar  de 4,500. “De” te dice que multipliques.

 

Convierte 4,500 a una fracción impropia escribiéndolo con un 1 en el denominador.

 

 

Divide.

 

900

Simplifica.

 

Respuesta

Necesitarás pagar $900 cuando reserves tu viaje.

 

 

Ejemplo

Problema

U02_L2_T1_text_image8

El diagrama de pastel de la izquierda representa la parte fraccional de tus actividades diarias. Dado que un día tiene 24 horas, ¿cuántas horas dedicas a dormir?, ¿a la escuela?, ¿a comer? Usa el diagrama de pastel para determinar tus respuestas.

 

Dormir es  del diagrama, por lo que el número de horas usadas para dormir es  de 24.

 

Reescribe 24 como una fracción impropia con denominador 1.

 

8 horas de sueño

Multiplica numeradores y multiplica denominadores. Simplifica  como 8.

 

Ir a la escuela es  del diagrama, por lo que el número de horas usadas para ir a la escuela es  de 24.

 

Reescribe 24 como una fracción impropia con denominador 1.

 

4 horas de escuela

Multiplica numeradores y multiplica denominadores. Simplifica como 4.

 

Comer es  del diagrama, por lo que el número de horas usadas para comer es  de 24.

 

Reescribe 24 como una fracción impropia con denominador 1.

 

2 horas para comer

Multiplica numeradores y multiplica denominadores. Simplifica como 2.

Respuesta

Horas usadas:

dormir: 8 horas

ir a la escuela: 4 horas

comer: 2 horas

 

 

Neil compró una docena (12) de huevos. Usó para el desayuno, ¿Cuántos huevos le quedan?

 

A)                8

B)                4

C)               9

D)               3

 

Mostrar/Ocultar Respuesta

A) 8

Correcto.  de 12 es 4 (), por lo que usó 4 huevos 12 – 4 = 8, y le quedan 8 huevos.

 

B) 4

Incorrecto.  de 12 es 4, pero eso equivale al número de huevos que usó Neil, no cuántos huevos le quedan. Necesitas restar 4 de 12 para encontrar el número de huevos restantes. La respuesta correcta es

 

C) 9

Incorrecto. Probablemente incorrectamente encontraste que  de 12 es 3.  de 12 es 4, y luego 12 - 4 = 8. La respuesta correcta es 8.

 

D) 3

Incorrecto. Necesitas encontrar  de 12, que es 4. Luego, restar 4 de 12 para obtener los 8 huevos que sobran.

 

 

Sumario

 

Multiplicas dos fracciones multiplicando los numeradores con los numeradores y los denominadores con los denominadores. A veces el resultado del producto no estará reducido a su mínima expresión, por lo que también debes simplificar. Si una o las dos fracciones son números enteros o números mixtos, primero reescribe cada una como una fracción impropia. Luego multiplica normalmente, y simplifica.