Comparing Fractions

Learning Objectives

Introduction

You often need to know when one fraction is greater or less than another fraction. Since a fraction is a part of a whole, to find the greater fraction you need to find the fraction that contains more of the whole. If the two fractions simplify to fractions with a common denominatorA number that is a multiple of all of the denominators in a group of fractions., you can then compare numerators. If the denominators are different, you can find a common denominator first and then compare the numerators.

Determining Equivalent Fractions

Two fractions are equivalent fractionsTwo or more fractions that name the same part of the whole. when they represent the same part of a whole. Since equivalent fractions do not always have the same numerator and denominator, one way to determine if two fractions are equivalent is to find a common denominator and rewrite each fraction with that denominator. Once the two fractions have the same denominator, you can check to see if the numerators are equal. If they are equal, then the two fractions are equal as well.

One way to find a common denominator is to check to see if one denominator is a factor of the other denominator. If so, the greater denominator can be used as the common denominator.

Example

Problem

Are `2/6` and `8/18` equivalent fractions?

 

Does `2/6=8/18`?

To solve this problem, find a common denominator for the two fractions. This will help you compare the two fractions.

 

Since `6` is a factor of `18`, you can write both fractions with `18` as the denominator.

 

`(2*3)/(6*3)=6/18`

Start with the fraction `2/6`.

Multiply the denominator, `6`, by `3` to get a new denominator of `18`. Since you multiply the denominator by `3`, you must also multiply the numerator by `3`.

 

`8/18`

The fraction `8/18` already has a denominator of `18`, so you can leave it as is.

 

`6/18` does not equal `8/18`

 

 

Compare the fractions. Now that both fractions have the same denominator, `18`, you can compare numerators.

Answer

`2/6` and `8/18` are not equivalent fractions.

When one denominator is not a factor of the other denominator, you can find a common denominator by multiplying the denominators together.

Example

Problem

 

Determine whether `3/6` and `5/10` are equivalent fractions.

 

`6 * 10 = 60`

Use `60` as a common denominator.

 

`3/6=(3*10)/(6*10)=30/60`

Multiply the numerator and denominator of `3/6` by `10` to get `60` in the denominator.

 

`5/10=(5*6)/(10*6)=30/60`

Multiply the numerator and denominator of `5/10` by `6`.

 

`30/60=30/60`

Now that the denominators are the same, compare the numerators.

Answer

Yes, `3/6` and `5/10` are equivalent fractions.

Since `30` is the value of the numerator for both fractions, the two fractions are equal.

Notice in the above example that you can use `30` as the least common denominator since both `6` and `10` are factors of `30`. Any common denominator will work.

In some cases, you can simplify one or both of the fractions, which can result in a common denominator.

Example

Problem

 

Determine whether `2/3` and `40/60` are equivalent fractions.

 

 

 

 

`40/60=(40-:10)/(60-:10)=4/6`

Simplify `40/60`. Divide the numerator and denominator by the common factor `10`.

 

 

`4/6=(4-:2)/(6-:2)=2/3`

`4/6` is still not in lowest terms, so divide the numerator and the denominator again, this time by the common factor `2`.

 

`2/3=2/3`

Compare the fractions. The numerators and denominators are the same.

Answer   Yes, `2/3` and `40/60` are equivalent fractions.

Note: In the example above, you could have used the common factor of `20` to simplify `40/60` directly to `2/3`.

Determining Equivalent Fractions

 

To determine whether or not two fractions are equivalent:

 

Step `1`: Rewrite one or both of the fractions so that they have common denominators.

 

Step `2`: Compare the numerators to see if they have the same value. If so, then the fractions are equivalent.

 

 

Which of the following fraction pairs are equivalent?

 

A) `5/7 and 7/5`

 

B) `12/30 and 6/10`

 

C) `4/20 and 1/5`

 

D) `8/11 and 8/22`

 

+ 

Show/Hide Answer

 

Comparing Fractions Using `<` and `>`

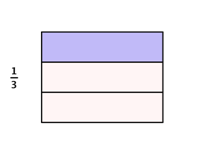
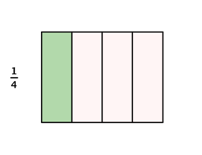
When given two or more fractions, it is often useful to know which fraction is greater than or less than the other. For example, if the discount in one store is `1/3` off the original price and the discount in another store is `1/4` off the original price, which store is offering a better deal? To answer this question, and others like it, you can compare fractions.

The image shows a grid that 1 column and 3 rows where blocks are divided equally horizontally. 1 of the blocks is shaded. The image is labeled one over three, or one-third.The image shows a grid that has 4 columns and 1 row where blocks are divided equally vertically. 1 of the blocks is shaded. It is labeled one over four, or one-fourth.

To determine which fraction is greater, you need to find a common denominator. You can then compare the fractions directly. Since `3` and `4` are both factors of `12`, you will divide the whole into `12` parts, create equivalent fractions for `1/3` and `1/4`, and then compare.

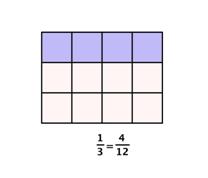
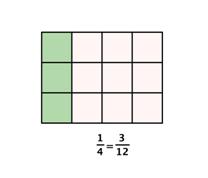
The image shows a grid that has 4 columns and 3 rows where squares are divided into 12 equal parts. 4 of the squares are shaded. The image is labeled one-third equals four-twelfths.The image shows a grid that has 4 columns and 3 rows where squares are divided into 12 equal parts. 3 of the squares are shaded. It is labeled one-fourth equals three-twelfths.

Now you see that `1/3` contains `4` parts of `12`, and `1/4` contains `3` parts of `12`. So, `1/3` is greater than `1/4`.

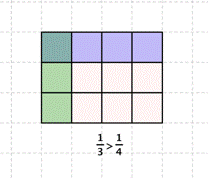
The image shows a grid that has 4 columns and 3 rows where squares are divided into 12 equal parts. The 3 squares in the first column are shaded green, representing one fourth of the total squares. The 4 squares in the first row are shaded purple, representing one third of the total squares. The square in the upper left corner is part of both the vertical shaded column and the horizontal shaded row. The grid is labeled one-third is greater than one-fourth.

As long as the denominators are the same, the fraction with the greater numerator is the greater fraction, as it contains more parts of the whole. The fraction with the lesser numerator is the lesser fraction, as it contains fewer parts of the whole.

Recall that the symbol `<` means “less than”, and the symbol `>` means “greater than”. These symbols are inequality symbols. So, the true statement `3<8` is read as “`3` is less than `8`” and the statement `5>3` is read as “`5` is greater than `3`”. One way to help you remember the distinction between the two symbols is to think that the smaller end of the symbol points to the lesser number.

As with comparing whole numbers, the inequality symbols are used to show when one fraction is “greater than” or “less than” another fraction.

Comparing Fractions

 

To compare two fractions:

 

Step `1`: Compare denominators. If they are different, rewrite one or both fractions with a common denominator.

 

Step `2`: Check the numerators. If the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. And, as noted above, if the numerators are equal, the fractions are equivalent.

 

 

Example

Problem

Use `<` or `>` to compare the two fractions `4/5` and `14/20`.

 

Is `4/5>14/20` or is `4/5<14/20`?

You cannot compare the fractions directly because they have different denominators. You need to find a common denominator for the two fractions.

 

`4/5=text()?/20`

Since `5` is a factor of `20`, you can use `20` as the common denominator.

 

`(4*4)/(5*4)=16/20`

Multiply the numerator and denominator by `4` to create an equivalent fraction with a denominator of `20`.

 

`16/20>14/20`  

 

Compare the two fractions. `16/20` is greater than `14/20`. 

Answer

`4/5>14/20`

If `16/20>14/20`, then `4/5>14/20`, since `4/5=16/20`. 

 

Which of the following is a true statement?

 

A) `5/6<24/30`

 

B) `75/100>9/12`

 

C) `4/16>1/3`

 

D) `3/8<20/40`

 

+ 

Show/Hide Answer

 

Summary

You can compare two fractions with like denominators by comparing their numerators. The fraction with the greater numerator is the greater fraction, as it contains more parts of the whole. The fraction with the lesser numerator is the lesser fraction as it contains fewer parts of the whole. If two fractions have the same denominator, then equal numerators indicate equivalent fractions.