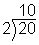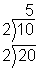Factors and Primes
Learning Objectives
- Recognize (by using the divisibility rule) if a number is divisible by `2, 3, 4, 5, 6, 9, text(or ) 10`.
- Find the factors of a number.
- Determine whether a number is prime, composite, or neither.
- Find the prime factorization of a number.
Introduction
Natural numbersThe numbers `1`, `2`, `3`, `4` and so on. Also called counting numbers., also called counting numbers (`1, 2, 3,` and so on), can be expressed as a product of their factors A number that is multiplied by another number or numbers to get a product. For example, in the equation `4 * 5 = 20`, `4` and `5` are factors. . When working with a fraction, you often need to make the fraction as simple as possible. This means that the numeratorThe top number of a fraction that tells how many parts of a whole are being represented. and the denominatorThe bottom number of a fraction that tells how many equal parts are in the whole. have no common factors other than `1`. It will help to find factors, so that later you can simplify and compare fractions.
When a natural number is expressed as a product of two other natural numbers, those other numbers are factors of the original number. For example, two factors of `12` are `3` and `4`, because `3 * 4 = 12`.
When one number can be divided by another number with no remainder, we say the first number is divisible Can be divided by a number without leaving a remainder. For example, `20` is divisible by `4` because `20` ÷ `4 = 5` (no remainder). by the other number. For example, `20` is divisible by `4` (`20-:4=5`). If a number is divisible by another number, it is also a multipleAny number that has a given number as a factor. For example, `4`, `8`, `16`, and `200` are multiples of `4`, because `4` is a factor of each of these numbers. of that number. For example, `20` is divisible by `4`, so `20` is a multiple of `4`.
Divisibility testsA rule that tells quickly whether dividing a number by another number can be done without leaving a remainder. are rules that let you quickly tell if one number is divisible by another. There are many divisibility tests. Here are some of the most useful and easy to remember:
- A number is divisible by `2` if the last (ones) digit is divisible by `2`. That is, the last digit is `0, 2, 4, 6`, or `8`. (We then say the number is an even numberA whole number that is divisible by `2`..) For example, in the number `236`, the last digit is `6`. Since `6` is divisible by `2` (`6-:2=3`), `236` is divisible by `2`.
- A number is divisible by `3` if the sum of all the digits is divisible by `3`. For example, the sum of the digits of `411` is `4 + 1 + 1 = 6`. Since `6` is divisible by `3` (`6-:3=2`), `411` is divisible by `3`.
- A number is divisible by `5` if the last digit is `0` or `5`. For example, `275` and `1,340` are divisible by `5` because the last digits are `5` and `0`.
- A number is divisible by `10` if the last digit is `0`. For example, `520` is divisible by `10` (last digit is `0`).
|
Other useful divisibility tests:
`1`: A number is divisible by `4` if the last two digits are divisible by `4`.
`2`: A number is divisible by `6` if it is divisible by both `2` and `3`.
`3`: A number is divisible by `9` if the sum of its digits is divisible by `9`.
|
Here is a summary of the most commonly used divisibility rules.
|
A number is divisible by
|
Example
|
|
`2` if the last digit is even (`0, 2, 4, 6, 8`).
|
`426` yes
`273` no
|
|
`3` if the sum of the digits is divisible by `3`.
|
`642` yes
(`6+4+2=12`, `12` is divisible by `3`)
`721` no
(`7+2+1=10`, `10` is not divisible by `3`)
|
|
`4` if the last two digits form a number that is divisible by `4`.
|
`164` yes
(`64` is divisible by `4`)
`135` no
(`35` is not divisible by `4`)
|
|
`5` if the last digit is `0` or `5`.
|
`685` yes
`432` no
|
|
`6` if the number is divisible by `2` and `3`.
|
`324` yes
(it is even and `3+2+4=9`)
`411` no
(although divisible by `3`, it is not even)
|
|
`9` if the sum of the digits is divisible by `9`.
|
`279` yes
(`2+7+9=18`)
`512` no
(`5 + 1 + 2=8`)
|
|
`10` if the last digit is a `0`.
|
`620` yes
`238` no
|
If you need to check for divisibility of a number without a rule, divide (either using a calculator or by hand). If the result is a number without any fractional part or remainder, then the number is divisible by the divisorThe number that is being divided into the dividend in a division problem. In the problem `8 ÷ 2 = 4`, `2` is the divisor. . If you forget a rule, you can also use this strategy.
|
Determine whether `522` is divisible by `2, 3, 4, 5, 6, 9`, or `10`.
A) `2` and `3` only
B) `4` only
C) `2, 3, 6`, and `9` only
D) `4, 5`, and `10` only
A) `2` and `3` only
Incorrect. Although `522` is divisible by `2` (the last digit is even) and `3` (`5+2+2=9`, which is a multiple of `3`), it is also divisible by `6` and `9`. The correct answer is `2,3, 6`, and `9` only.
B) `4` only
Incorrect. The last two digits (`22`) are not divisible by `4`, so `522` is not divisible by `4`. `522` has a last digit divisible by `2`, so `522` is divisible by `2`. The sum of the digits is divisible by `3` (`5+2+2=9`) and by `9`, so `522` is divisible by `3` and `9`. Since `522` is divisible by `2` and `3`, it is divisible by `6`. Since the last digit is not `0` or `5`, `522` is not divisible by `5` or `10`. The correct answer is `2, 3, 6`, and `9` only.
C) `2, 3, 6`, and `9` only
Correct. `522` is divisible by `2` (the last digit is even) and `3` (`5+2+2=9`, which is a multiple of `3`). Since it is divisible by `2` and `3`, it is also divisible by `6`. Also, the sum of the digits is divisible by `9`, so `522` is divisible by `9`. Since the last digit is not `0` or `5`, `522` is not divisible by `5` or `10`. The number formed by the last two digits, `22`, is not divisible by `4`, so `522` is not divisible by `4`.
D) `4, 5`, and `10` only
Incorrect. The last two digits are not divisible by `4`, so `522` is not divisible by `4`. The last digit is not `0` or `5` so `522` is not divisible by `5`. The last digit is not `0`, so `522` is not divisible by `10`. However, `522` is divisible by `2` (the last digit is even) and `3` (`5+2+2=9`, which is a multiple of `3`). Since it is divisible by `2` and `3`, it is also divisible by `6`. Also, the sum of the digits is divisible by `9`, so `522` is divisible by `9`. The correct answer is `2, 3, 6`, and `9` only.
|
To find all the factors of a number, you need to find all numbers that can divide into the original number without a remainder. The divisibility rules from above will be extremely useful!
Suppose you need to find the factors of `30`. Since `30` is a number you are familiar with, and small enough, you should know many of the factors without applying any rules. You can start by listing the factors as they come to mind:
`2 * 15`
`3 * 10`
`5 * 6`
Is that it? Not quite. All natural numbers except `1` also have `1` and the number itself as factors:
`1 * 30`
The factors of `30` are `1, 2, 3, 5, 6, 10, 15`, and `30`.
When you find one factor of a number, you can easily find another factor: it is the quotient using that first factor as the divisor. For example, once you know `2` is a factor of `30`, then `30-:2` is another factor. A pair of factors whose product is a given number is a factor pairA pair of numbers whose product is a given number. For example, `2` and `15` are a factor pair of `30` because `2*15 = 30`. Both `2` and `15` are factors of `30`. of the original number. So, `2` and `15` are a factor pair for `30`.
What do you do if you need to factor a greater number and you can’t easily see its factors? That’s where the divisibility rules will come in quite handy. Here is a general set of steps that you may follow:
- Begin with `1` and check the numbers sequentially, using divisibility rules or division.
- When you find a factor, find the other number in the factor pair.
- Keep checking sequentially, until you reach the second number in the last factor pair you found, or until the result of dividing gives a number less than the divisor.
Note that you can stop checking when the result of dividing is less than the number you’re checking. This means that you have already found all factor pairs, and continuing the process would find pairs that have been previously found.
If a number has exactly two factors, `1` and itself, the number is a prime numberA natural number with exactly two factors: `1` and the number itself.. A number that has more factors than itself and `1` is called a composite numberA natural number that has at least one factor other than `1` and itself.. The number `1` is considered neither prime nor composite, as its only factor is `1`. To determine whether a number is prime, composite, or neither, check factors. Here are some examples.
|
Number
|
Composite, Prime, or Neither?
|
Explanation
|
|
`1`
|
Neither
|
`1` does not have two different factors, so it is not prime.
|
|
`2`
|
Prime
|
`2` has only the factors `2` and `1`.
|
|
`3`
|
Prime
|
`3` has only the factors `3` and `1`.
|
|
`4`
|
Composite
|
`4` has more than two factors: `1`, `2`, and `4`, so it is composite.
|
|
`5, 7, 11, 13`
|
Prime
|
Each number has only two factors: `1` and itself.
|
|
`6, 8, 9, 10, 50, 63`
|
Composite
|
Each number has more than two factors.
|
|
Find all the factors of `48`.
`1, 2, 3, 4, 6, 8, 12, 16, 24, 48`
|
A composite number written as a product of only prime numbers is called the prime factorizationA number written as the product of its prime factors. of the number. One way to find the prime factorization of a number is to begin with the prime numbers `2, 3, 5, 7, 11` and so on, and determine whether the number is divisible by the primes.
For example, if you want to find the prime factorization of `20`, start by checking if `20` is divisible by `2`. Yes, `2 * 10 = 20`.
Then factor `10`, which is also divisible by `2` (`2 * 5 = 10`).
Both of those factors are prime, so you can stop. The prime factorization of `20` is `2 * 2 * 5`, which you can write using exponential notation A notation that represents repeated multiplication using a base and an exponent. For example, `2^4` is notation that means `2 * 2 * 2 * 2`. This notation tells you that `2` is used as a factor `4` times. `2^4=16`. (Also called exponential form.) as `2^2 * 5`.
One way to find the prime factorization of a number is to use successive divisions.
|
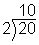
|
Divide `20` by `2` to get `10`. `2` is being used because it is a prime number and a factor of `20`. You could also have started with `5`.
|
|
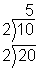
|
Then divide `10` by `2` to get `5`.
|
|
`2*2*5`
|
Multiplying these divisors forms the prime factorization of `20`.
|
To help you organize the factoring process, you can create a factor treeA diagram showing how a number can be written as factors, and those factors written as a product of factors, and so on until only prime numbers are used.. This is a diagram that shows a factor pair for a composite number. Then, each factor that isn’t prime is also shown as a factor pair. You can continue showing factor pairs for composite factors, until you have only prime factors. When a prime number is found as a factor, circle it so you can find it more easily later.
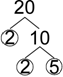
Written using exponential notation, the prime factorization of `20` is again `2^2 * 5`.
Notice that you don’t have to start checking the number using divisibility of prime numbers. You can factor `20` to `4 * 5`, and then factor `4` to `2 * 2`, giving the same prime factorization: `2 * 2 * 5`.
Now look at a more complicated factorization.
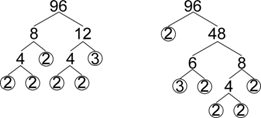
Notice that there are two different trees, but they both produce the same result: five `2`s and one `3`. Every number will only have one, unique prime factorization. You can use any sets of factor pairs you wish, as long as you keep factoring composite numbers.
When you rewrite the prime factorization of `96` (`2*2*2*2*2*3`) in exponential notation, the five `2`s can be written as `2^5`. So, `96 = 2^5 * 3`.
|
When finding the prime factorization of `72`, Marie began a tree diagram using the two factors `9` and `8`. Which of the following statements are true?
`1`. Marie started the diagram incorrectly and should have started the tree diagram using the factors `2` and `36`.
`2`. Marie’s next set of factor pairs could be `3`, `3` and `2`, `4`.
`3`. Marie’s next set of factor pairs could be `3`, `3` and `9`, `8`.
`4`. Marie didn’t have to use a tree diagram.
A) `1` only
B) `2` only
C) `3` and `4` only
D) `2` and `4` only
A) `1` only
Incorrect. Marie could have started her tree diagram with the factors `2` and `36`, but she does not have to start with those factors. Starting with `9` and `8` is fine. The correct answer is D.
B) `2` only
Incorrect. Yes, Marie’s next set of factor pairs could contain `3`, `3`, and `2`, `4`, but statement `4` is also correct. The correct answer is D.
C) `3` and `4` only
Incorrect. Statement `4` is correct: Marie does not have to use a tree diagram, but `3` is not true. When creating a prime factorization, the factors are not combined with the previous composite. The correct answer is D.
D) `2` and `4` only
Correct. Marie’s next set of factor pairs could read `3`, `3`, and `2`, `4`, as `3*3` is a factorization of `9` and `2*4` is a factorization of `8`. Marie could also find the prime factorization by using successive divisions.
|
Summary
Finding the factors of a natural number means that you find all the possible numbers that will divide into the given number without a remainder. There are many rules of divisibility to help you to find factors more quickly. A prime number is a number that has exactly two factors. A composite number is a number that has more than two factors. The prime factorization of a number is the product of the number’s prime factors.