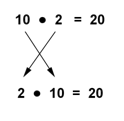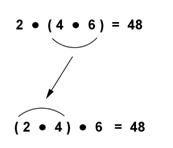Properties and Laws of Whole Numbers
Mathematics often involves simplifying numerical expressions. When doing so, you can use laws and properties that apply to particular operations. The multiplication property of `1` states that any number multiplied by `1` equals the same number, and the addition property of zero states that any number added to zero is the same number.
Two important laws are the commutative laws, which state that the order in which you add two numbers or multiply two numbers does not affect the answer. You can remember this because if you commute to work you go the same distance driving to work and driving home as you do driving home and driving to work. You can move numbers around in addition and multiplication expressions because the order in these expressions does not matter.
You will also learn how to simplify addition and multiplication expressions using the associative laws. As with the commutative laws, there are associative laws for addition and multiplication. Just like people may associate with people in different groups, a number may associate with other numbers in one group or another. The associative laws allow you to place numbers in different groups using parentheses.
The addition property of 0The sum of any number and `0` is equal to that number. The number `0` is often called the additive identity. states that for any number being added to `0`, the sum equals that number. Remember that you do not end up with zero as an answer; that only happens when you multiply. Your answer is simply the same as your original number.
|
Example |
||
|
Problem |
`62 + 0=?` |
|
|
`62 + 0 = 62` |
Adding zero to `62` does not add any quantity to the sum, so the number remains `62`. |
|
|
Answer `62 + 0 = 62` |
||
|
`112 + 0=?`
A) `112`
B) `0`
C) `1`
D) `1,120`
|
According to the multiplication property of 1The product of any number and `1` is equal to that number. The number `1` is often called the multiplicative identity., the product of `1` and any number results in that number. The answer is simply identical to the original number.
|
Example |
||
|
Problem |
`2,500*1=?` |
|
|
`2,500*1 = 2,500` |
Multiplying `2,500` by `1` yields the same number. |
|
|
Answer `2,500 * 1=2,500` |
||
|
`72,540 *1=text(?)`
A) `725,401`
B) `72,541`
C) `72,540`
D) `72,539`
|
The commutative law of additionTwo numbers can be added in any order without changing the sum. For example: `6 + 4 = 4 + 6` states that you can change the position of numbers in an addition expression without changing the sum. For example, `3 + 2` is the same as `2 + 3`.
`3 + 2 = 5`
`2 + 3 = 5`
You likely encounter daily routines in which the order can be switched. For example, when you get ready for work in the morning, putting on your left glove and right glove is commutative. You could put the right glove on before the left glove, or the left glove on before the right glove. Likewise, brushing your teeth and combing your hair is commutative, because it does not matter which one you do first.
Remember that this law only applies to addition, and not subtraction. For example:
`8 - 2` is not the same as `2 - 8`.
Below, you will find examples of expressions that have been changed with the commutative law. Note that expressions involving subtraction cannot be changed.
|
Original Expression |
Rewritten Expression |
|
`4 + 5` |
`5 + 4` |
|
`6 + 728` |
`728 + 6` |
|
`9 + 4 + 1` |
`9 + 1 + 4` |
|
`9 - 1` |
cannot be changed |
|
`72 - 10` |
cannot be changed |
|
`128 - 100` |
cannot be changed |
You also will likely encounter real life routines that are not commutative. When preparing to go to work, putting on our clothes has to occur before putting on a coat. Likewise, getting in the car has to occur before putting the key in the ignition. In a store, you would need to pick up the items you are buying before proceeding to the cash register for checkout.
|
Example |
||
|
Problem
|
Write the expression `10 + 25` in a different way, using the commutative law of addition, and show that both expressions result in the same answer. |
|
|
`10 + 25 = 35` |
Solving the problem yields an answer of `35`. |
|
|
`25 + 10` |
Using the commutative property, you can switch the `10` and the `25` so that they are in different positions. |
|
|
`25 + 10 = 35` |
Adding `25` to `10` in this new order also yields `35`. |
|
|
Answer `10 + 25 = 35` and `25 + 10 = 35` |
||
|
Rewrite `15 + 12 = 27` in a different way, using the commutative law of addition.
A) `15 = 12 + 27`
B) `12 = 15 + 27`
C) `15 + (12 = 27)`
D) `12 + 15 = 27`
|
Multiplication also has a commutative law. The commutative law of multiplication Two numbers can be multiplied in any order without changing the product. For example, `8 * 9 = 9 * 8`. states that when two or more numbers are being multiplied, their order can be changed without affecting the answer. In the example below, note that `5` multiplied by `4` yields the same result as `4` multiplied by `5`. In both cases, the answer is `20`.
`5 * 4 = 20`
`4 * 5 = 20`
This example shows how numbers can be switched in a multiplication expression.
|
Example |
||
|
Problem
|
Write the expression `30*50` in a different way, using the commutative law of multiplication, and show that both expressions result in the same answer. |
|
|
`30 * 50 = 1,500` |
Solving the problem yields an answer of `1,500`. |
|
|
`50 * 30` |
Using the commutative law, you can switch the `30` and the `50` so that they are in different positions. |
|
|
`50 * 30 = 1,500` |
Multiplying `50` and `30` also yields `1,500`. |
|
|
Answer `50 * 30` and `30 * 50 = 1,500` |
||
Keep in mind that when you are using the commutative law, only the order is affected. The grouping remains unchanged.
|
Problem: Rewrite `52 * 46` in a different way, using the commutative law of multiplication.
A) `42 * 56`
B) `5 * 246`
C) `5 * 24 * 6`
D) `46 * 52`
|
Below are two ways of simplifying and solving an addition problem. Note that you can add numbers in any order. In the first example, `4` is added to `5` to make `9`.
`4 + 5 + 6 = 9 + 6 = 15`
Here, the same problem is solved, but this time, `5` is added to `6` to make `11`. Note that solving it this way yields the same answer.
`4 + 5 + 6 = 4 + 11 = 15`
The associative law of additionFor three or more numbers, the sum is the same regardless of how you group the numbers. For example, `(6 + 2) + 1 = 6 + (2 + 1)`. states that numbers in an addition expression can be regrouped using parentheses. You can remember the meaning of the associative law by remembering that when you associate with family members, friends, and co-workers, you end up forming groups with them. In the following expression, parentheses are used to group numbers together so that you know what to add first. Note that when parentheses are present, any numbers within parentheses are numbers you will add first. The expression can be re-written with different groups using the associative law.
`(4 + 5) + 6 = 9 + 6 = 15`
`4 + (5 + 6) = 4 + 11 = 15`
Here, it is clear that the parentheses do not affect the final answer. The answer is the same regardless of where the parentheses are.
|
Example |
||
|
Problem
|
Rewrite `(5 + 8) + 3` using the associative law of addition. Show that the rewritten expression yields the same answer. |
|
|
`(5 + 8) + 3 = 13 + 3 = 16` |
The original expression yields an answer of `16`. |
|
|
`5 + (8 + 3) = 5 + 11 = 16` |
Grouping `8` and `3` instead of `5` and `8` results in the same answer of `16`. |
|
|
Answer `(5 + 8) + 3 = 16` and `5 + (8 + 3) = 16` |
||
When rewriting an expression using the associative law, remember that you are regrouping the numbers and not reversing the order, as in the commutative law.
|
Rewrite `10 + (5 + 6)` using the associative property.
A) `(5 + 6) + 10`
B) `10 + (6 + 5)`
C) `(10 + 5) + 6`
D) `(10 + 6) + 5`
|
Multiplication has an associative law that works exactly the same as the one for addition. The associative law of multiplication For three or more numbers, the product is the same regardless of how you group the numbers. For example, `(3 * 5) * 7 = 3 * (5 * 7)`. states that numbers in a multiplication expression can be regrouped using parentheses. The following expression can be rewritten in a different way using the associative law.
`(2 * 3) * 4 = 2 * (3 * 4)`
Here, it is clear that the parentheses do not affect the final answer. The answer is the same regardless of where the parentheses are.
|
Example |
||
|
Problem
|
Rewrite `(10*200)*24` using the associative law of multiplication, and show that the rewritten expression yields the same answer. |
|
|
`(10 * 200) * 24 = 2000 * 24 = 48,000` |
The original expression yields an answer of `48,000`. |
|
|
`10 * (200 * 24) = 10 * 4800 = 48,000`
|
Grouping `200` and `24` instead of `10` and `200` results in the same answer of `48,000`. |
|
|
Answer `(10 * 200) * 24 = 48,000` and `10*(200*24)=48,000` |
||
When rewriting an expression using the associative law, remember that you are regrouping the numbers and not changing the order. Changing the order uses the commutative law.
|
Rewrite `8 * (7 * 6)` using the associative property.
A) `(8 * 7) * 6`
B) `(7 * 6) * 8`
C) `(7 * 8) * 6`
D) `(8 * 76)`
|
When an expression is being rewritten, you can tell whether it is being rewritten using the commutative or associative laws based on whether the order of the numbers change or the numbers are being regrouped using parentheses.
If an expression is rewritten so that the order of the numbers is changed, the commutative law is being used.
|
Example |
||
|
Problem
|
`10*2=20` is rewritten as `2*10=20`. Was this expression rewritten using the commutative law or the associative law? |
|
|
|
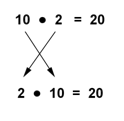
Rewriting the expression involves switching the order of the numbers. Therefore, the commutative law is being used. |
|
|
Answer The commutative law is being used to rewrite the expression. |
||
Remember that when you associate with friends and family, typically you are grouping yourself with other people. So, if numbers in an expression are regrouped using parentheses and the order of numbers remains the same, then the associative law is being used.
|
Example |
||
|
Problem
|
`2*(4*6)=48` is rewritten as `(2*4)*6=48`. Was this expression rewritten using the commutative law or the associative law? |
|
|
|
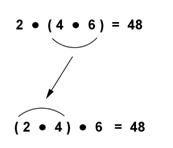
Regrouping using parentheses does not change the order of the numbers. Therefore, the associative law is being used. |
|
|
Answer The associative law is being used to rewrite the expression. |
||
|
`12 * (6 * 2) = 144` is rewritten as `(12 * 6) * 2 = 144`. Was this expression rewritten using the commutative law or the associative law?
A) commutative law
B) associative law
|
If there are absolutely no parentheses in a problem that is being rewritten, you can assume the associative law is not being used.
|
`17 * 3 = 51` is rewritten as `3 * 17 = 51`. Was this expression rewritten using the commutative law or associative law?
A) commutative law
B) associative law
|
The associative and commutative laws are useful when you have an expression with only addition. Using the commutative law, the numbers can be reordered so that the numbers that are easiest to add are next to each other, and using the associative law, you can group them in any way.
For example, here are some of the ways we can add `6 + 5 + 4` using the associative and commutative laws. Note that the answer is always the same.
`(6 + 5) + 4 = 11 + 4 = 15` (grouping `6` and `5` to add first)
`(5 + 6) + 4 = 11 + 4 = 15` (reordering `6` and `5`)
`5 + (6 + 4) = 5 + 10 = 15` (grouping `6` and `4` to add first)
`6 + (5 + 4) = 6 + 9 = 15` (grouping `5` and `4` to add first)
`6 + (4 + 5) = 6 + 9 = 15` (reordering `4` and `5`)
`(6 + 4) + 5 = 10 + 5 = 15` (grouping `6` and `4` to add first)
|
Example |
||
|
Problem
|
Write the expression `13 + 28 + 7` a different way to make it easier to simplify. Then simplify. |
|
|
`13 + 28 + 7`
`13 + 7 + 28` |
Using the commutative property, reorder the numbers `7` and `28` since `13 + 7` is easier to add than `13+28`. |
|
|
`20 + 28` |
Using the associative property, group the `13` and `7` together and add them first. |
|
|
`48` |
Add `20` and `28`. |
|
|
Answer `13 + 28 + 7 = 13 + 7 + 28 = 48` |
||
Sometimes the commutative and associative laws can make the problem easy enough to do in your head.
|
Example |
||
|
Problem
|
Jim is buying `8` pears, `7` apples, and `2` oranges. He decided the total number of fruits is `8 + 7 + 2`. Use the commutative property to write this expression in a different way. Then find the total. |
|
|
`8 + 7 + 2` `8 + 2 + 7` |
Using the commutative property, reorder `2` and `7`. |
|
|
`10 + 7` |
Using the associative property, group the `8` and `2` together and add them first. |
|
|
`17` |
Add `10` and `7`. |
|
|
Answer `8 + 7 + 2 = 8 + 2 + 7 = 17` |
||
This also works when you are multiplying more than two numbers. You can use the commutative and associative laws freely if the expression involves only multiplication.
|
Example |
||
|
Problem
|
There are `2` trucks in a garage, and each truck holds `60` boxes. There are `5` laptop computers in each box. Find the number of computers in the garage. |
|
|
`2 * 60 * 5` |
In order to find the answer, you need to multiply the number of trucks times the number of boxes in each truck, and, then by the number of computers in each box. |
|
|
`2 * 5 * 60` |
Using the commutative property, reorder the `5` and the `60`. Now you can multiply `2*5` first. |
|
|
`10 * 60` |
Using the associative property, multiply the `2` and the `5`, `2 * 5 = 10`. |
|
|
`600` |
Now it's easier to multiply `10` and `60` to get `600`. |
|
|
Answer There are `600` computers in the garage. |
||
The addition property of `0` states that for any number being added to zero, the sum is the same number. The multiplication property of `1` states that for any number multiplied by one, that answer is that same number. Zero is called the additive identity, and one is called the multiplicative identity.
When you rewrite an expression by a commutative law, you change the order of the numbers being added or multiplied. When you rewrite an expression using an associative law, you group a different pair of numbers together using parentheses.
You can use the commutative and associative laws to regroup and reorder any number in an expression that involves only addition. You can also use the commutative and associative laws to regroup and reorder any number in an expression that involves only multiplication.
