Dividing Whole Numbers and Applications

Learning Objectives

Introduction

Some people think about division as “fair sharing” because when you divide a number you are trying to create equal parts. Division is also the inverse operationA mathematical operation that can reverse or “undo” another operation. Addition and subtraction are inverse operations. Multiplication and division are inverse operations. of multiplication because it “undoes” multiplication. In multiplication, you combine equal sets to create a total. In division, you separate a whole group into sets that have the same amount. For example, you could use division to determine how to share `40` empanadas among `12` guests at a party.

What is Division?

Division is splitting into equal parts or groups. For example, one might use division to determine how to share a plate of cookies evenly among a group. If there are `15` cookies to be shared among five people, you could divide `15` by `5` to find the “fair share” that each person would get. Consider the picture below.

The picture shows five plates with three cookies on each plate.

`15` cookies split evenly across `5` plates results in `3` cookies on each plate. You could represent this situation with the equation:

`15-:5 = 3`

You could also use a number line to model this division. Just as you can think of multiplication as repeated addition, you can think of division as repeated subtraction. Consider how many jumps you take by `5`s as you move from `15` back to `0` on the number line.

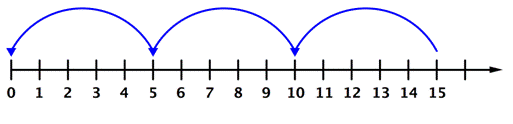
The image shows a number line that goes from 0 to 15 with 14 marks in between. A curved line above the number line shows 3 jumps going backwards from 15 to 10, from 10 to 5, from 5 to 0.

Notice that there are `3` jumps that you make when you skip count by `5` from `15` back to `0` on the number line. This is like subtracting `5` from `15` three times. This repeated subtraction can be represented by the equation: `15-:5 = 3`.

Finally, consider how an area model can show this division. Ask yourself, if you were to make a rectangle that contained `15` squares with `5` squares in a row, how many rows would there be in the rectangle? Start by making one row of `5` squares:

 

 

`5`

 

 

 

 

 

 

 

 

 

Then add two more rows of 5 squares so you have `15` squares.

 

 

 

`5`

 

 

 

 

 

 

 

 

`3`

 

 

 

 

 

 

 

 

 

 

 

 

 

 

The number of rows is `3`. So, `15` divided by `5` is equal to `3`.

Example

Problem

Find `24-:3`  using a set model and a number line model.

 

 

 

Set Model:

The image shows a set model with 24 scattered dots separated by two angular lines making 3 sections with 8 dots in each section.

 

Number line model:

The image shows number line that goes from 0 to 24 with 23 marks in between. A curved line above the number line shows 8 jumps going backwards from 24 to 21, from 21 to 18, from 18 to 15, from 15 to 12, from 12 to 9, from 9 to 6, from 6 to 3, and from 3 to 0.

 

 

Answer

`24-:3=8`

 

 

Ways to Represent Division

As with multiplication, division can be written using a few different symbols. We showed this division written as `15-:5=3`, but it can also be written two other ways:

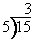
The image shows a long division problem. The dividend is 15, the divisor is 5, and the quotient is 3.

`15/5=3`

Each part of a division problem has a name. The number that is being divided up, that is the total, is called the dividend The number to be divided up in a division problem. In the problem `8` ÷ `2 = 4`, `8` is the dividend. . In the work in this topic, this number will be the larger number, but that is not always true in mathematics. The number that is dividing the dividend is called the divisor The number that is being divided into the dividend in a division problem. In the problem `8` ÷ `2 = 4`, `2` is the divisor. . The answer to a division problem is called the quotient The result of a division problem. In the problem `8` ÷ `2 = 4`, `4` is the quotient. .

The blue box below summarizes the terminology and common ways to represent division.

 

Three Ways to Represent Division

 

`12-:3=4` (with a division symbol; this equation is read “`12` divided by `3` equals `4`.”)

 

The image shows a long division problem. The dividend is 12, the divisor is 3, and the quotient is 4. (with a division or long division symbol; this expression is read “`12` divided by `3` equals `4`.” Notice here, though, that you have to start with what is underneath the symbol. This may take some getting used to since you are reading from right to left and bottom to top!)

 

`12/3=4` (with a fraction bar; this expression can also be read “`12` divided by `3` equals `4`.” In this format, you read from top to bottom.)

 

In the examples above, `12` is the dividend, `3` is the divisor and `4` is the quotient.

 

`text(Dividend)-:text(Divisor)=text(Quotient)`

 

The image shows a long division symbol with the word Dividend inside the symbol, the word Divisor to the left of the symbol, and the word Quotient above the symbol.

 

`text(Dividend)/text(Divisor)=text(Quotient`

 

 

Which of the following expressions represent dividing `$56` equally among `7` people?

`#1`

`7/56`

 

`#2`

`56-:7`

 

`#3`

The image shows a long division problem. The dividend is 7 and the divisor is 56.

 

A) `#2` represents the situation.

 

B) All three expressions represent the situation.

 

C) `#1` represents the situation.

 

D) `#3` represents the situation.

 

+ 

Show/Hide Answer

 

Dividing Whole Numbers

Once you understand how division is written, you are on your way to solving simple division problems. You will need your multiplication facts to perform division. If you do not have them memorized, you can guess and check or use a calculator.

Consider the following problems:

`10-:5=?`

`48-:2=?`

`30-:5=?`

In the first problem, `10-:5`, you could ask yourself, “how many fives are there in ten?” You can probably answer this easily. Another way to think of this is to consider breaking up `10` into `5` groups and picturing how many would be in each group.

`10-:5 = 2`

To solve `48-:2`, you might realize that dividing by `2` is like splitting into two groups or splitting the total in half. What number could you double to get `48`?

`48-:2=24`

To figure out `30-:5`, you could ask yourself, how many times do you have to skip count by `5` to get from `0` to `30`? `5, 10, 15, 20, 25, 30`. You have to skip count `6` times to get to `30`.

`30-:5=6`

Compute `35-:5`. 

 

+ 

Show/Hide Answer

 

 

Compute `32-:4`. 

 

+ 

Show/Hide Answer

 

Sometimes when you are dividing, you cannot easily share the number equally. Think about the division problem `9-:2`. You could think of this problem as `9` pieces of chocolate being split between `2` people. You could make two groups of `4` chocolates, and you would have one chocolate left over.

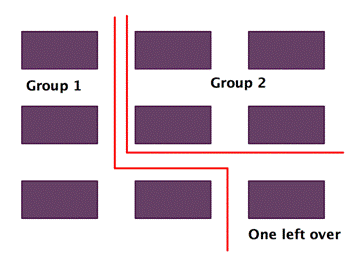
The image shows pieces of chocolate lined up in 3 rows of 3. Two angular lines divide the chocolates into 2 groups with 4 chocolates in each group. One is left over.

In mathematics, this left over part is called the remainder The amount left over after dividing a number. In the problem `11` ÷ `4 = 2` R`3`, `3` is the remainder. . It is the part that remains after performing the division. In the example above, the remainder is `1`. We can write this as:

`9-:2=4text( R)1` 

We read this equation: “Nine divided by two equals four with a remainder of `1`.”

You might be thinking you could split that extra piece of chocolate in parts to share it. This is great thinking! If you split the chocolate in half, you could give each person another half of a piece of chocolate. They would each get `4 1/2` pieces of chocolate. We are not going to worry about expressing remainders as fractions or decimals right now. We are going to use the remainder notation with the letter R. Here’s an example:

Example

Problem

`45-:6`

 

 

 

`6 * 7 = 42`

How many sixes are there in `45`? Try `7`.

 

 

`45 - 42 = 3`

`3` is not enough for another `6`. So, `3` is the remainder.

 

Answer

`45-:6=7text( R)3`

 

 

 
         

Since multiplication is the inverse of division, you can check your answer to a division problem with multiplication. To check the answer `7" R"3`, first multiply `6` by `7` and then add `3`.

`6 * 7 = 42`

`42 + 3 = 45`, so the quotient `7" R"3` is correct.

Compute `67-:7`. 

 

A) `9`

 

B) `9" R"4`

 

C) `60`

 

D) `10`

 

+ 

Show/Hide Answer

 

Performing Long Division

Long division is a method that is helpful when you are performing division that you cannot do easily in your head, such as division involving larger numbers. Below is an example of a way to write out the division steps.

Example

Problem

`68-:4` 

 

 

 

The image shows a long division problem. The dividend is 68 and the divisor is 4.

Rewrite the division.

 

 

 

The image shows a long division problem. The dividend is 68, the divisor is 4, and the quotient is 1. Multiply the quotient, 1, by the divisor, which equals 4 and is placed below the 6 in the dividend. 4 is subtracted from 6, which equals 2. Bring down the 8 from the dividend to make 28.

Divide the tens.

What is `6` divided by `4`?

`4*1=4`, so write a `1` above the `6`. 

Subtract `4` from `6` and bring down the next digit of the dividend, `8`.

 

 

 

What is `28` divided by `4`?

 

 

 

The image shows a long division problem. The dividend is 68 and the divisor is 4. The quotient is 17. Multiply the 1 in the quotient by the divisor, which equals 4 and is placed below the 6 in the dividend. 4 is subtracted from 6, which equals 2. Bring down the 8 from the dividend to make 28. Next, the 7 in the quotient is multiplied by the divisor resulting in 28, which is subtracted from 28 in the line above it. The remainder is 0.

 

`7 * 4 = 28`, so write a `7` above the `8`.

There is no remainder.

 

 

 

`17 * 4`

The image shows a multiplication problem with numbers aligned by place value shows 17 times 4 equals 68. A small 2 is next to the 1 in 17.

 

Check your answer using multiplication.

 

 

 

Answer

`68-:4=17`

 

 

 
         

Example

Problem

`6,707-:233` 

 

 

 

The image shows a long division problem. The dividend is 6707 and the divisor is 233. A 2 is placed over the 0 in the dividend 6707.

 

 

 

 

 

 

Examine the first `3` digits of the dividend and determine how many `233`s are in it.

Use guess and check.

Try: `2 * 233 = 466`

Try: `3 * 233 = 699` (too large)

 

 

 

The image shows a long division problem. The dividend is 6707 and the divisor is 233. A 2 is placed over the 0 in the dividend 6707. Multiply the quotient, 2, by the divisor, which equals 466 and is subtracted from 670, which equals 204. Bring down the 7 from the dividend to make 2047.

 

Subtract `466` from `670` and bring down the next digit of the dividend, `7`.

 

 

The image shows a long division problem. The dividend is 6707 and the divisor is 233. A 2 is placed over the 0 in the dividend 6707. Multiply the quotient, 2, by the divisor, which equals 466 and is subtracted from 670, which equals 204. Bring down the 7 from the dividend to make 2047. Next, determine how many times 233 goes into 2047. 8 times, so the 8 in the quotient is multiplied by the divisor resulting in 1864, which is subtracted from 2047, and equals a remainder of 183.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

How many `233`s are in `2,047`? It looks like close to `10` because `233*10=2,330`. 

Try `9`. `233*9` equals `2,097`.

 

 

`2,097` (Too large)

 

Must be `8`!

 

 

 

 

`233 * 28 = 6,524`

`6,524 + 183 = 6,707`

Check your answer using multiplication.

First, multiply `233*28`. 

Then, add the remainder.

 

Answer      `6,707-:233=28text( R)183` 

 

Compute `417-:34`.  

 

A) `451`

 

B) `12`

 

C) `12" R"9`

 

D) `13`

 

+ 

Show/Hide Answer

 

Dividing Whole Numbers by a Power of `10`

Just as multiplication by powers of `10` results in a pattern, there is a pattern with division by powers of `10`. Consider three quotients: `20-:10`; `200-:10`; `2,000-:10`.

Think about `20-:10`. There are `2` tens in twenty, so `20-:10=2`. The computations for `200-:10` and `2,000-:10` are shown below.

Example

Problem

`200-:10`

 

 

 

The image shows a long division problem. The dividend is 200 and the divisor is 10.

Rewrite the problem.

 

 

The problem highlights whether 10 goes into 2.

Divide the first digit of the dividend, `2`, by the divisor.

Since `2-:10` does not give a whole number, go to the next digit, `0`.

 

 

The problem highlights whether 10 goes into 20. A 2 is placed above the first 0 in the dividend 200.

 

`20-:10 = 2`

 

 

The problem works out 2 times 10. The answer 20 is below the dividend as a subtraction problem. 20 minus 20 equals 0.

`2 * 10 = 20`

`20 - 20 = 0`

 
 

The problem highlights the second 0 in the dividend 200 brought down to the answer of the subtraction problem, showing 0 0.

 

 

Bring down the next digit of the dividend, which is `0`.

 

  
 

The problem highlights 10 goes into 0, 0 times. A 0 is added above to the dividend to show the answer 20.

 

 

 

Since `10` still does not go into `00` and we have nothing left to bring down, multiply the `0` by `10`.

 

  

 

 

`0*10=0`

`0 - 0 = 0`

We have no remainder.

 

Answer

`200-:10 = 20`

 

 

 

Example

Problem

`2000-:10`

 

 

 

The image shows a long division problem. The dividend is 2000 and the divisor is 10.

Rewrite the problem.

 

 

The problem highlights whether 10 goes into 2.

Divide the first digit of the dividend, `2`, by the divisor.

Since `2-:10` does not give a whole number, go to the next digit, `0`.

 

 

The problem highlights whether 10 goes into 20.

`20-:10=2`

 

 

The problem highlights whether 10 goes into 20. A 2 is placed above the first 0 in the dividend 2000.

 

`2 * 10 = 20`

`20 - 20 = 0`

 

 

 

The problem works out 2 times 10. The answer 20 is below the dividend as a subtraction problem. 20 minus 20 equals 0.

 

 

Bring down the next digit, `0`, of the dividend.

 
 

The problem highlights the third 0 in the dividend 2000 brought down to the answer of the subtraction problem, showing 0 0 0.

Since `10` does not go into `00`, add a `0` to the quotient and bring down the next digit, `0`.

  

 

The problem highlights 10 goes into 0, 0 times. A 0 is added above to the dividend to show the answer 200.

 

 

 

Since `10` still does not go into `000` and we have nothing left to bring down, add a `0` to the quotient, multiply the `0` by `10`.

`0*10 = 0`

`0 - 0 = 0`

We have no remainder.

 

Answer

`2,000-:10 = 200`

 

 

Examine the results of these three problems to try to determine a pattern in division by `10`.

`20` `text()-:text()` `10=2`
`200` `text()-:text()` `10=20`
`2,000` `text()-:text()` `10=200`

Notice that the number of zeros in the quotient decreases when a dividend is divided by `10`: `20` becomes `2`; `200` becomes `20` and `2,000` become `200`. In each of the examples above, you can see that there is one fewer `0` in the quotient than there was in the dividend.

Continue another example of division by a power of `10`.

Example

Problem

`2,000-:100`

 

 

 

The image shows a long division problem. The dividend is 2000 and the divisor is 100.

Rewrite the problem.

 

 

The problem highlights whether 100 goes into 2.

Divide the first digit of the dividend, `2`, by the divisor.

Since `2-:100` does not give a whole number, go to the next digit, `0`.

 

 

The problem highlights whether 100 goes into 20.

Divide the first two digits of the dividend, `20`, by the divisor.

Since `20-:100`  does not give a whole number, go to the next digit, `0`.

 

 

The problem highlights whether 100 goes into 200.

`200-:100=2`

 

 

The problem works out 2 times 100. The answer 200 is below the dividend as a subtraction problem. 200 minus 200 equals 0.

`2 * 100 = 200`

`200 - 200 = 0`

 
 

The problem highlights the third 0 in the dividend 2000 brought down to the answer of the subtraction problem, showing 0 0.

 

 

Bring down the next digit, `0`, of the dividend.

 

  

 

The problem highlights 100 goes into 0, 0 times. A 0 is added above to the dividend to show the answer 20.

 

 

 

 

 

 

 

 

Since `100` still does not go into `00` and we have nothing left to bring down, add a `0` to the quotient, multiply the `0` by `10`.

`0*10 = 0`

`0 - 0 = 0`

We have no remainder.

 

Answer

`2,000-:100=20`

 

 

Consider this set of examples of division by powers of `10`. What pattern do you see?

`20` `text()-:text()` `10=2`
`200` `text()-:text()` `10=20`
`2,000` `text()-:text()` `10=200`
`2,000` `text()-:text()` `100=20`
`2,000` `text()-:text()` `1,000=2`

Notice that when you divide a number by a power of `10`, the quotient has fewer zeros. This is because division by a power of `10` has an effect on the place value. For example, when you perform the division `18,000-:100=180`, the quotient, `180`, has two fewer zeros than the dividend, `18,000`. This is because the power of `10` divisor, `100`, has two zeros.

Compute `135,000-:100`.

 

A) `13,500`

 

B) `134,900`

 

C) `13,500,000`

 

D) `1,350`

 

+ 

Show/Hide Answer

 

Division by Zero

You know what it means to divide by `2` or divide by `10`, but what does it mean to divide a quantity by `0`? Is this even possible? Can you divide `0` by a number? Consider the two problems written below.

`0/8` and `8/0`

 

We can read the first expression, “zero divided by eight” and the second expression, “eight divided by zero.” Since multiplication is the inverse of division, we could rewrite these as multiplication problems.

`0-:8=?`

`?*8 = 0`

The quotient must be `0` because `0*8=0`.

`0/8=0`

Now let’s consider `8/0`.

`8-:0=?`

`?*0=8`

This is not possible. There is no number that you could multiply by zero and get eight. Any number multiplied by zero is always zero. There is no quotient for `8/0`. There is no quotient for any number when it is divided by zero.

Division by zero is an operation for which you cannot find an answer, so it is not allowed. We say that division by `0` is undefined.

Using Division in Problem Solving

Division is used in solving many types of problems. Below are three examples from real life that use division in their solutions.

Example

Problem

 

 

 

Luana made `40` empanadas for a party. If the empanadas are divided equally among `12` guests, how many will each guest have? Will there be any leftover empanadas?

 

 
 

`40-:12`

Since each guest will have an equal share, we can use division.

  
 

The image shows a long division problem. The dividend is 40, the divisor is 12, and the quotient is 3. Multiply the quotient, 3, by the divisor, which equals 36 and is placed below the 40 in the dividend. Subtract 36 from the dividend, 40, which equals a remainder of 4.

 

 

 

Use trial and error. Try `3`.

`12 * 3 = 36`

  

 

 

When `40` empanadas are divided equally among `12` people, there are `4` left over.

 

Answer

Each guest will have `3` empanadas. There will be `4` empanadas left over.

 
             

Example

Problem

 

A case of floor tiles has `12` boxes in it. The case costs `$384`. How much does one box cost?

 

 

 

`384-:12`

Since the boxes each cost the same amount, you want to divide `$384` into `12` equal parts.

 

 

The image shows a long division problem. The dividend is 384, the divisor is 12.

Perform the division.

Try to divide the first digit in the dividend by the divisor. `12` will not divide into `3`, so go to the next digit.

 

 

The problem shows that the number 3 is above the 8 in the dividend 384. The answer to 3 times 12, 36 is placed under the 38 in the dividend to create a subtraction problem, 38 minus 36.

Perform `38-:12`.

Pick a quotient and test it. Try `3`.

`3 * 12 = 36`.

 

 

The problem shows that the answer to the subtraction 38 minus 36 equals 2.

Subtract `36` from `38`.

 

 

 

The problem shows that the 4 from the dividend is brought down and added to the 2 from the subtraction creating the number 24. 12 goes into 24, 2 times. 2 is added to the line above the dividend. 2 times 12 equals 24. 24 minus 24 equals 0 so there is no remainder. The problem, 384 divided by 12 shows the quotient is 32.

 

Bring the next digit of the dividend down and perform division.

`12 * 2 = 24`

`24 - 24 = 0`

 

 

The image shows the multiplication problem 32 times 12, and is broken into 32 times 2 equals 64, 32 times 10 equals 320; 64 plus 320 equals 384.

 

 

 

 

Does `32 * 12` equal `384`?

Check your answer by multiplying.

Yes! The answer is correct!

 

 

Answer

Each box of tiles costs `$32`.

 

 
           

Example

Problem

 

 

A banana grower is shipping `4,644` bananas. There are `86` crates, each containing the same number of bananas. How many bananas are in each crate?

 

 

 

`4,644-:86`

Since each crate, or box, has the same number of bananas, you can take the total number of bananas and divide by the number of crates.

Rewrite the division.

 

 

The image shows a long division problem. The dividend is 4644, the divisor is 86.

 

 

 

Use trial and error to determine what `464-:86` equals.

Try `5`:

A multiplication problem shows that 86 times 5 equals 430.

 

 

 

The problem shows that the number 5 is above the 6 in the dividend 4644. The answer to 5 times 86, 430 is placed under the 464 in the dividend to create a subtraction problem, 464 minus 430. The answer to the subtraction is 34. The second 4 from the dividend is brought down and added to the 34 from the subtraction, creating the number 344.

`464 - 430 = 34`

Then, bring down the next digit of the dividend, `4`.

 

 

The problem shows that 86 goes into 344 four times. 4 is added to the line above the dividend. 4 times 86 equals 344. 344 minus 344 equals 0 so there is no remainder. The problem 4644 divided by 86 shows the quotient is 54.

 

Use trial and error to determine the quotient of `344` and `86`.

Try `4`:

A multiplication problem shows that 86 times 4 equals 344.

 

 

 

 

The image shows the multiplication problem 86 times 54, and is broken into 86 times 4 equals 344, 86 times 50 equals 4300; 344 plus 4300 equals 4644.

Check your answer by multiplying.

 

Yes! The answer is correct!

 

Answer

Each crate contains `54` bananas.

 

 
           

A theater has `1,440` seats. The theater has `30` rows of seats. How many seats are in each row?

 

A) `1,410`

 

B) `48`

 

C) `43,200`

 

D) `480`

 

+ 

Show/Hide Answer

 

Summary

Division is the inverse operation of multiplication, and can be used to determine how to evenly share a quantity among a group. Division can be written in three different ways: using a fraction bar, using a division symbol, and using long division. Division can be represented as splitting a total quantity into sets of equal quantities, as skip subtracting on the number line, and as a dimension with an area model. Remainders may result when performing division and they can be represented with the letter R, followed by the number remaining. Since division is the inverse operation of multiplication, you need to know your multiplication facts in order to do division. For larger numbers, you can use long division to find the quotient.