
Multiplying Whole Numbers and Applications
Multiplication is one of the four basic arithmetic operations (along with addition, subtraction, and division.) People use multiplication for a variety of everyday tasks including calculating the cost to purchase multiple items that are the same price, determining sales tax, and finding area and other geometric measures. If you wanted to calculate the cost of `6` baseball caps at `$14.00` each, you could add `14.00 + 14.00 + 14.00 + 14.00 + 14.00 + 14.00`, or use multiplication, which is a shortcut for repeated addition.
Instead of adding the same number over and over again, an easier way to reach an answer is to use multiplication. Suppose you want to find the value in pennies of `9` nickels. You can use addition to figure this out. Since a nickel is worth `5` pennies, or `5` cents, you can find the value of `9` nickels by adding `5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5`. This repeated addition shows that `9` nickels have a value of `45` cents.
All of this addition can become very tiring. So, the math operation called multiplication can help perform repeated addition of whole numbers much more quickly. To find the value of these nickels, you could write a multiplication equation: `5 * 9 = 45`.
`5 * 9 = 45` is read “`5` times `9` equals `45`” or “`5` multiplied by `9` is equal to `45`.” The numbers that are being multiplied are called factors A number that is multiplied by another number or numbers to get a product. For example, in the equation `4 * 5 = 20`, `4` and `5` are factors. . The factors in this example are `5` and `9`. The result of the multiplication (or the answer) is called the product The result when two numbers are multiplied. For example, the product of `4 * 5` is `20`. . The product for `5 * 9` is `45`.
In addition to showing multiplication as `5 * 9 = 45`, you can show multiplication by using the x sign, `5 text( x )9 = 45`, and also with parentheses, `(5)(9) = 45` or `5(9) = 45`.
|
Three Ways to Write Multiplication
Using a multiplication or times sign: `2text( x )3=6` Using a dot: `2 * 3 = 6` (this dot is NOT a decimal point) Using parentheses: `(2)(3) = 6` or `2(3) = 6`
|
When you are adding the same number over and over again, you can use multiplication. You take the number that you are adding and rewrite it as a multiplication problem, multiplying it by the number of times you are adding it. For example, if you were serving `2` cookies each to `13` children, you could add `2` thirteen times or you could use multiplication to find the answer.
`2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 2*13 = 26`
You could also write this using parentheses: `2(13) = 26`
In order to understand what multiplication is, consider three different ways to think about multiplication of whole numbers.
Approach `1`: Set Model
Multiplication is a way of writing repeated addition. When you read the problem `3 * 5` you could think of this as `3` groups of `5` things: `3` plates with `5` cookies on each plate; `3` baskets, each with `5` oranges in it; or `3` piles with `5` coins in each pile. We could show this as a picture:

`3 * 5 = 3` groups of `5 = 15`
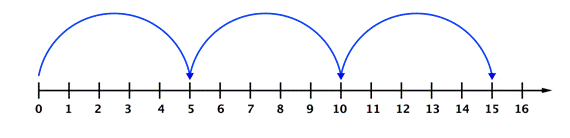
Approach `2`: Number Line Model
Multiplication can also be shown on a number line. The problem, `3 * 5` is modeled on the number line below. You can see that the arrows cover a distance of `5` units at a time. After `3` “jumps” on the number line, the arrow ends at `15`.
Approach `3`: Area Model
Another way of thinking about multiplication is to think about an array or area model to represent multiplication. You could think of `3 * 5` as `3` rows of `5` things. This might be a box of chocolates that has `3` rows of `5` chocolates, or a meeting room that is set up with `3` rows of `5` chairs. The pictures below show two rectangular arrangements of `3 * 5`.
|
|
|
Do you see how both pictures represent the product `15`? The picture on the left shows an area of `3` by `5`. If you count the small squares that make up the rectangle, they total `15`. Similarly, in the picture on the right, you see that `3` rows of `5` circles is equal to `15` circles.
|
Example |
||||
|
Problem
|
What is the product of `4*6` ? Use the set model, number line model and area model to represent the multiplication problem. |
|
|
|
|
|
Set Model:
Number Line model:
|
|
|
|
|
|
Area Model:
|
|
|
|
|
Answer `4 * 6 = 24` |
|
|
|
|
If you switch the order in which you multiply two numbers, the product will not change. This is true for any two numbers you multiply. Think about the problem shown above.
You could make `6` jumps of `4` or `4` jumps of `6` on the number line and end up at `24`.
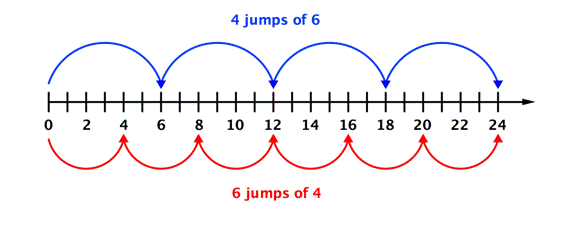
Or, you could make `6` rows of `4` or `4` rows of `6` and still have `24` squares.
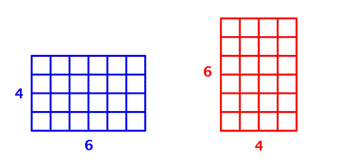
`6 * 4 = 24` and `4 * 6 = 24`.
|
Tanisha modeled `5 * 8` using the following models. Which models are accurate representations of the multiplication of these two factors?
`#1`
`#2`
`#3`
A) All three models accurately represent `5 * 8`.
B) Only models `#1` and `#3` accurately represent `5 * 8`.
C) Only models `#2` and `#3` accurately represent `5 * 8`.
D) None of the models accurately represents `5*8`.
|
Let’s go back to the question posed at the opening of this topic of study. How can you use multiplication to figure out the total cost of `6` baseball caps that cost `$14` each? (You do not have to pay sales tax). You can figure out the cost by multiplying `14 * 6`.
One way to do this computation is to break `14` down into parts and multiply each part by `6`.
| `14` | `text()=text()` | `10+4` |
So, |
| `14*6` | `text()=text()` | `10*6+4*6` | |
| `text()=text()` | `60+24` | ||
| `text()=text()` | `84` |
You may recall the multiplication computed as `14*6`:
In this notation, some of the steps are written down with special notation. The product of `6` and `4` (`24`) is written by putting the `4` in the ones place and writing a `2` up above the `1`. This `2` actually stands for `20`. Then, `6` is multiplied by `1`. We are actually multiplying `6` by `1` ten and adding `20` to get the `80` in `84`.
An example of multiplying two two-digit numbers is shown below. When performing this multiplication, each part of each number is multiplied by the other number. The numeric notation and an accompanying description are provided.
|
Example |
||||
|
Problem |
`47*52` |
|
|
|
|
|
|
Stack the numbers with the place values aligned.
|
|
|
|
|
|
Multiply the ones. `2 " x " 7 = 14` ones. Write `4` ones in the ones place and regroup `10` ones into the tens place. |
|
|
|
|
|
Multiply `2` ones by `4` tens, and add the regrouped `1` ten. `2` ones times `4` tens `text(+ )1` ten `text(= )9` tens
|
|
|
|
|
|
Multiply the tens. `5text( x )7 = 35` tens. Write `5` tens in the tens place and regroup.
|
|
|
|
|
|
Multiply: `5` tens times `4` tens `text(= )20` hundreds. Add the regrouped `3`, which is `3` hundred. |
|
|
|
|
|
Add the two lines. `94+2,350`
|
|
|
|
Answer `47 * 52 = 2,444` |
||||
Notice that you are multiplying each of the parts of each number by the parts of the other number. You are doing so in a systematic way, from ones places to tens places. You are also using notation to keep track of what you have regrouped. These are shown with raised numbers.
To keep your columns straight and your work organized, consider using grid paper or lined paper turned sideways so the lines form columns. Here is an example of a problem written on grid paper:
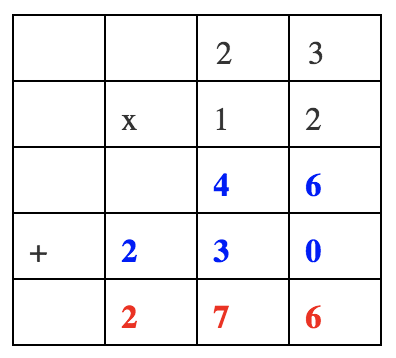
When you are multiplying whole numbers, be sure to line up the digits by their place values. In the example above, the digits in the ones place are lined up: the `2` in `12` is directly below the `3` in `23`.
When you multiply numbers by `10` or powers of `10` (`100`; `1,000`; `10,000`; `100,000`), you’ll discover some interesting patterns. These patterns occur because our number system is based on ten: ten ones equal ten; ten tens equal one hundred; ten hundreds equal one thousand. Learning about these patterns can help you compute easily and quickly.
Consider the example of `25 * 100`. First, let’s use the standard algorithm method to multiply these numbers.
|
Example |
||||
|
Problem |
`25*100` |
|
|
|
|
|
|
|
|
|
|
Answer |
`25 * 100 = 2,500` |
|
|
|
Using the standard algorithm, we calculated `25 * 100 = 2,500`.
Look at the table below to find a pattern in the factors and products. See how the number of zeros in the power of `10` (`10`, `100`, `1,000`, etc.) relates to the number of zeros in the product.
|
Factors |
Product |
|
`5 * 10` |
`=50` |
|
`5 * 100` |
`=500` |
|
`5 * 1,000` |
`=5,000` |
|
`5 * 10,000` |
`=50,000` |
You can see that the number of zeros in the product matches the number of zeros in the power of `10` (`10`, `100`, `1,000`, etc.). Will this always be true or is it true only in certain situations? Look at two more patterns:
|
Factors |
Product |
|
`10 * 10` |
`=100` |
|
`10 * 100` |
`=1,000` |
|
`10 * 1,000` |
`=10,000` |
|
`10 * 10,000` |
`=100,000` |
|
Factors |
Product |
|
`120 * 10` |
`=1,200` |
|
`120 * 100` |
`=12,000` |
|
`120 * 1,000` |
`=120,000` |
|
`120 * 10,000` |
`=1,200,000` |
Notice that in these last two examples, both factors had zeros in them. The number of zeros in the product is equal to the sum of the number of zeros at the end of each of the factors.
The example below illustrates how to multiply `140 * 3000`.
|
Example |
||||
|
Problem |
`140*3000` |
|
|
|
|
|
|
Identify the non-zero parts of the factors and multiply these parts.
Multiply `3` ones by `4` ones. `4 * 3 = 12`. Write `2` in the ones place and regroup the `1` ten. |
|
|
|
|
Count the number of zeros in each factor.
`140` has one zero; `3,000` has three zeros. `1 + 3 = 4` Write another `4` zeros after the `42`. |
|
||
|
Answer |
`140 * 3000 = 420,000` |
|
|
|
|
Multiplying by Ten When you multiply a whole number by `10` or a power of `10`, first multiply the nonzero parts of the numbers. Then include the number of zeros at the end of the product equal to the total number of zeros at the end of the factors. `13 * 100 = 1,300` `180 * 2,000 = 360,000` |
|
An apple orchard sold `100` bags of apples. If there are `30` apples in each bag, how many apples did the orchard sell?
A) `130`
B) `300`
C) `30,000`
D) `3,000`
|
Sometimes you don’t need an exact product because an estimate is enough. If you’re shopping, stopping to make a calculation with pencil and paper, or even a calculator, is inconvenient. Usually, shoppers will round numbers up so they will be sure that they have enough money for their purchases.
Estimating products is also helpful for checking an answer to a multiplication problem. If your actual calculation is quite different from your estimate, there is a good chance you have made a place value and/or regrouping mistake.
To estimate a product, you often round the numbers first. When you round numbers, you are always rounding to a particular place value, such as the nearest thousand or the nearest ten. If you are rounding a number to the nearest ten, you round it to the ten that is closest to the original number. An example of this is rounding `317` to the nearest ten. In this case, you round `317` to `320`. If the number is half way in between (`315`), generally round up to `320`.
Rounding factors can make it easy to multiply in your head. Let’s consider the multiplication problem `145 * 29`. To estimate this product by rounding, you can round to the nearest ten.
|
Example |
||||
|
Problem |
Use rounding to estimate the product of `145*29`. |
|
|
|
|
|
`150 * 30`
|
Round numbers to the nearest ten. |
|
|
|
|
`15 * 3 = 45` |
Multiply the non-zero numbers. |
|
|
|
|
`4,500`
|
Count the zeros in the factors and include that many zeros after the `45`. |
|
|
|
Answer The estimate of `145 * 29` is `4,500`. |
||||
You can use a calculator to see if your estimate seems reasonable. Or you can use estimation to make sure that the answer that you got on a calculator is reasonable. (Have you ever input the wrong numbers?)
|
|
Key entries: `145` `text(x)` `29` `=` Result: `4,205` The exact product and the estimate are close enough to give you confidence in your calculations. |
|
A factory produces `58` packages of cookies in one hour. There are `32` cookies in each package. Which is the best estimate of the number of cookies the factory produces in one hour?
A) `1,800`
B) `1,500`
C) `18,000`
D) `180`
|
The formula for the area of a rectangle uses multiplication: length `*` width `=` area. Applying what you know about multiplication, you can find the area of any rectangle if you know its dimensions (length and width). Consider the rectangle that is `4` by `7` shown below. Its length is `7` and its width is `4`.
You can divide the rectangle into units by making `7` columns and `4` rows.
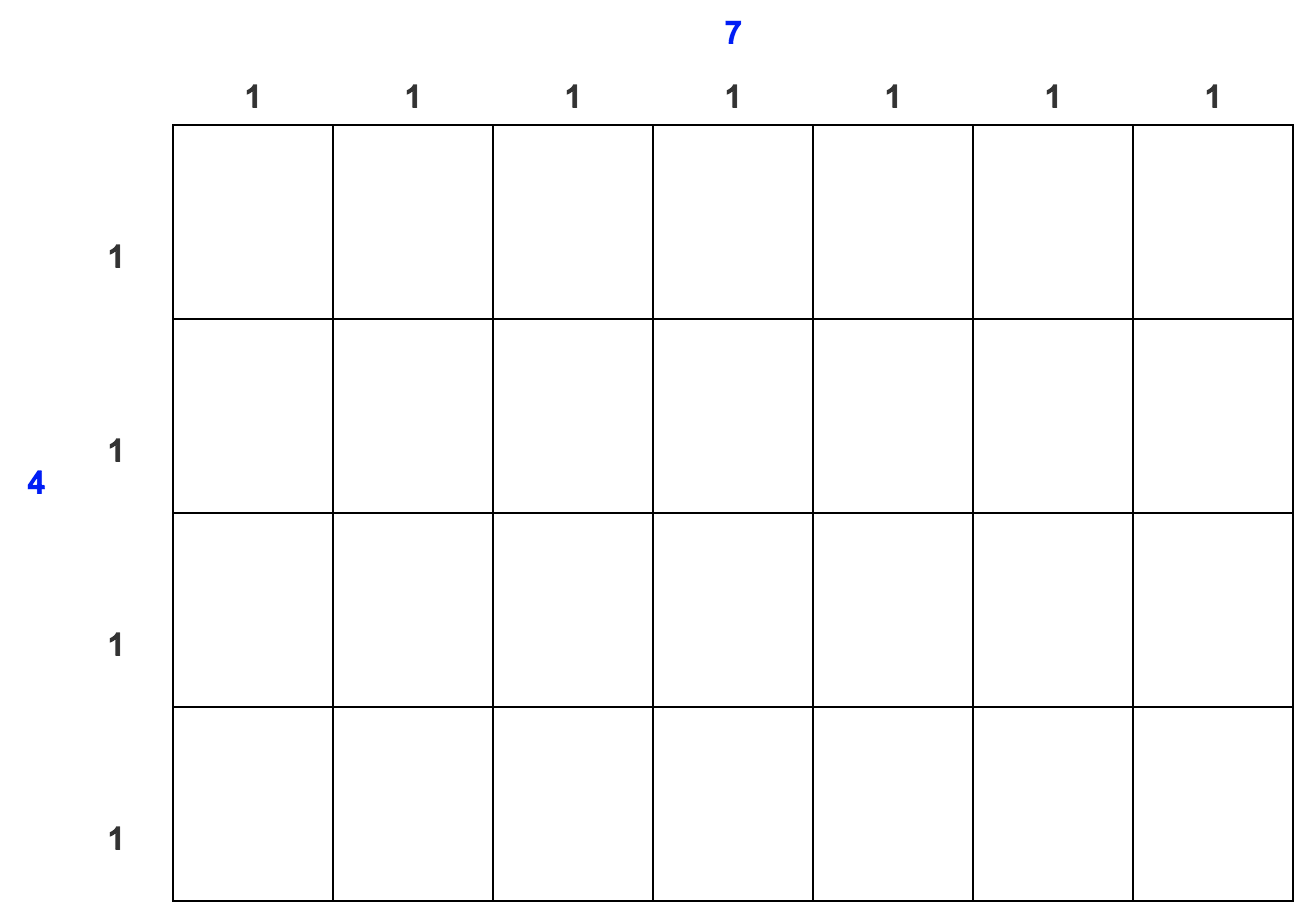
You can see that dividing the rectangle in this way results in `28` squares. You could say that the area of the rectangle is `28` square units. You could also find the area by multiplying `7 * 4`. (Note: Area is always measured in square units: square inches, square centimeters, square feet, etc.)
Consider an example of a larger rectangle, like one that is found on a soccer field. At each end of a soccer field, centered at the goal, is a large rectangle. This rectangle is called the penalty box because fouls committed within the lines of this rectangle may result in a penalty kick. On a regulation soccer field, the penalty box is `44` yards by `18` yards. What is the area of a penalty box?
|
Example |
||||
|
Problem |
`44text( yards)* 18text( yards)` |
|
|
|
|
Answer |
The area of the penalty box is `792` square yards. |
|
|
|
|
What is the area of a rectangle whose length is `23` feet and whose width is `7` feet?
A) `30` feet
B) `161` feet
C) `161` square feet
D) `1,421` square feet
|
Multiplication is used in solving many types of problems. Below are two examples that use multiplication in their solutions to the problem.
|
Example |
|||||
|
Problem
|
A case of cat food has two layers. Each layer has `4` rows of `6` cans. How many cans are in a case of cat food? |
|
|
||
|
|
|
First find the number of cans in one layer. You can multiply to figure this out.
|
|
||
|
|
Since there are two layers, you multiply the number of cans in one layer by `2`.
|
|
|||
|
Answer |
There are `48` cans in a case of cat food. |
|
|||
|
Example |
||||||
|
Problem |
A theater has `45` rows with `40` seats in each row. How many seats are there in the theater? |
|
|
|||
|
|
|
You can solve this problem by adding `40`, `45` times, but that would take a lot of work. Multiplication is the way to go.
|
|
|||
|
|
|
|
|
|||
|
Answer |
There are `1,800` seats in the theater. |
|
|
|||
|
A lawn care company charges `$35` to mow a lawn. If the company mows `32` lawns, how much money will it make?
A) `$9,760`
B) `$1,120`
C) `$130.00`
D) `$67.00`
|
Multiplication can make repeated addition easier to compute in calculations and problem solving. Multiplication can be written using three symbols: parentheses, a times sign, or a multiplication dot. To perform multiplication with two-digit factors or greater, you can use the standard algorithm where you multiply each of the numbers in each factor by the numbers in the other factor. Using strategies such as short cuts for multiplying by powers of `10` and estimation to check your answers can make multiplication easier as well as reduce errors.