Subtracting Whole Numbers and Applications
Learning Objectives
- Subtract whole numbers without regrouping.
- Subtract whole numbers with regrouping.
- Solve application problems using subtraction.
Introduction
Subtracting involves finding the difference between two or more numbers. It is a method that can be used for a variety of applications, such as balancing a checkbook, planning a schedule, cooking, or travel. Suppose a government official is out of the U.S. on business for `142` days a year, including travel time. The number of days per year she is in the U.S. is the difference of `365` days and `142` days. Subtraction is one way of calculating the number of days she would be in the U.S. during the year.
When subtracting numbers, it is important to line up your numbers, just as with addition. The minuendThe number from which another number is subtracted. is the greater number from which the lesser number is subtracted. The subtrahendThe number that is subtracted from another number. is the number that is subtracted from the minuend. A good way to keep minuend and subtrahend straight is that since subtrahend has “subtra” in its beginning, it goes next to the subtraction sign and is the number being subtracted. The differenceThe quantity that results from subtracting one number from another, or from subtracting the subtrahend from the minuend. is the quantity that results from subtracting the subtrahend from the minuend. In `86 - 52 = 34`, `86` is the minuend, `52` is the subtrahend, and `34` is the difference.
Subtracting Whole Numbers
When writing a subtraction problem, the minuend is placed above the subtrahend. This can be seen in the example below, where the minuend is `10` and the subtrahend is `7`.
|
Example
|
|
Problem
|
`10 - 7=?`
|
|
|
|
Answer `10 - 7 = 3`
|
When both numbers have more than one digit, be sure to work with one place value at a time, as in the example below.
|
Example
|
|
Problem
|
`689 - 353=?`
|
|
|
| |
`6` |
`8` |
`9` |
| `-` |
`3` |
`5` |
`3` |
| |
|
|
`6` |
| |
`6` |
`8` |
`9` |
| `-` |
`3` |
`5` |
`3` |
| |
|
`3` |
`6` |
| |
`6` |
`8` |
`9` |
| `-` |
`3` |
`5` |
`3` |
| |
`3` |
`3` |
`6` |
|
First, set up the problem and align the numbers by place value.
Then, subtract the digits in the ones place, `9-3`.
Next, subtract the digits in the tens place, `8-5`.
Finally, subtract the digits in the hundreds place, `6-3`.
|
|
Answer `689 - 353 = 336`
|
|
| |
|
|
|
Lining up numbers by place value becomes especially important when you are working with larger numbers that have more digits, as in the example below.
|
Example
|
|
Problem
|
`9,864 - 743=?`
|
|
| |
`9` |
`8` |
`6` |
`4` |
| `-` |
|
`7` |
`4` |
`3` |
| |
|
|
|
|
| |
`9` |
`8` |
`6` |
`4` |
| `-` |
|
`7` |
`4` |
`3` |
| |
|
|
|
`1` |
| |
`9` |
`8` |
`6` |
`4` |
| `-` |
|
`7` |
`4` |
`3` |
| |
|
|
`2` |
`1` |
| |
`9` |
`8` |
`6` |
`4` |
| `-` |
|
`7` |
`4` |
`3` |
| |
|
`1` |
`2` |
`1` |
| |
`9` |
`8` |
`6` |
`4` |
| `-` |
|
`7` |
`4` |
`3` |
| |
`9` |
`1` |
`2` |
`1` |
|
First, set up the problem and align the numbers by place value.
Then, subtract the digits in the ones place, `4-3`.
Next, subtract the digits in the tens place, `6-4`.
Now, subtract the digits in the hundreds place, `8-7`.
There is no digit to subtract in the thousands place, so keep the `9`.
|
|
Answer `9,864 - 743= 9,121`
|
| |
|
|
|
Subtract: `2,489 - 345`.
A) `2,144`
B) `1,355`
C) `2,834`
D) `1,134`
A) `2,144`
Correct. You successfully subtracted `345` from `2,489`.
B) `1,355`
Incorrect. You probably did not line up your numbers correctly by place value. The correct answer is `2,144`.
C) `2,834`
Incorrect. You probably added when you should have subtracted. The correct answer is `2,144`.
D) `1,134`
Incorrect. You probably did not subtract correctly in the tens and thousands places. The correct answer is `2,144`.
|
Subtracting Whole Numbers with Regrouping
You may need to regroup when you subtract. When you regroupRewriting a number so you can subtract a greater digit from a lesser digit. , you rewrite the number so you can subtract a greater digit from a lesser one.
When you’re subtracting, just regroup to the next greater place-value position in the minuend and add `10` to the digit you’re working with. As you regroup, cross out the regrouped digit in the minuend and place the new digit above it. This method is demonstrated in the example below.
|
Example
|
|
Problem
|
`3,225 - 476=?`
|
| |
|
|
|
|
| |
`3` |
`2` |
`2` |
`5` |
| `-` |
|
`4` |
`7` |
`6` |
| |
|
|
|
|
| |
|
|
`1` |
`15` |
| |
`3` |
`2` |
`cancel2` |
`cancel5` |
| `-` |
|
`4` |
`7` |
`6` |
| |
|
|
|
`9` |
| |
|
`1` |
`11` |
`15` |
| |
`3` |
`cancel2` |
`cancel2` |
`cancel5` |
| `-` |
|
`4` |
`7` |
`6` |
| |
|
|
`4` |
`9` |
| |
`2` |
`11` |
`11` |
`15` |
| |
`cancel3` |
`cancel2` |
`cancel2` |
`cancel5` |
| `-` |
|
`4` |
`7` |
`6` |
| |
|
`7` |
`4` |
`9` |
| |
`2` |
`11` |
`11` |
`15` |
| |
`cancel3` |
`cancel2` |
`cancel2` |
`cancel5` |
| `-` |
|
`4` |
`7` |
`6` |
| |
`2` |
`7` |
`4` |
`9` |
|
First, set up the problem and align the digits by place value.
Since you can’t subtract `6` from `5`, regroup, so `2` tens and `5` ones become `1` ten and `15` ones. Now you can subtract `6` from `15` to get `9`.
Next, you need to subtract `7` tens from `1` ten. Regroup `2` hundreds as `1` hundred, `10` tens and add the `10` tens to `1` ten to get `11` tens. Now you can subtract `7` from `11` to get `4`.
To subtract the digits in the hundreds place, regroup `3` thousands as `2` thousands, `10` hundreds and add the `10` hundreds to the `1` hundred that is already in the hundreds place. Now, subtract `4` from `11` to get `7`.
Since there is no digit in the thousands place of the subtrahend, bring down the `2` in the thousands place into the answer.
|
|
Answer `3,225 - 476=2,749`
|
| |
|
|
|
Subtract: `1,610 - 880`
A) `1,522`
B) `2,490`
C) `730`
D) `620`
A) `1,522`
Incorrect. You probably did not line up the numbers by place value when you were subtracting. The correct answer is `730`.
B) `2,490`
Incorrect. You probably added the numbers instead of subtracting. The correct answer is `730`.
C) `730`
Correct. You successfully subtracted `880` from `1,610`.
D) `620`
Incorrect. You probably did not regroup correctly. The correct answer is `730`.
|
Checking Your Work
You can check subtraction by adding the difference and the subtrahend. The sum should be the same as the minuend.
|
Example
|
|
Problem
|
Check to make sure that `7` subtracted from `12` is equal to `5`.
|
|
`12 - 7 = 5`
|
Write out the original equation. The minuend is `12`, the subtrahend is `7`, and the difference is `5`.
Next, add the difference, `5`, to the subtrahend, `7`, which results in the number `12`. This confirms that your answer is correct.
|
|
Answer The answer of `5` is correct.
|
| |
|
|
Checking your work is very important and should always be performed when time permits.
Subtracting Numbers Using the Expanded Form
An alternative method to subtract involves writing numbers in expanded form, as shown in the examples below. If you have `4` tens and want to subtract `1` ten, you can just think (`4 - 1`) tens and get `3` tens. Let’s see how that works.
|
Example
|
|
Problem
|
`45 - 12=?`
|
|
| `45` |
`=` |
`40` |
`+` |
`5` |
| `12` |
`=` |
`10` |
`+` |
`2` |
| |
|
|
|
|
|
Let’s write the numbers in expanded form so you can understand what they really mean.
|
|
| `45` |
`=` |
`40` |
`+` |
`5` |
| `12` |
`=` |
`10` |
`+` |
`2` |
| |
|
`30` |
|
|
|
For the tens, the minuend is `40`, or `4` tens. The subtrahend is `10`, or `1` ten. Since `4-1=3`, `4` tens `- text()1` ten `= 3` tens, or `30`.
|
|
| `45` |
`=` |
`40` |
`+` |
`5` |
| `12` |
`=` |
`10` |
`+` |
`2` |
| |
|
`30` |
`+` |
`3` |
|
Now, the ones. `5-2=3`. So, `30+3=33`.
|
|
Answer
|
`45 - 12 = 33`
|
| |
|
|
Now let’s use this method in the example below, which asks for the difference of `467` and `284`. In the tens place of this problem, you need to subtract `8` from `6`. What can you do?
|
Example
|
|
|
Problem
|
`467 - 284=?`
|
|
| `text(Step ) 1text(: Separate by place value)` |
| |
`4text( hundreds)` |
`+` |
`6text( tens)` |
`+` |
`7text( ones)` |
| `-` |
`2text( hundreds)` |
`+` |
`8text( tens)` |
`+` |
`4text( ones)` |
| |
|
|
|
|
|
| `text(Step ) 2text(: Identify impossible differences)` |
| `6-8=[text( )]` |
| `text(Step ) 3text(: Regroup)` |
| |
`3text( hundreds)` |
`+` |
`16text( tens)` |
`+` |
`7text( ones)` |
| `-` |
`2text( hundreds)` |
`+` |
`8text( tens)` |
`+` |
`4text( ones)` |
| |
`1text( hundred)` |
`+` |
`8text( tens)` |
`+` |
`3text( ones)` |
| `text(Step ) 4text(: Combine the parts)` |
| `1text( hundred)+8text( tens)+3text( ones)=183` |
|
Write both the minuend and the subtrahend in expanded form.
Identify differences that are not whole numbers. Since `8` is greater than `6`, you won’t get a whole number difference.
Regroup one of the hundreds from the `4` hundreds into `10` tens and add it to the `6` tens. Now you have `16` tens. Subtracting `8` tens from `16` tens yields a difference of `8` tens.
Combining the resulting differences for each place value yields a final answer of `183`.
|
|
|
Answer `467 - 284 = 183`
|
|
|
|
| |
|
|
|
|
|
|
A woman who owns a music store starts her week with `965` CDs. She sells `452` by the end of the week. How many CDs does she have remaining?
A) `313`
B) `513`
C) `510`
D) `1,417`
A) `313`
Incorrect. You probably made an error when you were subtracting digits in the hundreds place. The correct answer is `513`.
B) `513`
Correct. You successfully subtracted `452` from `965`. In expanded form, `513` is `5` hundreds, `1` ten, and `3` ones.
C) `510`
Incorrect. You probably made an error when you were subtracting digits in the ones place. The correct answer is `513`.
D) `1,417`
Incorrect. You probably added instead of subtracted. The correct answer is `513`.
|
|
Example
|
|
Problem
|
`45 - 17=?`
|
|
| `45` |
`=` |
`40` |
`+` |
`5` |
| `17` |
`=` |
`10` |
`+` |
`7` |
| |
|
|
|
|
|
When you try to subtract `17` from `45`, you would first try to subtract `7` from `5`. But `5` is less than `7`.
Let’s write the numbers in expanded form so you can see what they really mean.
|
|
| `45` |
`=` |
`30` |
`+` |
`15` |
| `17` |
`=` |
`10` |
`+` |
`7` |
| |
|
|
|
|
|
Now, regroup `4` tens as `3` tens and `10` ones. Add the `10` ones to `5` ones to get `15` ones, which is greater than `7` ones, so you can subtract.
|
|
| |
`45` |
`=` |
`30` |
`+` |
`15` |
| `-` |
`17` |
`=` |
`10` |
`+` |
`7` |
| |
|
|
`20` |
`+` |
`8` |
|
Finally, subtract `7` from `15`, and `10` from `30` and add the results: `20 + 8 = 28`.
|
|
Answer
|
`45 - 17 = 28`
|
| |
|
|
Solve Application Problems Using Subtraction
You are likely to run into subtraction problems in everyday life, and it helps to identify key phrases in a problem that indicate that subtraction is either used or required. The following phrases appear in problem situations that require subtraction.
|
Phrase or word
|
Example problem
|
|
Less than
|
The cost of gas is `42` cents per gallon less than it was last month. The cost last month was `280` cents per gallon. How much is the cost of gas this month?
|
|
Take away
|
Howard made `84` cupcakes for a neighborhood picnic. People took away `67` cupcakes. How many did Howard have left?
|
|
Decreased by
|
The temperature was `84^@` Fahrenheit in the early evening. It decreased by `15^@` overnight. What was the temperature in the morning?
|
|
Subtracted from
|
Jeannie works in a specialty store on commission. When she sells something for `$75`, she subtracts `$15` from the `$75` and gives the rest to the store. How much of the sale goes to the store?
|
|
The difference
|
What is the difference between this year’s rent of `$1,530` and last year’s rent of `$1,450`?
|
|
Fewer than
|
The number of pies sold at this year’s bake sale was `15` fewer than the number sold at the same event last year. Last year, `32` pies were sold. How many pies were sold this year?
|
When translating a phrase such as “`5` fewer than `39`” into a mathematical expression, the order in which the numbers appears is critical. Writing `5 - 39` would not be the correct translation. The correct way to write the expression is `39 - 5`. This results in the number `34`, which is `5` fewer than `39`. The chart below shows how phrases with the key words above can be written as mathematical expressions.
|
Phrase
|
Expression
|
|
three subtracted from six
|
`6 - 3`
|
|
the difference of ten and eight
|
`10 - 8`
|
|
Nine fewer than `40`
|
`40 - 9`
|
|
Thirty-nine decreased by fourteen
|
`39 - 14`
|
|
Eighty-five take away twelve
|
`85 - 12`
|
|
Four less than one hundred eight
|
`108 - 4`
|
|
Example
|
|
Problem
|
Each year, John is out of the U.S. on business for `142` days, including travel time. The number of days per year he is in the U.S. is the difference of `365` days and `142` days. How many days during the year is John in the U.S.?
|
|
| |
`3` |
`6` |
`5` |
| `-` |
`1` |
`4` |
`2` |
| |
|
|
|
| |
`3` |
`6` |
`5` |
| `-` |
`1` |
`4` |
`2` |
| |
|
|
`3` |
| |
`3` |
`6` |
`5` |
| `-` |
`1` |
`4` |
`2` |
| |
|
`2` |
`3` |
| |
`3` |
`6` |
`5` |
| `-` |
`1` |
`4` |
`2` |
| |
`2` |
`2` |
`3` |
|
The words “the difference of” suggest that you need to subtract to answer the problem.
First, write out the problem based on the information given and align numbers by place value, `365-142`.
Then, subtract numbers in the ones place, `5-2`.
Subtract numbers in the tens place, `6-4`.
Finally, subtract numbers in the hundreds place, `3-1`.
|
|
Answer John is in the U.S. for `223` days during the year.
|
| |
|
|
|
To make sure he was paid up for the month on his car insurance, Dave had to pay the difference of the amount on his monthly bill, which was `$289`, and what he had paid earlier this month, which was `$132`. Write the difference of `$289` and `$132` as a mathematical expression.
A) `132 - 289`
B) `289 + 132`
C) `132 + 289`
D) `289 - 132`
A) `132 - 289`
Incorrect. Dave had paid `$132`, so that `$132` can be taken away from the full `$289` he owed for the month. The correct answer is `289 - 132`.
B) `289 + 132`
Incorrect. Dave owes the difference of `132` and `289`, not the sum of `289` and `132`. The correct answer is `289 - 132`.
C) `132 + 289`
Incorrect. Dave owes the difference of `132` and `289`, not the sum of `132` and `289`. The correct answer is `289 - 132`.
D) `289 - 132`
Correct. The difference of `289` and `132` can be written as `289 - 132`.
|
|
Example
|
|
Problem
|
An African village is now getting cleaner water than it used to get. The number of cholera cases in the village has declined over the past five years. Using the graph below, determine the difference between the number of cholera cases in `2005` and the number of cases in `2010`.
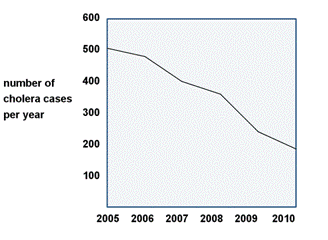
|
|
|
The words “the difference” suggest that you need to subtract to answer the problem.
First, use the graph to find the number of cholera cases per year for the two years: `500` in `2005` and `200` in `2010`.
Then write the subtraction problem and align numbers by place value. Subtract the numbers as you usually would.
|
|
Answer `500 - 200 = 300` cases
|
| |
|
|
Summary
Subtraction is used in countless areas of life, such as finances, sports, statistics, and travel. You can identify situations that require subtraction by looking for key phrases, such as difference and fewer than. Some subtraction problems require regrouping to the next greater place value, so that the digit in the minuend becomes greater than the corresponding digit in the subtrahend. Subtraction problems can be solved without regrouping, if each digit in the minuend is greater than the corresponding digit in the subtrahend.
In addition to subtracting using the standard algorithm, subtraction can also can be accomplished by writing the numbers in expanded form so that both the minuend and the subtrahend are written as the sums of their place values.
