Adding Whole Numbers and Applications
Learning Objectives
- Add whole numbers without regrouping.
- Add whole numbers with regrouping.
- Find the perimeter of a polygon.
- Solve application problems using addition.
Introduction
Adding is used to find the total number of two or more quantities. The total is called the sumThe result when two or more numbers are added; the quantity that results from addition., or the number that results from the addition. You use addition to find the total distance that you travel if the first distance is `1,240` miles and the second distance is `530` miles. The two numbers to be added, `1,240` and `530`, are called the addendsA number added to one or more numbers to form a sum. . The total distance, `1,770` miles, is the sum.
Adding Whole Numbers without Regrouping
Adding numbers with more than one digit requires an understanding of place valueThe value of a digit based on its position within a number. . The place value of a digit is the value based on its position within the number. In the number `492`, the `4` is in the hundreds place, the `9` is in the tens place, and the `2` is in the ones place. You can use a number line to add. In the example below, the blue lines represent the two quantities, `15` and `4`, that are being added together. The red line represents the resulting quantity.
|
Example
|
|
Problem
|
`15 + 4=text()?`
|
|

|
|
On the number line, the blue line segment stretches across `15` units, representing the number `15`. The second blue segment shows that if you add `4` more units, the resulting number is `19`.
|
|
Answer
|
`15 + 4 = 19`
|
| |
|
|
You can solve the same problem without a number line, by adding vertically. When adding numbers with more than `1` digit, it is important to line up your numbers by place value, as in the example below. You must add ones to ones, tens to tens, hundreds to hundreds, and so on.
|
|
Example
|
|
Problem
|
`15 + 4=text()?`
|
|
|
|
|
|
|
|
Because `5` and `4` have the same place value, make sure they are aligned when you add.
|
|
|
|
First, add the ones digits (the numbers on the right). The result goes in the ones place for the answer.
|
|
|
|
Then, add the tens digits and put the result in the tens place of the answer. In this case, there is no tens digit in the second number, so the result is the same as the tens digit of the first number (`1`).
|
|
|
Answer
|
`15 + 4 = 19`
|
| |
|
|
|
|
|
|
This strategy of lining up the numbers is effective for adding a series of numbers as well.
|
Example
|
|
Problem
|
`1 + 2 + 3 + 2=text()?`
|
|
|
|
|
Answer `1 + 2 + 3 + 2 = 8`
|
Adding Whole Numbers with Regrouping
When adding whole numbers, a place-value position can have only one digit in it. If the sum of digits in a place value position is more than `10`, you have to regroupRewriting a number so you can subtract a greater digit from a lesser digit. the number of tens to the next greater place value position.
When you add, make sure you line up the digits according to their place values, as in the example below. As you regroup, place the regrouped digit above the appropriate digit in the next higher place value position and add it to the numbers below it.
|
Example
|
|
Problem
|
`45 + 15=text()?`
|
|
|
| |
`1` |
|
| |
`4` |
`5` |
| `+` |
`1` |
`5` |
| |
`6` |
`0` |
|
Add the ones. Regroup as needed. The sum of `5` and `5` is `10`. This is `1` ten and `0` ones. Write the number of ones (`0`) in the ones place and the `1` ten in the tens place above the `4`.
Add the tens, `1 + 4 + 1` is `6` tens. The final sum is `60`.
|
|
Answer
|
`45+15=60`
|
You must add digits in the ones place first, the digits in the tens place next, and so on. Go from right to left.
|
Example
|
|
Problem
|
`4,576 + 698=text()?`
|
| |
|
|
|
|
| |
`4,` |
`5` |
`7` |
`6` |
| `+` |
|
`6` |
`9` |
`8` |
| |
|
|
|
|
| |
|
|
`1` |
|
| |
`4,` |
`5` |
`7` |
`6` |
| `+` |
|
`6` |
`9` |
`8` |
| |
|
|
|
`4` |
| |
|
`1` |
`1` |
|
| |
`4,` |
`5` |
`7` |
`6` |
| `+` |
|
`6` |
`9` |
`8` |
| |
|
|
`7` |
`4` |
| |
`1` |
`1` |
`1` |
|
| |
`4,` |
`5` |
`7` |
`6` |
| `+` |
|
`6` |
`9` |
`8` |
| |
|
`2` |
`7` |
`4` |
| |
`1` |
`1` |
`1` |
|
| |
`4,` |
`5` |
`7` |
`6` |
| `+` |
|
`6` |
`9` |
`8` |
| |
`5,` |
`2` |
`7` |
`4` |
|
First, write the problem with one addend on top of the other. Be sure you line up the place values!
Add the numbers, `6` and `8`, in the ones place. Since the sum is `14`, write the ones value (`4`) in the ones place of the answer. Write the `1` ten in the tens place above the `7`.
Add the numbers in the tens place. Since the sum is `17` tens, regroup `17` tens as `1` hundred, `7` tens. Write `7` in the tens place in the answer and write the `1` hundred in the hundreds place above the `5`.
Add the numbers in the hundreds place, including the `1`. Again, the sum is more than one digit. Rename `12` hundreds as `2` hundreds and `1` thousand. Write the `2` in the hundreds place and the `1` above the `4` in the thousands place.
Add the numbers in the thousands place, including the `1`. The final sum is `5,274`.
|
|
Answer
|
`4,576 + 698 = 5,274`
|
| |
|
|
Adding Numbers Using the Partial Sums Method
Another way to add is the partial sums method. In the example below, the sum of `23 + 46` is found using the partial sums method. In this method, you add together all the numbers with the same place value and record their values (not just a single digit). Once you have done this for each place value, add their sums together.
|
Example
|
|
Problem
|
`23 + 46=text()?`
|
|
|
Step `1`: Add Tens
|
|
| |
`23` |
|
`20` |
| |
`46` |
`+` |
`40` |
| |
|
|
`60` |
|
|
|
|
Let’s begin by adding the values in the tens position, the `2` and `4`. The values are written as `20` and `40`.
|
|
Step `2`: Add Ones
|
|
|
| |
`23` |
|
`3` |
| |
`46` |
`+` |
`6` |
| |
|
|
`9` |
|
|
|
|
|
|
Add the values in the ones place, the `3` and `6`.
|
|
Step `3`: Add Parts
|
Finally, add the two sums, `60` and `9`, together.
|
|
Answer
|
`23 + 46 = 69`
|
| |
|
|
|
The next example adds a series of three numbers. Notice that hundreds is the greatest place value now, so hundreds are added before the tens. (You can add in any order that you prefer.) Also notice that in Step `3`, the value in the ones column for `350` is zero, but you still add that in to make sure everything is accounted for.
|
Example
|
|
Problem
|
`225 + 169 + 350=text()?`
|
|
|
Step `1`: Add Hundreds
|
|
|
| `2` |
`2` |
`5` |
|
|
`200` |
| `1` |
`6` |
`9` |
|
|
`100` |
| `3` |
`5` |
`0` |
|
`+` |
`300` |
| |
|
|
|
|
`600` |
|
|
|
|
|
Add the values represented by the digits `2`, `1`, and `3` in the hundreds place first. This gives a sum of `600`.
|
|
Step `2`: Add Tens
| `2` |
`2` |
`5` |
|
|
`20` |
| `1` |
`6` |
`9` |
|
|
`60` |
| `3` |
`5` |
`0` |
|
`+` |
`50` |
| |
|
|
|
|
`130` |
|
|
|
|
|
| |
|
|
|
|
Next, add the values from the digits in the tens place, the `2`, `6`, and `9`. The sum is `130`.
|
|
Step `3`: Add Ones
|
|
|
| `2` |
`2` |
`5` |
|
|
`5` |
| `1` |
`6` |
`9` |
|
|
`9` |
| `3` |
`5` |
`0` |
|
`+` |
`0` |
| |
|
|
|
|
`14` |
|
|
|
|
| |
|
|
|
Add the values from the digits in the ones place, the `5`, `9`, and `0`. The sum is `14`.
|
|
Step `4`: Add Parts
|
| |
|
|
|
`600` |
| |
|
|
|
`130` |
| |
|
|
`+` |
`14` |
| |
|
|
|
`744` |
|
|
|
|
|
At this point, you have a sum for each place value. Add together these three sums, which gives a final value of `744`.
|
|
Answer
|
`225 +169+350=744`
|
|
A local company built a playground at a park. It took the company `124` hours to plan out the playground, `243` hours to prepare the site, and `575` hours to build the playground. Find the total number of hours the company spent on the project.
A) `937` hours
B) `812` hours
C) `742` hours
D) `942` hours
A) `937` hours
Incorrect. You probably did not add the ones correctly. The correct answer is `942` hours.
B) `812` hours
Incorrect. You probably did not add the tens correctly. The correct answer is `942` hours.
C) `742` hours
Incorrect. You probably did not add the hundreds correctly. The correct answer is `942` hours.
D) `942` hours
Correct. You carried out the partial sums process effectively. The parts should be `800 + 130 + 12`.
|
When adding multi-digit numbers, use the partial sums method or any method that works best for you.
Finding the Perimeter of a Polygon
A polygonA closed plane figure bounded by three or more line segments. is a many-sided closed figure with sides that are straight line segments. Triangles, rectangles, and pentagons (five-sided figures) are polygons, but a circle or semicircle is not. The perimeterThe distance around a two-dimensional shape. of a polygon is the distance around the polygon. To find the perimeter of a polygon, add the lengths of its sides, as in the example below.
|
Example
|
|
Problem
|
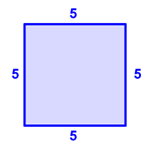
One side of a square has a length of `5` cm. Find the perimeter.
|
|
|
Draw the polygon and label the lengths of the sides. Since the side lengths of a square are equal, each side is `5` cm.
|
|
Answer The perimeter is `20` cm.
|
Add the lengths of each side, `5+5+5+5`.
|
The key part of completing a polygon problem is correctly identifying the side lengths. Once you know the side lengths, you add them as you would in any other addition problem.
|
Example
|
|
Problem
|
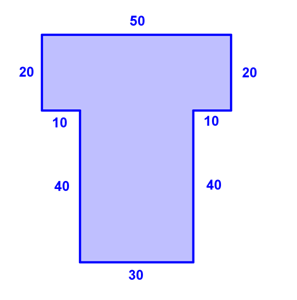
A company is planning to construct a building. Below is a diagram illustrating the shape of the building’s floor plan. The length of each side is given in the diagram. Measurements for each side are in feet. Find the perimeter of the building.
|
|
| |
`50` |
| |
`20` |
| |
`20` |
| |
`10` |
| |
`10` |
| |
`40` |
| |
`40` |
| `+` |
`30` |
| |
`220` |
|
Add the lengths of each side, making sure to align all numbers according to place value.
|
|
Answer The perimeter is `220` feet.
|
| |
|
|
|
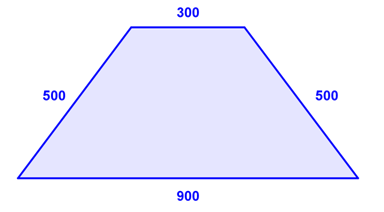
Find the perimeter of the trapezoid in feet.
a) `2,200` feet
b) `1,200` feet
c) `200` feet
d) `3,200` feet
A) `2,200` feet
Correct. You added the lengths of the sides together successfully.
B) `1,200` feet
Incorrect. You probably did not add the two diagonal sides of the trapezoid. The correct answer is `2,200` feet.
C) `200`
Incorrect. You probably subtracted the total length of the two sides, `1,000` feet, from the total length of the top and bottom, `1,200`. The correct answer is `2,200` feet.
D) `3,200` feet
Incorrect. You may have added some of the sides more than once. The correct answer is `2,200` feet.
|
Solving Application Problems
Addition is useful for many kinds of problems. When you see a problem written in words, look for key words that let you know you need to add numbers.
|
Example
|
|
Problem
|
A woman preparing an outdoor market is setting up a stand with `321` papayas, `45` peaches, and `213` mangos. How many pieces of fruit in total does the woman have on her stand?
|
|
|
The words “how many… in total” suggest that you need to add the numbers of the different kinds of fruits.
Use any method you like to add the numbers. Below, the partial sums method is used.
|
|
Step `1`: Add Hundreds
| `3` |
`2` |
`1` |
|
|
`300` |
| `0` |
`4` |
`5` |
|
|
`0` |
| `2` |
`1` |
`3` |
|
`+` |
`200` |
| |
|
|
|
|
`500` |
|
Step `2`: Add Tens
| `3` |
`2` |
`1` |
|
|
`20` |
| `0` |
`4` |
`5` |
|
|
`40` |
| `2` |
`1` |
`3` |
|
`+` |
`10` |
| |
|
|
|
|
`70` |
|
Step `3`: Add Ones
| `3` |
`2` |
`1` |
|
|
`1` |
| `0` |
`4` |
`5` |
|
|
`5` |
| `2` |
`1` |
`3` |
|
`+` |
`3` |
| |
|
|
|
|
`9` |
|
|
|
Step `4`: Add Parts
|
Add the numbers represented by the digits in the hundreds place first, the `3, 0`, and `2`. This gives a sum of `500`.
Next, add the numbers represented by the digits from the tens place, the `2, 4`, and `1`. The sum is `70`.
Add the numbers from the ones, the `1, 5`, and `3`.
Add together the three previous sums. The final sum is `579`.
|
|
Answer The woman has `579` pieces of fruit on her stand.
|
| |
|
|
|
Example
|
|
Problem
|
Lynn has `23` rock CDs, `14` classical music CDs, `8` country and western CDs, and `6` movie soundtrack CDs. How many CDs does she have in all?
|
|
|
The words “how many… in all” suggest that addition is the way to solve this problem.
To find how many CDs Lynn has, you need to add the number of CDs she has for each music style.
|
| |
`2` |
| |
`23` |
| |
`14` |
| |
`8` |
| `+` |
`6` |
| |
`51` |
|
Use whatever method you prefer to find the sum of the numbers.
|
|
|
|
|
Answer
|
Lynn has `51` CDs.
|
| |
|
|
The following phrases also appear in problem situations that require addition.
|
Phrase
|
Example problem
|
|
Add to
|
Jonah was planning a trip from Boston to New York City. The distance is `218` miles. His sister wanted him to visit her in Springfield, Massachusetts, on his way. Jonah knew this would add `17` miles to his trip. How long is his trip if he visits his sister?
|
|
Plus
|
Carrie rented a DVD and returned it one day late. The store charged `$5` for a two-day rental, plus a `$3` late fee. How much did Carrie pay for the rental?
|
|
Increased by
|
One statistic that is important for football players in offensive positions is rushing. After four games, one player had rushed `736` yards. After two more games, the number of yards rushed by this player increased by `352` yards. How many yards had he rushed after the six games?
|
|
More than
|
Lavonda posted `38` photos to her social network profile. Chris posted `27` more photos to his than Lavonda. How many photos did Chris post?
|
|
Example
|
|
Problem
|
Lena was planning a trip from her home in Amherst to the Museum of Science in Boston. The trip is `91` miles. She had to take a detour on the way, which added `13` miles to her trip. What is the total distance she traveled?
|
|
The word “added” suggests that addition is the way to solve this problem.
To find the total distance, you need to add the two distances.
|
|
Answer The total distance is `104` miles.
|
It can help to seek out words in a problem that imply what operation to use. See if you can find the key word(s) in the following problem that provide you clues on how to solve it.
|
A city was struck by an outbreak of a new flu strain in December. To prevent another outbreak, `3,462` people were vaccinated against the new strain in January. In February, `1,298` additional people were vaccinated. How many people in total received vaccinations over these two months?
a) `2,164`
b) `4,760`
c) `4,660`
d) `4,750`
A) `2,164`
Incorrect. You probably subtracted instead of adding. The correct answer is `4,760`.
B) `4,760`
Correct. You recognized this as an addition problem and successfully carried out your addition process.
C) `4,660`
Incorrect. You probably did not regroup to the hundreds place, or added the hundreds places incorrectly. The correct answer is `4,760`.
D) `4,750`
Incorrect. You probably did not regroup to the tens place, or added the tens place incorrectly. The correct answer is `4,760`.
|
Drawing a diagram to solve problems is very useful in fields such as engineering, sports, and architecture.
|
Example
|
|
Problem
|
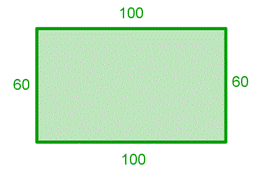
A coach tells her athletes to run one lap around a soccer field. The length of the soccer field is `100` yards, while the width of the field is `60` yards. Find the total distance that each athlete will have run after completing one lap around the perimeter of the field.
|
|
|
The words “total distance” and “perimeter” both tell you to add.
Draw the soccer field and label the various sides so you can see the numbers you are working with to find the perimeter.
|
|
| |
`1` |
|
|
| |
`1` |
`0` |
`0` |
| |
`1` |
`0` |
`0` |
| |
|
`6` |
`0` |
| `+` |
|
`6` |
`0` |
| |
|
`2` |
`0` |
| |
`1` |
|
|
| |
`1` |
`0` |
`0` |
| |
`1` |
`0` |
`0` |
| |
|
`6` |
`0` |
| `+` |
|
`6` |
`0` |
| |
`3` |
`2` |
`0` |
|
There is a zero in the ones place, and the sum of `6` and `6` in the tens place is `12` tens. Place `2` tens in the tens place in the answer, and regroup `10` tens as `1` hundred.
By adding the `1` hundred to the other digits in the hundreds place, you end up with a `3` in the hundreds place of the answer.
|
|
Answer Each athlete will have run `320` yards.
|
| |
|
|
Summary
You can add numbers with more than one digit using any method, including the partial sums method. Sometimes when adding, you may need to regroup to the next greater place value position. Regrouping involves grouping ones into groups of tens, grouping tens into groups of hundreds, and so on. The perimeter of a polygon is found by adding the lengths of each of its sides.




