Rounding Whole Numbers
In some situations, you don’t need an exact answer. In these cases, roundingFinding a number that’s close to a given number, but is easier to think about. the number to a specific place valueThe value of a digit based on its position within a number. is possible. For example, if you travelled `973` miles, you might want to round the distance to `1,000` miles, which is easier to think about. Rounding also comes in handy to see if a calculation is reasonable.
These are the rules for rounding whole numbersAny of the numbers `0`, `1`, `2`, `3`, and so on. :
First, identify the digit with the place value to which you are rounding. You might circle or highlight the digit so you can focus on it better.
Then, determine the possible numbers that you would obtain by rounding. These possible numbers are close to the number that you’re rounding to, but have zeros in the digits to the right.
If you are rounding `186` to the nearest ten, then `180` and `190` are the two possible numbers to round to, as `186` is between `180` and `190`. But how do you know whether to round to `180` or `190`?
|
Usually, round a number to the number that is closest to the original number.
When a number is halfway between the two possible numbers, round up to the greater number.
|
Since `186` is between `180` and `190`, and `186` is closer to `190`, you round up to `190`.
You can use a number line to help you round numbers.
|
Example |
||
|
Problem
|
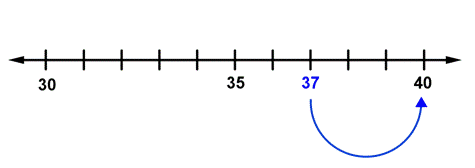
A camera is dropped out of a boat, and sinks to the bottom of a pond that is `37` feet deep. Round `37` to the nearest ten. |
|
|
`37`
|
The digit you’re rounding to is the tens digit, `3`. |
|
|
`30`...`37`...`40` |
`37` is between `30` and `40`. |
|
|
|
`37` is only `3` away from `40`, but it’s `7` away from `30`. So, `37` is closer to `40`. |
|
|
Answer To the nearest ten, `37` rounds to `40`. |
||
|
Example |
||
|
Problem |
Round `33` to the nearest ten. |
|
|
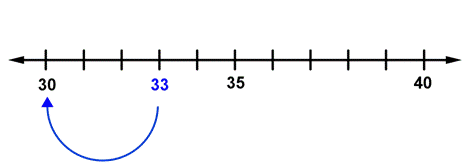
`33` rounds to `30` because `33` is closer to `30`.
|
||
|
Answer |
To the nearest ten, `33` rounds to `30`. |
|
You can determine where to round without using a number line by looking at the digit to the right of the one you’re rounding to. If that digit is less than `5`, round down. If it’s `5` or greater, round up. In the example above, you can see without a number line that `33` is rounded to `30` because the ones digit, `3`, is less than `5`.
|
Example |
||
|
Problem |
Round `77` to the nearest ten. |
|
|
`77` rounds to `80` because the ones digit, `7`, is `5` or greater.
|
||
|
Answer |
`77` rounded to the nearest ten is `80`. |
|
|
Example |
||
|
Problem
|
There are `576` jellybeans in a jar. Round this number to the nearest ten. |
|
|
`576` rounds to `580` because the ones digit, `6`, is `5` or greater.
|
||
|
Answer |
`576` rounded to the nearest ten is `580`. |
|
In the previous examples, you rounded to the tens place. The rounded numbers had a `0` in the ones place. If you round to the nearest hundred, the rounded number will have zeros in the tens and ones places. The rounded number will resemble `100`, `500`, or `1,200`.
|
Example |
||
|
Problem
|
A runner ran `1,539` meters, but describes the distance he ran with a rounded number. Round `1,539` to the nearest hundred. |
|
|
`1,539` rounds to `1,500` because the next digit is less than `5`.
|
||
|
Answer |
`1,539` rounded to the nearest hundred is `1,500`. |
|
If you round to the nearest thousand, the rounded number will have zeros in the hundreds, tens, and ones places. The rounded number will resemble `1,000`, `2,000`, or `14,000`.
|
Example |
|
|
Problem
|
A plane’s altitude increased by `2,721` feet. Round this number to the nearest thousand. |
|
`2,721` rounds to `3,000` because the next digit, `7`, is `5` or greater.
|
|
|
Answer `2,721` rounded to the nearest thousand is `3,000`. |
|
Now that you know how to round to the nearest ten, hundred, and thousand, try rounding to the nearest ten thousand.
|
Example |
||
|
Problem |
Round `326,749` to the nearest ten thousand. |
|
|
`326,749` rounds to `330,000` because the next digit, `6`, is `5` or greater.
|
||
|
Answer |
`326,749` rounded to the nearest ten thousand is `330,000`. |
|
|
A record number of `23,386` people voted in a city election. Round this number to the nearest hundred.
A) `23,300`
B) `23,400`
C) `23,000`
D) `23,390`
|
In situations when you don’t need an exact answer, you can round numbers. When you round numbers, you are always rounding to a particular place value, such as the nearest thousand or the nearest ten. Whether you round up or round down usually depends on which number is closest to your original number. When a number is halfway between the two possible numbers, round up to the larger number.
