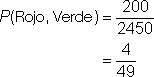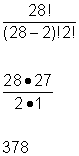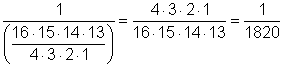Probabilidad y Eventos Dependientes
Objetivo de Aprendizaje
· Calcular la probabilidad de eventos dependientes.
Introducción
La probabilidad de cualquier tipo de evento — simple, compuesto, independiente, dependiente — siempre sigue la misma fórmula básica:
![]()
La probabilidad es la razón entre los tamaños de los espacios de eventos y muestral. Para algunas situaciones, como eventos dependientes e independientes, existen maneras de calcular estos números sin tener que pasar por el proceso de encontrar y contar los resultados posibles uno por uno, lo que es a veces tedioso y propenso a errores.
Para encontrar la probabilidad de eventos dependientes, podemos usar la Principio Fundamental de Conteo o las fórmulas factoriales de las permutaciones y las combinaciones para encontrar los tamaños de los espacios de eventos y muestral.
| El Principio Fundamental de Conteo encuentra el número de permutaciones y combinaciones de la siguiente manera:
Cuando se escogen k de n objetos, el número de permutaciones es
Cuando se escogen k de n objetos, el número de combinaciones es
Las fórmulas factoriales calculan permutaciones y combinaciones de esta manera:
Cuando se escogen k de n objetos, el número de permutaciones es
Cuando se escogen k de n objetos, el número de combinaciones es
|
Encontrar el espacio de eventos normalmente requiere un poco de reflexión e imaginación para identificar todas las maneras en las que un evento puede suceder.
| Ejemplo |
| ||||
| Problema | Sacas una canica de una bolsa con 20 canicas rojas, 20 blancas, y 10 verdes. Te quedas con la canica y sacas otra. ¿Cuál es la probabilidad de sacar una canica roja y luego sacar una canica verde? |
| |||
|
|
permutación |
| Queremos sacar primero una canica roja y luego una canica verde, entonces el orden importa. Este es un problema de permutaciones | ||
|
|
espacio muestral = 2450 |
| El tamaño del espacio muestral es el número de todas las permutaciones posibles de 2 canicas. La fórmula factorial para esto es | ||
|
|
Rojo, Verde |
| El tamaño del espacio de eventos es el número de todas las posibles combinaciones para las cuales la primera canica es roja y la segunda es verde | ||
|
|
20 • 10
espacio de eventos = 200
|
| ¿Cuántas maneras hay de que esto pase? ¡No cometas el error de creer que sólo hay una: roja y verde! Hay 20 canicas rojas diferentes que pueden ser escogidas al principio. Luego hay 10 canicas verdes diferentes para escoger después. El Principio Fundamental de Conteo dice que multipliquemos estas para obtener el número de formas de sacar rojo y luego verde | ||
|
|
|
| Ahora la probabilidad de sacar roja y verde es la razón de todas las maneras de sacar esos dos colores en ese orden con todas las permutaciones posibles | ||
| Solución | La probabilidad de que salgan canicas roja y verde es |
| |||
Cuando buscamos un espacio de eventos, a veces es útil pensar en el evento que queremos como eliminando resultados particulares de eventos individuales. Luego tenemos que encontrar el número de permutaciones o combinaciones para el resto de los resultados. En el ejemplo anterior de las canicas, eliminado reojo para la primera sacada no cambió el número de canicas verdes que quedaban disponibles. Sin embargo, si queríamos la probabilidad de sacar una roja y luego otra rojo, existen 20 • 19 maneras de hacerlo cuando el orden importa.
Veamos el siguiente ejemplo que implica combinaciones
| Ejemplo |
| ||||
| Problema | Una organización de una escuela tiene 30 miembros. Cuatro miembros serán escogidos al azar para una entrevista con el periódico de la escuela sobre el grupo. ¿Cuál es la probabilidad de que Tom y Cindy sean escogidos? |
|
| ||
|
|
combinación |
| No hay razón por la que una persona se considere diferente a otra, basados en el orden en que son escogidas, entonces los espacios de eventos y muestral involucran combinaciones y no permutaciones |
| |
|
|
|
| El tamaño del espacio muestral es el número de todas las posibles combinaciones de 4 miembros. La fórmula para las combinaciones es | ||
|
|
|
| El tamaño del espacio de eventos es el número de todas las combinaciones posibles que incluyen a Tom y Cindy. |
| |
|
|
Tom, Cindy, __?__, __?__
Encontrar otras 2 personas de las 28 restantes.
|
| Si Tom y Cindy deben ser escogidos, entonces ya conocemos a 2 de nuestras 4 personas. Ahora el problema es ¿cómo podemos llenar esos 2 espacios con los otros 28 miembros? Este es un nuevo problema de combinaciones, escogiendo 2 de 28 miembros. |
| |
|
|
|
| Para usar la fórmula, sea n = 28 y k = 2. |
| |
|
|
|
| Ahora la probabilidad de que Tom y Cindy sean escogidos es la razón entre las combinaciones que los incluyen y todas las posibles combinaciones |
| |
| Solución | La probabilidad de que Tom y Cindy sean escogidos es |
|
|
| |
Este es un pequeño consejo de aritmética: podría ser más fácil simplificar la fracción de probabilidad dejando los tamaños muestral y de eventos en su forma factorizada. Por ejemplo:
![]()
Dividimos fracciones invirtiendo el divisor y multiplicando. Luego podemos eliminar factores comunes en el numerador y en el denominador:
![]()
![]()
![]()
![]()
| Una bolsa de canicas tiene 20 canicas rojas, 20 blancas, y 10 verdes. Si sacamos tres canicas, ¿cuál es la probabilidad de que saquemos exactamente dos canicas rojas?
A)
B)
C)
D)
|
Probabilidades de Eventos Dependientes e Independientes
Hemos estado usando el Principio Fundamental de Conteo y las fórmulas de permutación y combinación para calcular la probabilidad de una serie de eventos en su conjunto. También podemos calcular la probabilidad de un evento a la vez. Podemos usar la siguiente regla para calcular la probabilidad de eventos independientes:
| Si A y B son eventos independientes, P(A y B) = P(A) • P(B).
En general, para cualquier número independiente de eventos, la probabilidad de que todos los eventos sucedan es el producto de las probabilidades de que los eventos individuales sucedan. |
Entonces podemos encontrar la probabilidad de muchos eventos independientes encontrando la probabilidad de cada evento independiente, y luego multiplicándolas todas. Cada evento individual tendría la misma probabilidad incluso si ninguno de los otros eventos ocurre.
La probabilidad de eventos dependientes puede ser encontrada de una forma casi igual. Considera algunos de los eventos dependientes con los que hemos estado trabajando, como el ejemplo de las canicas. La probabilidad para ese ejemplo también implicaba productos.
![]()
Si vemos esto como tres eventos separados, ¿cuáles son las probabilidades individuales?
Primera sacada: ![]()
Segunda sacada: ![]()
Tercera sacada: ![]()
Nota el producto de estas probabilidades individuales:
![]()
¡Es el mismo resultado! Entonces somos capaces de calcular la probabilidad de una serie de eventos dependientes encontrando la probabilidad de cada evento individual y luego multiplicándolas juntas. Pero, las probabilidades individuales no son las mismas que si los eventos ocurrieran solos, como sería el caso con los eventos independientes. Con los eventos dependientes, las probabilidades de eventos posteriores son diferentes a las que serían si hubieran ocurrido por sí solos.
| Si A y B son eventos dependientes, P(A y B) = P(A) • P(B después A) donde P(B después A) es la probabilidad de que ocurra B después de que A haya ocurrido.
En general, para cualquier número de eventos independientes, la probabilidad de que todos los eventos sucedan es el producto de las probabilidades de que sucedan los eventos individuales, siempre y cuando la ocurrencia de un evento anterior sea incluida cuando se encuentran las probabilidades de eventos posteriores. |
Probemos este método con un problema:
| Ejemplo | ||||
| Problema | Te has sentado accidentalmente en tu teléfono celular, y cada vez que te mueves, se marcan número diferentes en tu agenda. Tienes guardados 16 números, y llamas a 4 de ellos antes de pararte. ¿Cuál es la probabilidad de que Mary, Lulu, Bo, y Dan hayan recibido una llamas? |
| ||
|
| Mary recibió una llamada Lulu recibió una llamada Bo recibió una llamada Dan recibió una llamada |
| Primero definiremos los eventos individuales. El orden no importa | |
|
|
|
| Ahora encontremos la probabilidad de cada evento. Para la primera llamada, hay 4 números en el espacio de eventos y 16 números de donde escoger, Si la primera llamada es para Mary, Lulu, Bo, o Dan, para la segunda llamada habrá 3 posibilidades de llamar a alguien en el evento y 15 números restantes que podrían ser llamados. Para la tercera llamada, habría 2 opciones de 14 números, y luego sólo 1 de 13 números para la última llamada.
Usa estos números para encontrar las probabilidades de cada llamada. | |
|
|
|
| La probabilidad de que los cuatro eventos ocurran es el producto de las probabilidades individuales. | |
|
|
|
| Encontremos de nuevo la probabilidad usando la fórmula de las combinaciones. Queremos una combinación porque el orden no importa | |
|
|
|
| El espacio muestral es el número de combinaciones de 4 teléfonos de 16. Aquí, k = 4 y n = 16. | |
|
|
|
| El espacio de eventos es el número de combinaciones para escoger 4 de 4 teléfonos. Hay sólo una forma de hacer eso — ¡los 4 son llamados! Podemos probar esto con la fórmula (recuerda que 0! = 1). | |
|
|
|
| La probabilidad es la razón de los tamaños del evento y la muestra
Nota que el resultado es el mismo que obtuvimos calculando individualmente | |
| Solución |
|
|
| |
| Un grupo de 8 amigos están jugando un juego de mesa en el que los jugadores compiten para llegar al último cuadro del tablero. Lo amigos van a reconocer al primer, segundo y tercer lugar.
Asumiendo que todos los jugadores tienen las mismas probabilidades de ganar, ¿cuál es la probabilidad de que Juanita quede en primer lugar, y que Bill o Susan quede en segundo y Bill o Susan quede en tercero?
A)
B)
C)
D)
|
Sumario
Existen varias formas de encontrar las probabilidades de eventos dependientes. La secuencia de eventos puede ser tratada como un todo, en ese caso el Principio Fundamental de Conteo o las fórmulas de permutaciones y combinaciones son usadas para encontrar los tamaños del espacio de eventos y el espacio muestral.
O cada evento puede ser tratado separadamente, don de las probabilidades de cada evento son multiplicadas para encontrar la probabilidad de toda la cadena de eventos:
Si A y B son eventos dependientes, P(A y B) = P(A) • P(B después A) donde P(B después A) es la probabilidad de que ocurra B después de que A haya ocurrido.
Sin importar el método, debemos notar que cuando los eventos son dependientes, el tamaño de los espacios muestral y de eventos pueden cambiar con el tiempo, porque la ocurrencia de un evento afecta los resultados de otros eventos.