Permutaciones y Combinaciones
Objetivo de Aprendizaje
· Usar el Principio Fundamental de Conteo para calcular permutaciones y combinaciones.
Introducción
Algunas situaciones de probabilidad implican múltiples eventos. Cuando uno de los eventos afecta a otros, se llaman eventos dependientes. Por ejemplo, cuando objetos son escogidos de una lista o grupo y no son devueltos, la primera elección reduce las opciones para futuras elecciones.
Existen dos maneras de ordenar o combinar resultados de eventos dependientes. Las permutaciones son agrupaciones en las que importa el orden de los objetos. Las combinaciones son agrupaciones en las que el contenido importa pero el orden no.
Eventos Dependientes
Dos eventos son dependientes si el estado original de la situación cambia de un evento al otro, y esto altera la probabilidad del segundo evento.
| Los eventos dependientes ocurren cuando una acción elimina un resultado posible, y el resultado no es devuelto antes de que suceda una segunda acción.
A esto se le llama elección sin devolución. |
Una forma de saber si eventos son dependientes o independientes es encontrar si un resultado eliminado es devuelto (haciéndolos independientes) o no devuelto (haciéndolos dependientes). Aquí hay algunos ejemplos.
| Situación | Eventos | Por qué los eventos son dependientes |
| En una fiesta, sacas cuatro papelitos con nombres de invitados para formar un equipo de 4 personas. ¿Cuál es la probabilidad de que John, Perna, Tosho, y Lee quedarán en el mismo equipo? | Sacar el nombre de John Sacar el nombre de Perna Sacar el nombre de Tosho Sacar el nombre de Lee | Una vez que sacas un nombre, no lo pones de nuevo en el conjunto de nombres de donde lo sacaste. Cada vez, hay un nombre menos en el espacio muestral, y (si el evento continúa ocurriendo) un nombre menos en el espacio de eventos. La probabilidad de que un evento suceda cambia con cada nueva sacada. |
| Sacas una canica de una bolsa con 2 canicas rojas, 2 blancas, y una verde. Te quedas la canica y luego sacas otra. ¿Cuál es la probabilidad de sacar una canica roja y luego sacar la canica verde? | La primera sacada es roja. La segunda sacada es verde. | Estos eventos son dependientes porque no devuelves la primera canica que sacaste. Quedan menos canicas en el espacio muestral, por lo que la probabilidad de sacar una canica verde es distinta para la segunda sacada que para la primera.
|
| Sacas dos cartas de un mazo estándar de 52 cartas. (En un mazo estándar, cada carta tiene un palo — corazones, picas, diamantes, o tréboles — y un rango — As, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jota, Reina y Rey. ¿Cuál es la probabilidad de que ambas cartas sean 2s? | Una carta es un 2. Otra carta es un 2. | Como se sacan 2 cartas, la probabilidad de que le primera sea 2 es diferente de la probabilidad de que la segunda sea 2. (Menos cartas de donde escoger resulta en un espacio muestral más pequeño.) |
| Beth tiene 10 pares de calcetines: 2 negros, 2 cafés, 3 blancos, 1 rojo, 1 azul, y 1 verde. Hoy quiere usar el par blanco, pero tiene prisa para llegar al trabajo, por lo que agarra un para al azar. Si no es blanco, lo tirar a la cama y saca otro. Elige el enunciado que mejor describe esta situación.
A) Los eventos son dependientes, porque Beth no elimina ninguno de los resultados. B) Los eventos son dependientes, porque el resultado eliminado es devuelto después de cada intento. C) Los eventos son dependientes, porque un resultado es eliminado en cada intento y no es devuelto.
|
Una cosa que sabemos sobre situaciones que implican eventos dependientes es que una acción elimina resultados posibles de acciones futuras. Hay otro factor importante que considera sobre los resultados de eventos dependientes: ¿Cómo están organizados? ¿Debemos hacer una lista, anotando el orden en que ocurren, o sólo los amontonamos juntos ignorando el orden?
Considera los tres ejemplos anteriores, y piensa si el orden importa:
| Situación | Eventos | ¿Importa el orden? |
| En una fiesta, sacas cuatro papelitos con nombres de invitados para formar un equipo de 4 personas. ¿Cuál es la probabilidad de que John, Perna, Tosho, y Lee quedarán en el mismo equipo? | Sacar el nombre de John Sacar el nombre de Perna Sacar el nombre de Tosho Sacar el nombre de Lee | El orden no importa. Esas cuatro personas estarán en el mismo equipo así saques a John, Perna, Tosho, y luego Lee, o Perna, Tosho, Lee, y al final John.
|
| Sacas una canica de una bolsa con 2 canicas rojas, 2 blancas, y una verde. Te quedas la canica y luego sacas otra. ¿Cuál es la probabilidad de sacar una canica roja y luego sacar la canica verde? | La primera sacada es roja. La segunda sacada es verde. | El orden es importante. Sacar una canica verde y luego una roja no es un resultado aceptable en esta situación
|
| Sacas dos cartas de un mazo estándar de 52 cartas. (En un mazo estándar, cada carta tiene un palo — corazones, picas, diamantes, o tréboles — y un rango — As, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jota, Reina, o Rey. ¿Cuál es la probabilidad de que ambas cartas sean 2s? | Una carta es un 2. Otra carta es un 2. | El orden no importa. El resultado se satisface ya sea que saques el 2 de corazones y el 2 de picas, o el 2 de picas y luego el 2 de corazones. |
En situaciones que crean grupos de objetos (como personas, canicas, o cartas), necesitamos saber si su orden importa o no. De lo contrario no podemos encontrar los espacios muestral y de eventos.
Considera el ejemplo del equipo. En el espacio muestral, el resultado John, Perna, Tosho, Lee es el mismo que el resultado Perna, Lee, John, Tosho — no hay diferencia entre los equipos creados, aunque los nombres de los miembros hayan sido mencionados en un orden distinto. Por otro lado, supongamos que la primera persona sacada debe ser la que lance un globo lleno de agua, la segunda tiene que atraparlo, la tercera es quien lo revienta (si aún sigue intacto), y la cuarta es quien trata de colectar el agua en un vaso. Si John es un lanzador terrible pero Perna es buena lanzando, sería mejor para el equipo que saliera Perna, Lee, John, Tosho (para que Perna lance a Lee) que John, Perna, Tosho, Lee (John lance a Perna). El orden importaría.
| Ejemplo | |||||||||||||||||||||||||||||||||||||||||||||||||
| Problema | Una bolsa contiene 5 canicas, de color blanco, rojo, azul, púrpura y verde. Encuentra el tamaño del espacio muestral si sacas dos canicas, sin devolverlas, de dos maneras: 1) El orden importa. 2) El orden no importa. |
| |||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| Enlistar las posibilidades de la primer sacada, usamos sólo las iniciales de los colores (como son todas distintas) | ||||||||||||||||||||||||||||||||||||||||||||||
|
|
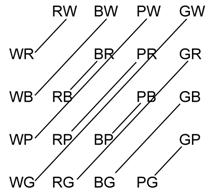
Espacio muestral (el orden importa): {RW, BW, PW, GW, WR, BR, PR, GR, WB, RB, PB, GB, WP, RP, BP, GP, WG, RG, BG, PG} |
| Ahora suma la segunda sacada. Como primero vamos a pensar cuando el orden importa, sólo añade la segunda sacada después de la primera. Recuerda que esto es sin reemplazo, por lo que no puedes repetir un color.
| ||||||||||||||||||||||||||||||||||||||||||||||
|
|
Espacio muestral (el orden no importa): {RW, BW, PW, GW, BR, PR, GR, PB, GB, GP} |
| Ahora, ¿cuál es la diferencia cuando el orden no importa? WR y RW son el mismo resultado, al igual que WB y BW, etc. En este diagrama, cada resultado está relacionado con su resultado equivalente. Como sólo necesitas uno de cada par, quedan la mitad de las soluciones | ||||||||||||||||||||||||||||||||||||||||||||||
| Solución |
Cuando el orden importa, el espacio muestral tiene 20 resultados. Cuando el orden no importa, el espacio muestral tiene 10 resultados. |
|
| ||||||||||||||||||||||||||||||||||||||||||||||
Cuando formamos grupos en los que el orden no importa, los grupos se llaman combinaciones. Cuando formamos grupos en los que el orden sí importa, los grupos se llaman permutaciones. Recuerda con permutaciones, posición (orden) importa.
Tamaño de Muestra y el Principio Fundamental de Conteo
Como la muestra y el tamaño del evento es lo que usamos para encontrar probabilidades, es útil saber exactamente cuántas combinaciones o permutaciones son posibles. Esta es una forma de pensar en ello, usando el Principio Fundamental de Conteo, que dice que el número de resultados en un espacio muestral es el producto del número de resultados para cada elemento.
Empecemos con las permutaciones, cuando el orden importa. Supongamos que tenemos n objetos de donde escoger (n canicas en la bolsa, o n invitados en una fiesta, por ejemplo).
· La primera sacada tiene una opción de n objetos
· Para cada uno de esos n objetos, existen n − 1 opciones para la segunda sacada. Usando el Principio Fundamental de Conteo, es significa que hay n • (n − 1) resultados para escoger dos cosas.
· Ahora, para esos n • (n − 1) resultados, se puede tener una tercera opción de los n − 2 objetos que restan. Usando de nuevo el Principio Fundamental de Conteo, hay n • (n − 1) • (n − 2) resultados posibles para 3 sacadas.
¿Ves a dónde va esto? Nota que el último factor resta uno menos que el número total de objetos elegidos. Para encontrar el número de opciones para sacar el k-ésimo objeto, multiplica los resultados anteriores por n − (k − 1). Otra forma de escribir n − (k − 1) es n − k + 1.
| Permutaciones Cuando elegimos k de n objetos y el orden importa, el número de permutaciones es
El símbolo "..." significa continuar de la misma manera. En este caso, significa que se continúe multiplicando por el siguiente número completo menor, por n – k + 1. |
Para las combinaciones, el orden no importa. ¿Cómo cambia esto el número de resultados? El número de permutaciones que se vuelven la misma cuando el orden ya no importa es el número de maneras distintas de arreglar objetos en un grupo.
Piensa en un grupo de 3 letras. ABC. En una permutación, ABC y CAB son resultados distintos, pero en una combinación, estos resultados son el mismo. ¿Cuántas maneras diferentes hay de ordenar las letras A, B, y C? Es decir, ¿cuántas permutaciones hay para este grupo en particular?
ABC ACB
BAC BCA
CAB CBA
Existen 6 maneras de ordenar estas letras. Lo que estamos haciendo es encontrando el número de permutaciones de 3 objetos cuando elegimos los 3 (n = 3 y k = 3). Entonces, usando la fórmula proporcionada arriba, existen 3 • 2 • 1 = 6 resultados. Que son los mismos que los resultados de la lista.
En el ejemplo de las canicas, teníamos 2 objetos en cada grupo, entonces para cada par de canicas, había 2 • 1, o 2, maneras de ordenarlas. Sólo necesitábamos una para cada par, por lo que el número de combinaciones ere el número de permutaciones dividido entre 2. En el ejemplo de las letras, como existen 6 maneras de ordenar 3 objetos, cuando encontramos las combinaciones de tres sólo necesitábamos una representativa para esas 6 formas. Podemos dividir el número de permutaciones entre 6 y obtener el número de combinaciones.
Esto es válido en general: Para encontrar el número de combinaciones de k objetos tomados de n objetos, dividir el número de permutaciones de escoger k de n objetos entre el número de permutaciones para escoger k de k objetos.
| Combinaciones
Cuando escogemos k de n objetos en un orden que no importa, el número de combinaciones es el número de permutaciones para k de n objetos dividido entre el número de permutaciones para escoger k de k objetos:
|
Tamaño de Muestra y Factoriales
Existe una forma más fácil de escribir fórmulas de permutaciones y combinaciones, usando una idea llamada factoriales. Un factorial es el producto de todos los números completos desde 1 hasta un número dado. El símbolo ! después de un número es usado para representar este producto, Por ejemplo, 3! = 3 • 2 • 1, y 7! = 7 • 6 • 5 • 4 • 3 • 2 • 1. Entonces, en general, n! = n • (n − 1) • … • 2 • 1. Nota especial: 0! se define como 1.
La fórmula del número de permutaciones empieza como n!, pero termina con (n − k + 1) en lugar de 1. Necesitamos eliminar los factores de (n − k) a 1 del producto. ¡Podemos hacer eso dividiendo entre (n − k)!
![]()
Entonces, para las combinaciones, dividimos el resultado entre k • (k − 1) • … • 2 • 1, o k.
| Usando Factoriales
Cuando escogemos k de n objetos, podemos usar las siguientes fórmulas:
Número de permutaciones =
Número de combinaciones =
|
Muchas calculadoras tienen la tecla o el comando factorial (!). Para encontrar el número de permutaciones de escoger 20 de 24 objetos, teclear 24! ÷ 4! es más rápido y fácil que 24 • 23 • 23 • 21 • 20 • 19 • 18 • 17 • 16 • 15 • 14 • 13 • 12 • 11 • 10 • 9 • 8 • 7 • 6 • 5. (Aunque, si sólo se hacen 4 elecciones, sería más fácil teclear 24 • 23 • 22 • 21.)
Probemos estas fórmulas en un problema. Primero, usaremos el Principio Fundamental de Conteo.
| Ejemplo | ||||||
| Problema | Una organización de una escuela tiene 30 miembros. Cuatro miembros serán escogidos al azar para una entrevista con el periódico de la escuela sobre el grupo. ¿Cuántos grupos de 4 personas son posibles? |
| ||||
|
|
combinación |
| Primero decidir si esta situación es una permutación o una combinación
No existe ninguna razón para que una persona sea considerada distinta de otra, por lo que esto es una combinación. | |||
|
|
|
| Existen 30 posibilidades para la primera sacada. Luego 29 posibilidades para la segunda persona, 28 para la tercera, y 27 para la cuarta. El Principio Fundamental de Conteo dice que debemos multiplicar estos resultados para obtener el número de posibilidades | |||
|
|
|
| Sin embargo, ese producto nos da el número de permutaciones, cuando el orden importa. Necesitamos tomar todos los posibles arreglos de 4 personas en particular y usar sólo una representación de cada uno.
Para cuatro personas, existen 4 opciones para enlistar a la primera, 3 para la segunda, 2 para la tercera, y sólo 1 opción para la cuarta. El Principio Fundamental de Conteo nos dice cuántas veces un grupo de 4 personas aparecerá en la lista de permutaciones
Dividir entre el producto que resulta del Principio Fundamental de Conteo | |||
| Solución | ¡Existen 27,405 posibles grupos diferentes de 4 personas a partir de 30 miembros! |
|
| |||
Ahora resolveremos el mismo problema con la fórmula factorial:
| Ejemplo | ||||
| Problema | Una organización de una escuela tiene 30 miembros. Cuatro miembros serán escogidos al azar para una entrevista con el periódico de la escuela sobre el grupo. ¿Cuántos grupos de 4 personas son posibles? |
| ||
|
|
combinación |
| Primero decidir si esta situación es una permutación o una combinación
No existe ninguna razón para que una persona sea considerada distinta de otra, por lo que esto es una combinación. | |
|
|
|
| La fórmula factorial para las combinaciones es
En este caso, estamos escogiendo 4 de 30 miembros, entonces n = 30 y k = 4. | |
| Solución | ¡Existen 27,405 posibles grupos diferentes de 4 personas a partir de 30 miembros! |
|
| |
Ambos métodos producen la misma respuesta.
| Un grupo de 8 amigos están jugando un juego de mesa en el cual los jugadores compiten para llegar primero a la última casilla de un tablero. Los amigos van a reconocer al primer, segundo y tercer lugar. ¿Cuántas maneras diferentes hay de que los 8 amigos tomen esos lugares?
A) 6 B) 56 C) 336 D) 40,320
|
Sumario
Dos (o más) eventos son dependientes si la probabilidad de un evento cambia cuando el éxito de otro evento es determinado. Esto pasa normalmente cuando una acción aleatoria para un evento elimina un resultado posible y el resultado no se devuelve antes de que suceda la acción del siguiente evento.
Para encontrar los espacios muestral y de eventos en estas situaciones, considera si los eventos implican permutaciones (el orden importa) o combinaciones (el orden no importa). Existen dos formas de calcular los espacios muestral y de eventos sin tener que enlistarlos todos, con el Principio Fundamental de Conteo y con fórmulas factoriales.
El Principio Fundamental de Conteo nos permite encontrar el número de permutaciones y combinaciones como sigue:
Cuando escogemos k de n objetos, el número de permutaciones es ![]()
![]()
Cuando escogemos k de n objetos, el número de combinaciones es ![]()
Las fórmulas factoriales calculan permutaciones y combinaciones de esta manera:
Cuando escogemos k de n objetos, el número de permutaciones = ![]()
Cuando escogemos k de n objetos, el número de combinaciones= ![]()