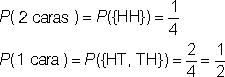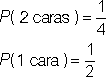Eventos y Resultados (Conteo)

 

Objetivos de Aprendizaje

·         Usar el Principio Fundamental de Conteo para determinar el tamaño del espacio de muestra para eventos simples y compuestos.

·         Determinar la probabilidad de eventos simples y compuestos.

 

 

Las situaciones aleatorias son aquellas que no se pueden predecir con certeza. Sin embargo, probabilidad, una medida de qué tan probable es que una situación aleatoria resultará de una manera particular, podemos ser capaces de hacer algunas predicciones sobre esas situaciones. Por ejemplo, muchos juegos usan dados o ruletas para generar números aleatoriamente. Si entendemos cómo calcular las probabilidades, podemos tomar decisiones informadas sobre cómo jugar esos juegos conociendo las probabilidades de varios resultados.

 

 

Primero necesitamos introducir algunos términos. Cuando trabajamos con probabilidad, una acción aleatoria o serie de acciones se llama experimento. Un resultado es la consecuencia de un experimento, y un evento es una colección particular de resultados. Los eventos usualmente son descritos usando una característica común de los resultados.

 

Apliquemos este lenguaje para ver cómo funcionan los términos en la práctica. Algunos juegos requieren lanzar un dado de seis lados, numerado del 1 al 6. La tabla siguiente ilustra el uso de experimento, resultado, y evento en ese juego:

 

 

Nota que una colección de resultados se pone en corchetes y separado por comas.

 

Un evento simple es un evento con un solo resultado. Sacar un 1 sería un evento simple, porque existe sólo un resultado que funciona: 1. Sacar más que 5 también sería un evento simple, porque el evento incluye sólo al 6 como un resultado válido. Un evento compuesto es un evento con más de un resultado. Por ejemplo, lanzar un dado de 6 lados y sacar un número par: 2, 4, y 6.

 

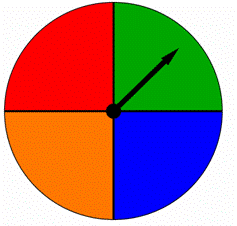
Cuando lanzamos muchas veces un dado de 6 lados, no debemos esperar que un resultado ocurra más frecuentemente que otro. Los resultados en esta situación se dice que son igualmente probables. Es muy importante reconocer cuándo los resultados son igualmente probables cuando calculamos probabilidades. Como cada resultado en el experimento de lanzar los dados es igualmente probable, esperaríamos obtener cada resultado  de los lanzamientos. Eso es, esperaríamos que salga 1 en  de los lanzamientos, 2 en  de los lanzamientos, 3 en  de los lanzamientos y así sucesivamente.

 

 

 

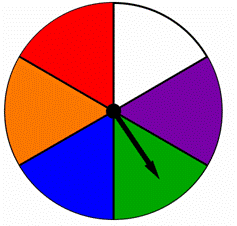
Cuando se gira esta ruleta, la flecha apunta a uno de los colores. ¿Son los resultados igualmente probables?     A) Sí, son igualmente probables. B) No, no son igualmente probables.   Mostrar/Ocultar la Respuesta Todos los resultados son igualmente probables. Cada color representa un resultado diferente, y cada color ocupa ¼ del círculo. Esperarías que la flecha apunte a cada color ¼ de las veces.

 

 

 

La probabilidad de un evento es la frecuencia con que se espera que ocurra. Cuando todos los resultados posibles de un experimento son igualmente probables, la probabilidad es la relación entre el tamaño del espacio de eventos (los resultados en el evento) y el espacio muestral (todos los posibles resultados del experimento). La probabilidad de un evento E normalmente se escribe P(E).

 

 

 

Nota que un evento es normalmente descrito usando características comunes de los resultados, si es posible — como lanzar un dado un número par de veces. El espacio de eventos, sin embargo, es una lista de todos los resultados en un evento — como {2, 4, 6}. El espacio muestral consiste de todos los resultados posibles, no sólo aquellos del evento.

 

 

 

Algunas veces los resultados no son igualmente probables. En este caso, necesitamos encontrar la manera de representar los resultados para que sean igualmente probables.

 

 

 

Es una práctica común en probabilidad, como en las fracciones en general, simplificar una probabilidad en sus términos más bajos para que sea más fácil tener ida de qué tan grande es. A menos que exista una razón para no hacerlo, expresaremos todas las probabilidades en sus términos más bajos.

 

Encontrar la probabilidad de que la ruleta saque azul o verde:       A)   B)   C) 2   D) 6   Mostrar/Ocultar la Respuesta A) Incorrecto. Hay 6 resultados igualmente probables, entonces la probabilidad de cada resultado es . Sin embargo, el evento tiene dos resultados en él, {azul, verde}. La probabilidad es . La respuesta correcta es .   B) Correcto. Hay 6 resultados igualmente probables, y el evento tiene dos resultados en él, {azul, verde}. La probabilidad es .   C) Incorrecto. Hay 2 resultados en el espacio de eventos, pero la probabilidad de un evento es la razón entre los resultados en el espacio de eventos y el número total de resultados igualmente probables. Hay 6 resultados igualmente probables, por lo que la probabilidad es .   D) Incorrecto. Hay 6 resultados igualmente probables en el espacio muestral, pero la probabilidad de un evento es la razón entre los resultados en el espacio de eventos y el número total de resultados igualmente probables. La probabilidad es .

 

 

Hasta ahora hemos visto experimentos con un número pequeño de resultados y eventos. Pero los experimentos y los eventos pueden hacerse complejos rápidamente. El siguiente ejemplo tiene mucho más resultados que los que hemos visto anteriormente:

 

 

 

Como hemos visto, cuando un experimento intervienen más de un elemento aleatorio, como lanzar más de una moneda o lanzar más de un dado, encontrar el espacio muestral de resultado igualmente probables puede ser complicado. Sin embargo, no necesitamos identificar cada resultado en el espacio muestral para calcular la probabilidad. Sólo necesitamos el número de resultados.

 

El Principio Fundamental de Conteo es una manera de encontrar el número de resultados sin tener que listar o contar cada uno de ellos.

 

El Principio Fundamental de Conteo   Cuando un experimento consiste en más de un elemento aleatorio, el número de resultados en el espacio muestral es igual al producto de el número de resultados para cada elemento aleatorio.   Ejemplos ·         Lanzar dos dados de 6 lados: Cada dado tiene 6 resultados igualmente probables, entonces el espacio muestral es 6 • 6 o 36 resultados igualmente probables. ·         Lanzar tres monedas: Cada moneda tiene 2 resultados igualmente probables, por lo que el espacio muestral es 2 • 2 • 2 u 8 resultados igualmente probables. ·         Lanzar un dado de 6 lados y una moneda: El espacio muestral es 6 • 2 o 12 resultados igualmente probables

 

El Principio Fundamental de Conteo también nos permite ver cuántas opciones existen cuando no estamos eligiendo aleatoriamente. Supón que en un ropero hay tres pares de pantalones (negro, blanco, y verde), cuatro camisas (verde, blanca, púrpura, y amarilla), y dos pares de zapatos (negro y blanco). ¿Cuántas combinaciones de vestimentas se pueden hacer? Existen 3 opciones de pantalones, 4 opciones de camisas, y 2 opciones de zapatos. El Principio Fundamental de Conteo dice que podemos hacer 4 • 3 • 2 o 24 combinaciones diferentes.

 

Veamos la respuesta por medio de un diagrama de árbol. Un diagrama de árbol tiene una rama por cada respuesta posible para cada evento. Para ahorrar espacio, usemos B para Negro, W para blanco, G para verde, P para púrpura, y Y para amarillo.

 

 

 

Observa por un momento el diagrama. Hay 3 opciones de pantalones. Para cada una, hay cuatro opciones de camisas. Eso significa que hay 3 • 4 combinaciones pantalón-camisa. Para cada una de esas 12 combinaciones, existen dos opciones de zapatos. Eso nos da 3 • 4 • 2 combinaciones de pantalón-camisa-zapato, entonces hay 24 posibles combinaciones para vestir.

 

Supongamos que escogemos pantalones, camisa, y zapatos de manera completamente aleatoria — es decir, hay la misma probabilidad de escoger cualquier pantalón, cualquier camisa, y cualquier par de zapatos. Existen 8 combinaciones de vestimenta en las cuales los pantalones y los zapatos son del mismo color (pantalones y zapatos negros y con cualquiera de las 4 camisas, o pantalones y zapatos blancos con cualquiera de las 4 camisas). La probabilidad de que los pantalones y los zapatos sean del mismo color será:

 

.

 

 

 

 

Carrie lanza cuatro monedas y cuenta el número de cruces (Tails). Hay 4 formas de obtener exactamente una cruz: HHHT, HHTH, HTHH, y THHH. ¿Cuál es la probabilidad de que Carrie saque exactamente una cruz?     A)   B)   C)   D)   Mostrar/Ocultar la Respuesta A) Incorrecto. Como hay dos resultados para cada moneda, existen 16 resultados posibles (2 • 2 • 2 • 2 = 16). Sin embargo, hay 4 resultados en el evento, entonces la probabilidad es  o .   B) Incorrecto. Como hay dos resultados para cada moneda, existen 16 resultados posibles (2 • 2 • 2 • 2 = 16). Hay 4 resultados en el evento, entonces la probabilidad es  o .   C) Correcto. Como hay dos resultados para cada moneda, existen 16 resultados posibles (2 • 2 • 2 • 2 = 16). Sin embargo, hay 4 resultados en el evento, entonces la probabilidad es  o .   D) Incorrecto. Hay dos resultados para cada moneda, pero hay 4 monedas. Esto significa que hay 16 posibles resultados (2 • 2 • 2 • 2 = 16). Existen 4 resultados en el evento, por lo que la probabilidad es  o .

 

 

 

La probabilidad nos ayuda a entender situaciones aleatorias o impredecibles donde varios resultados son posibles. Es una medida de qué tan probable es un evento, y depende de la razón entre los eventos y los posibles resultados, si todos los resultados son igualmente probables;

 

 

El Principio Fundamental de Conteo es un atajo para encontrar el tamaño del espacio muestral cuando hay demasiados experimentos y resultados:  

 

Cuando un experimento consiste en más de un elemento aleatorio, el número de resultados en el espacio muestral es igual al producto del número de resultados de cada elemento aleatorio.