
Deductive Reasoning
Deductive reasoningA form of logical thinking that uses generalizations to draw specific conclusions based on a series of logical steps, deductive reasoning may use rules, laws, and theories to support or justify a conjecture. is probably the most used process in all of mathematics. Anyone who has solved a logic puzzle like a Sudoku puzzle has used deductive reasoning. When we reason deductively, we use known facts to make logical conclusionsThe part of a logical statement that provides the result or consequences of the hypothesis—In a statement “If `x` then `y`,” the conclusion is `y`. that we know must be true. (We deduce one fact by putting together other facts.) This is different from inductive reasoningA form of logical thinking that makes general conclusions based on specific situations, inductive reasoning takes the path of observation to generalization to conjecture., which generalizesThe process of using observations of specific events to make statements or conjectures about more general situations. and makes conjectureA statement that attempts to make a conclusion but has not been proved true or false. based on observations rather than logic. Mathematicians (and all the rest of us, too) often use both inductive reasoning and deductive reasoning together.
Imagine we have recorded the results of experiments or observations, and decide that we see a pattern in the data. Or, imagine we have a problem to solve but aren't sure where to start, so we try to plug in some possible solutions to see what kinds of results we get. In these cases, we are reasoning inductively, making generalizations based on a limited number of observations. The trouble is, our generalizations might not be correct. Even with a lot of examples, it can be difficult if not impossible to be sure that there isn't at least one counterexampleA situation that provides evidence that a logical statement is false. we just haven't found yet.
For that reason, mathematicians, scientists, researchers, and other people who make conjectures will often follow up inductive reasoning with some deductive reasoning. They try to justifyProvide a logical argument for a conclusion or conjecture. the conjectures they made based on their observations. That is, they try to provide a logical argumentA series of statements, each verifiable as true, that lead to a conclusion., a series of verifiable statements that explains why their conjecture is always true.
Deductive reasoning is helpful when inductive reasoning is not appropriate, or there aren't enough examples to generalize from.
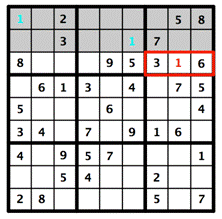
Consider puzzles like Sudoku. In a Sudoku puzzle, each row, column, and `3`-by-`3` box must be filled with the digits from `1` to `9`. A digit can't be used more than once in any single row, column, or box.

Inductive reasoning is no help in figuring out this puzzle. We could look at the solutions for other puzzles, and see where the digits were placed in each one. But if we generalize this to mean that we should fill the numbers in the same way every time, we won't be able to solve many puzzles!
What we can do instead is figure out the specific placements for this puzzle based on the rules of the game and the numbers that are given. In the top row of `3`-by-`3` boxes in the puzzle above, the left and middle boxes already have a `1`. The `1` in the right box can't be in the first or second rows, because they already have `1`'s. So the `1` for the right box has to be in the third row, and there's only one place for that. Deductive reasoning has revealed the location of the `1` in the right box!
Even without Sudoku, we've all used deductive reasoning a lot. Every time we work with an equation or mathematical expression to arrive at a conclusion or answer, we are using deductive reasoning—following the general principles of mathematics to find a specific solution that must be true.
|
Example |
|
|
Problem |
Terry does the following to factor the expression `3x^3 + 6x^2 + 3x`.
Is this inductive or deductive reasoning? |
|
|
Terry used the distributive property and other known facts to create a series of new facts about the expression `3x^3 + 6x^2 + 3x`. This is deductive reasoning. |
|
Answer |
Deductive reasoning |
|
Lucretia remembered this rule from arithmetic: To tell if fractions `a/b` and `c/d` are equal, “cross multiply” to find `ad` and `bc`.
She thought about whether this always works, and she made the following argument:
`(ad)/(bd)=(bc)/(bd)` `a/b*d/d=b/b*c/d` `a/b=c/d`
What kind of reasoning is Lucretia using?
A) Inductive reasoning
B) Deductive reasoning
|
The end result of deductive reasoning is often a logical argument. Most of the arguments we come across are polished, final arguments. We don't usually see the rough drafts, the mistakes, the lines of reasoning that went nowhere. We don't see that a writer started in a completely different place than the finished argument starts, and we can't tell when someone worked his argument out backwards because it was easier to figure it out from the conclusion than from the hypothesisThe part of a logical statement that provides the premise on which the conclusion is based—In a statement “If `x` then `y`,” the hypothesis is `x`.!
The point? Don't worry when it's hard to find a good argument right away. Deductive reasoning often takes some creativity and persistence. Time and practice will make it easier to sort out the dead ends from the promising leads.
The example below provides one way to approach building an argument:
|
Example |
||
|
Problem |
Frank has three siblings, and they all like to chip in to buy lottery tickets. Whenever there's a big jackpot, he wonders if it could be evenly divided among the four of them, just in case they win.
Frank has noticed that when a number formed by the last two digits of a whole number is divisible by `4`, the whole number itself is divisible by `4`. For example, `293,212` is divisible by `4` and `12` is divisible by `4`.
How can he use deductive reasoning to justify the truth of this divisibility test? |
|
|
Answer First, let's write a general example of the conjecture. That is, this example has to represent many examples, not just one.
In this case, we want to talk about the last two digits of a whole number. Here’s a trick that can be helpful when working with digits: Use place values to write the number as a sum with addends that are products of powers of `10`.
Since Frank is interested in the last two digits of a larger number, we can separate those digits from the rest of the number. For example, `236` can be written as `200 + 36`, or `2(100) + 36`. The number `72,915` can be written as `72,900 + 15`, or `729(100) + 15`. |
||
|
Any whole number can be written as `100a + b`, where `a` and `b` are whole numbers and `b<100`. |
To put it in general terms, a large number can be written as `100` times a number plus a second number that is less than `100`. This is a general, known statement. |
|
|
If `b` is divisible by `4`, then `100a + b` is divisible by `4`. |
We can also write Frank's conjecture using algebraic expressions. |
|
|
|
Now we need to find a way to connect the general example to the conclusion. This may take several steps. |
|
|
`100a+b=4(25a+b/4)` |
In this case, we want `100a + b` to be divisible by `4`. So let’s factor the `4` out of the expression. |
|
|
|
What does it mean for the number to be divisible by `4`? It means the quotient is a whole number, so we want `25a+b/4` to be a whole number. How can we show that it is? |
|
|
Since `a` is a whole number, `25a` is also a whole number. |
We can use the hypothesis here. We defined `a` to be a whole number, so `25a` has to also be a whole number. |
|
|
Since `b` is divisible by `4`, `b/4` is a whole number. That means `25a+b/4` is a whole number. |
The hypothesis is that `b` is divisible by `4`, so that gives us information about `b/4`. Combine that with the information about `25a`. |
|
|
Since `100a+b=4(25a+b/4)`, we know that `(100a+b)/4=25a+b/4`. Since `25a+b/4` is a whole number, `100a + b` is divisible by `4`. |
Conclude the argument. |
|
Here are some tips for building an argument. None of them will work every time, and we may need to try them all before we find an argument that works.
|
|
|
Build a logical argument to explain why a two-digit number is divisible by `3` if the sum of its digits are divisible by `3`.
Hint: Write the two-digit number as `10x + y`, and notice that `10x = 9x + x`.
|
Deductive reasoning is a process of making conclusions by putting known facts together to provide a reasoned argument for a new fact. Deductive reasoning can be used to justify a conjecture arrived at through inductive reasoning. It's also helpful at times when inductive reasoning isn't appropriate, such as when there aren't enough examples to generalize from.