Understanding Logical Statements
Learning Objectives
- Identify the hypothesis and conclusion in a logical statement.
- Determine whether mathematical statements involving linear, quadratic, absolute value expressions, equations, or inequalities are always, sometimes, or never true.
- Use counterexamples to show that a statement is false, and recognize that a single counterexample is sufficient.
Introduction
Logic is an essential part of the study of mathematics. Much of mathematics is concerned with the characteristics of numbers and other mathematical objects (such as geometric figures or variables), and being able to make decisions about what must be true based on known characteristics and other facts is vital.
The Parts of a Logical Statement
A logical statementA statement that allows drawing a conclusion or result based on a hypothesis or premise. is a statement that, when true, allows us to take a known set of facts and infer (or assume) a new fact from them. Logical statements have two parts: The hypothesisThe part of a logical statement that provides the premise on which the conclusion is based. In a statement “If `x` then `y`,” the hypothesis is `x`., which is the premise or set of facts that we start with, and the conclusionThe part of a logical statement that provides the result or consequences of the hypothesis. In a statement “If `x` then `y`,” the conclusion is `y`., which is the new fact that we can infer when the hypothesis is true. (Note: If you've used hypothesis in science class, you've probably noticed that this is a fairly different definition. Be careful not to get confused!)
Consider this statement:
If you go outside without any rain gear or cover when it’s pouring rain, you will get wet.
Here, the hypothesis is “you go outside without any rain gear or cover when it’s pouring rain.” The hypothesis must be completely true before we can use the statement to infer anything new from it. What does this statement say about someone who doesn’t go outside? About someone who uses an umbrella? About what happens to someone when it’s not pouring rain? Nothing. This statement doesn't apply to anyone in those cases.
The conclusion of this statement is “you will get wet.” Suppose it’s raining, and someone walks outside, and doesn't have any rain gear or other kind of cover—what will happen? All the parts of the hypothesis have been met, so—if the statement is true—we can infer that the person is going to get wet. It certainly seems reasonable that they would!
Note that in this example, if the hypothesis isn’t true, the person still could get wet. On a sunny day with no rain, someone might go outside to wash his car and get sprayed by the hose. Someone else might go swimming, and then they would really get wet! The statement says nothing when the hypothesis is false. It's only helpful when the hypothesis is true.
Not all logical statements are written as “If (something is true) then (something else is true).” To identify the hypothesis and conclusion, you may need to try to rewrite a statement in an “if-then” format.
|
Example
|
|
Problem
|
Identify the hypothesis and conclusion in the statement, “I get a headache every time I sleep for more than nine hours.”
|
|
|
If I sleep for more than nine hours, then I get a headache.
|
|
This statement isn’t written as an “if-then” statement, so rewrite it in those terms. Be sure the new statement says essentially the same thing as the original!
|
|
Answer
|
Hypothesis: I sleep for more than nine hours
|
|
The hypothesis is the “if” portion of the statement.
|
|
|
Conclusion: I get a headache
|
|
The conclusion is the “then” portion of the statement.
|
Logical statements can also be about mathematics, of course! Anything that lets us infer a new fact about something mathematical from given information is a logical statement. For example, “The diagonals of a rectangle have the same length” is a logical statement. The hypothesis is the part that can help us if we know it’s true. When could this statement be useful?
|
Example
|
|
Problem
|
Identify the hypothesis and conclusion in the statement, “The diagonals of a rectangle have the same length.”
|
|
|
If a figure is a rectangle, then its diagonals have the same length.
|
|
Rewrite in “if-then” form.
In this statement, the figure being a rectangle is the given information, and the equality of the diagonals is the new fact inferred from the known fact.
|
|
Answer
|
Hypothesis: a figure is a rectangle
|
|
|
|
|
Conclusion: the diagonals have equal length
|
|
|
With algebraic statements, the hypothesis is often an assumption about what values are allowed for a variable. For example, you might have seen a statement like “`a + b = b + a`, where `a` and `b` are real numbers.” Let's treat this equation as a logical statement:
|
Example
|
|
Problem
|
Identify the hypothesis and conclusion in the statement, “`a + b = b + a`, where `a` and `b` are real numbers.”
|
|
|
If `a` and `b` are real numbers, then `a + b = b + a`.
|
|
Rewrite as an “if-then” statement.
|
|
Answer
|
Hypothesis: `a` and `b` are real numbers
|
|
The hypothesis is the “if” part of the statement.
|
|
|
Conclusion: `a + b = b + a`
|
|
The conclusion is the “then” part of the statement.
|
|
Consider this statement:
`|x| >=0` for all real numbers `x`.
Which of the following provides the best identification of the hypothesis and conclusion for this statement?
A) The hypothesis is “`|x| >=0`” and the conclusion is “all real numbers `x`.”
B) The hypothesis is “`x` is a real number” and the conclusion is “`|x| >=0`.”
C) The hypothesis is “all real numbers `x`” and the conclusion is “`|x| >=0`.”
D) The hypothesis is “`|x| >=0`” and the conclusion is “for all real numbers.”
A) Incorrect. “All real numbers `x`” is a phrase that doesn't have any meaning, so it can't be the conclusion. A way to rewrite this as an “if-then” statement would be, “If `x` is a real number, then ` |x| >=0`.” The hypothesis is “`x` is a real number” and the conclusion is “` |x| >=0`.”
B) Correct. A way to rewrite this as an “if-then” statement would be, “If `x` is a real number, then ` |x| >=0`.” The hypothesis is “`x` is a real number” and the conclusion is “` |x| >=0`.”
C) Incorrect. “All real numbers `x`” isn’t a fact that we can use to make a conclusion. A way to rewrite this as an “if-then” statement would be, “If `x` is a real number, then ` |x| >=0`.” The hypothesis is “`x` is a real number” and the conclusion is “` |x| >=0`.”
D) Incorrect. “For all real numbers” is incomplete. Unless `x` is specified, there isn't any connection between the hypothesis and conclusion. A way to rewrite the statement as an “if-then” statement would be, “If `x` is a real number, then ` |x| >=0`.” The hypothesis is “`x` is a real number” and the conclusion is “` |x| >=0`.”
|
Critical thinking is important, not just in mathematics but in everyday life. Have you ever heard someone make a statement and then thought, “Wait. Is that true?” Sometimes people have reasons for thinking something is true even though it isn’t. Determining if a statement is true is a great skill to have!
When determining if a statement is true, most people start by looking for examplesA situation that suggests a logical statement may be true., which are situations for which the statement does turn out to be true (both the hypothesis and the conclusion are true). A more powerful situation to find, if one exists, is a counterexampleA situation that provides evidence that a logical statement is false., a situation for which the statement turns out to be false (the hypothesis is true, but the conclusion is false). Why are counterexamples so powerful?
Consider a person who sees the moon many times at night and then thinks: I’ve never seen the moon during the day. The person might then make the statement, “The moon only comes out at night.” As an if-then statement, this is the same as “If the moon is out, then it’s night.” We can all probably think of many times when we saw the moon out, and it was nighttime. These are examples, situations when the statement was true.
But in fact, the statement is not always true, and we only need to see the moon during the day once—only one counterexample—to know that the statement is not true. Many, many examples cannot prove the statement is true, but we only need one counterexample to prove it’s not!
For a given statement, then, we have three possibilities:
| The truthfulness of logical statements |
| A statement is: |
if: |
| Always true |
There are examples but no counterexamples |
|
Sometimes true
|
There is at least one example and at least one counterexample |
| Never true |
There are no examples, only counterexamples |
So how can we be sure if something is true (or never true for that matter), if we can’t rely on lots of examples? With algebraic statements, sometimes we can turn to a graph for help:
|
Example
|
|
Problem
|
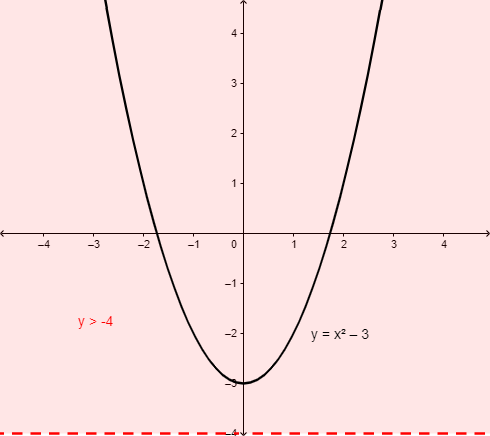
Is the following statement always, sometimes, or never true?
`x^2-3> -4`, for all real numbers `x`
|
|
|

|
Graph the function `y = x^2-3`.
|
|
|
|
Note where `y> -4`.
The entire graph is in the region where `y> -4`, so the statement is always true.
|
|
Answer
|
always true
|
|
|
Another way to decide if something is always, sometimes, or never true is reasoning from other things we know are true. We can start with something we know is true and try to create the original statement. Let’s try this with the same example above:
|
Example
|
|
Problem
|
Is the following statement always, sometimes, or never true?
`x^2-3> -4`, for all real numbers `x`
|
|
|
`x^2>=0`, for all real numbers `x`
|
|
The conclusion is an inequality involving `x^2`. We know that `x^2` is always positive or `0` for all real numbers `x`.
Now we'll use algebra to make this true statement look more like the original statement. This may require more than one step.
|
|
|
`x^2-3>=-3`, for all real numbers `x`
|
|
First, subtract `3` from both sides.
|
|
|
`x^2-3>=-3> -4`, for all real numbers `x`
|
|
Then note that `-3> -4`.
|
|
|
`x^2-3> -4`, for all real numbers `x`
|
|
This means the original statement is always true!
|
|
Answer
|
always true
|
|
|
When we try to put together logical arguments like that, the biggest problem can be knowing where to start. There's a good chance our first attempt(s) will run into a dead end, and we'll need to start over. Practice does make it easier. Sometimes it helps to work backward: start by assuming the conclusion is true, try to think of a related statement known to be true (or false), and then connect them. Let’s take one last look at the example above:
|
Example
|
|
Problem
|
Is the following statement always, sometimes, or never true?
`x^2-3> -4`, for all real numbers `x`
|
|
|
If `x^2-3> -4`, for all real numbers `x`…
|
|
If you don’t know where to start, assume the conclusion is true.
|
|
|
Then `x^2> -1`, for all real numbers `x`
|
|
Now look for something that you know is true. Often this means simplifying expressions or solving equations.
In this case, add `3` to both sides to get `x^2` by itself.
|
|
|
Not only is `x^2> -1, x^2>=0`, which is even better (because `0> -1`).
|
|
When you find something that you know is true (or false), you’ve found your starting point!
|
|
|
`x^2>0`, for all real numbers `x`.
That means `x^2> -1`, for all real numbers `x`.
So `x^2 - 3> -4`, for all real numbers `x`.
|
|
Now that you have a starting point, you can work backwards to explain how you know the statement is always true.
|
|
Answer
|
always true
|
|
|
Another way to test the truth of a statement is to look for counterexamples. Graphs can help us there, too:
|
Example
|
|
Problem
|
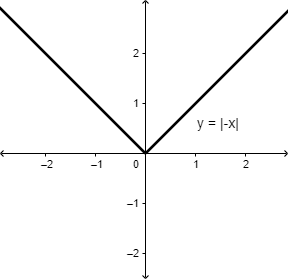
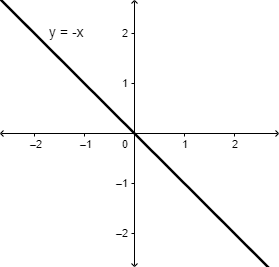
Is the following statement always, sometimes, or never true?
`|-x| = -x`, for all real numbers `x`
|
|
|
|
|
Graph both sides of the equation: `y=|-x|`
and `y = -x`
|
|
|

Examples (statement true):
`x = 0, x = -3`
Counterexamples (statement false):
`x = 1, x=100`
|
|
Since the statement suggests these two graphs should be identical, examples come from where they match.
Counterexamples come from where they don’t coincide.
For this statement, there is at least one example and at least one counterexample.
|
|
Answer
|
Sometimes true
|
|
|
Although we know `|-x| = -x` is not always true if `x` is any real number, we also know that it is sometimes true. In fact, we can specify when it’s true—using the graph from the example, we can see it’s true when `x<=0`. We can use that fact to create a new statement:
If `x<=0`, then `|-x| = -x`.
Because of the narrower hypothesis, this statement is always true.
|
Is the following statement always, sometimes, or never true?
`-2x^2 + 8x + 10>18`, for all real numbers `x`
A) Always
B) Sometimes
C) Never
The correct answer is never true. The graph opens down because the coefficient on `x^2` is negative, so you can find the maximum value by graphing or completing the square to find the vertex of `-2x^2 + 8x + 10`, which is `(2, 18)`. The graph never gets above `18`, so the statement is never true.
|
Special Cases
When we look for examples, and particularly for counterexamples, there are some special cases that are easy to overlook. Keeping these cases in mind is often very helpful. Look through some special cases and consider if any of them provides a counterexample for this statement: “When two numbers are multiplied, the product is larger than each of the factors.”
|
Special cases for examples and counterexamples
Keep an eye out for these cases when determining whether a mathematical statement is always, sometimes, or never true.
|
|
Zero
|
Zero can be an issue in the following types of expressions:
- Rational expressions (because the denominator cannot be `0`)
- Expressions involving exponents (if the base is `0`, the exponent cannot be negative or `0`, and with positive exponents the expression evaluates to `0`; if the base is not `0` but the exponent is, the expression evaluates to `1`)
- Expressions involving even roots (there is only one root instead of two)
- Expressions involving absolute values (the only time absolute value is not positive is when the expression inside the absolute value sign is `0`)
|
|
Negative numbers
|
These can be an issue in the following types of expressions:
- Expressions involving even roots (a negative number has no real number roots)
- Expressions involving exponents (if the exponent is negative, the base cannot be `0`; if the exponent is a fraction with an even denominator—indicating an even root—the base cannot be negative; if the base is negative and the exponent varies, the expression’s value can switch between negative for odd exponents and positive for even exponents)
- Expressions involving absolute values (if `x` is positive or `0`, then `|x| = x`, but if `x` is negative, then `|x| = -x`, that is, the absolute value is the opposite of `x`)
|
|
Fractions
|
Fractions can be issues in the following cases:
- When only whole number answers make sense, such as in questions about undividable objects (for example, people or vehicles)
- Expressions involving exponents (since fractional exponents can be interpreted as roots, negative bases can become an issue)
|
|
Fractions between
`0` and `1`
|
Although fractions are mentioned above, these are important in different ways.
- When multiplying, the product of two numbers larger than `1` will always be larger than either number. However, if at least one of those numbers is between `0` and `1`, this is not the case. (For example, `0.5*6=3`, which is greater than `0.5` but less than `6`.)
- Expressions involving exponents have a similar issue. A base greater than `1` will give a result larger than the base when taken to a power greater than `1`. However, if the base is between `0` and `1`, or the exponent is between `0` and `1`, the result is closer to `0` than the original base.
|
Here are some more examples. Consider the special cases above as you read through these.
|
Example
|
|
Problem
|
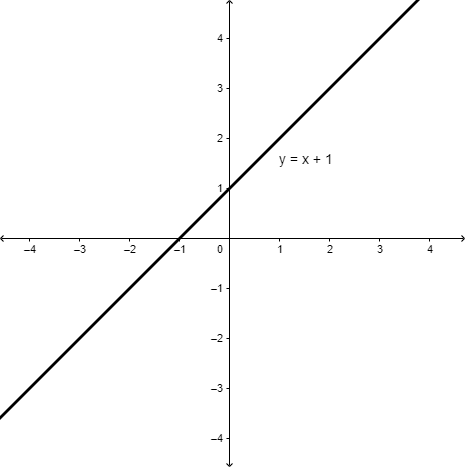
Is the following statement always, sometimes, or never true?
`(x^2-1)/(x-1)=x+1`, for all real numbers `x`
|
|
|
`(x^2-1)/(x-1)=((x+1)(x-1))/(x-1)`
|
|
The left side is a rational expression that can be simplified. Start by factoring the numerator.
|
|
|
`((x+1)(x-1))/(x-1)=((x-1)/(x-1))(x+1)=x+1`
|
|
The numerator and denominator both have a common factor of `(x - 1)`, so we can simplify the rational expression.
|
|
|
|
|
The simplified expression is the same as the right side of the original statement, and a graph (made with a graphing calculator or computer) will show the same line as `y = x + 1`. So we might think the statement is always true.
|
|
|
`(x^2-1)/(x-1)=x+1`
`((1)^2-1)/(1-1)=1+1`
`0/0=2`
|
|
But let’s look at our special cases. When we have a rational expression, a value of `0` is important to think about. In this case, the problem isn’t when `x` is `0` but when the denominator, `x - 1`, is `0`. Try putting `x = 1` into the statement.
|
|
Answer
|
Sometimes true (true when `x!=1`)
|
|
There is one counterexample that makes the statement sometimes true: `x=1`.
|
|
Example
|
|
Problem
|
Is the following statement always, sometimes, or never true?
`x^2<x`, for nonnegative (positive or `0`) real numbers `x`
|
|
|
If `x = 0`, `x^2 = 0`, so `x^2 = x`.
If `x = 1`, `x^2 = 1`, so `x^2 = x`.
If `x = 2`, `x^2 = 4`, so `x^2>x`.
If `x = 10`, `x^2 = 100`, so `x^2>x`.
|
|
Try a few examples. For these examples, the statement is false!
|
|
|

|
|
Let’s take a look at the graphs. Graph both sides of the equation: `y = x^2` and `y=x`.
|
|
|

|
|
The statement says `x^2<x`, so look to see if there’s anywhere that the graph of `y = x^2` is below the graph of `y=x`.
When `x` is between `0` and `1`, the graph of `x^2` is below the graph of `x`.
|
|
Answer
|
Sometimes true
(true when `0<x<1`)
|
|
|
|
Is the following statement always, sometimes, or never true?
`2|x + 3| = 2x + 6`, for all real numbers `x`
A) Always
B) Sometimes
C) Never
The correct answer is sometimes true. When `x + 3` is `0` or greater, ` |x + 3| = x + 3`, so for `x>=-3`, this is true. However, when `x + 3` is less than `0`, ` |x + 3| = -(x + 3)`, so for `x<-3`, `2|x + 3| = -2x - 6`, the opposite of `2x + 6`. The statement is sometimes true.
|
Summary
Logical statements have two parts, a hypothesis that presents facts that the statement needs to be true, and a conclusion that presents a new fact we can infer when the hypothesis is true.
For a statement to be always true, there must be no counterexamples for which the hypothesis is true and the conclusion is false. If there are examples for which the statement is true, but there are also counterexamples, then the statement is sometimes true. These sometimes true statements can be made into always true statements by changing the hypothesis. A statement is never true if there are no examples for which both the hypothesis and the conclusion are true. When looking for counterexamples and examples, there are some special cases (such as negative numbers and fractions) that should be considered.







