
Number Sets
Mathematicians recognize several sets of numbers that share certain characteristics. These categories are helpful to know when only certain kinds of numbers are valid for values and variables. Our understanding and classification of the different sets of numbers has developed over thousands of years.
Early civilizations found different ways to write numbers, but they all started with the same set of numbers preschool children learn today: the natural numbersAlso called counting numbers, the numbers `1, 2, 3, 4`, ... (also called the counting numbersAlso called natural numbers, the numbers `1, 2, 3, 4`, ...). These are the numbers `1`, `2`, `3`, and so on—the numbers we use when counting. They are natural because our natural understanding of numbers begins with noticing multiple copies of things, like how many fingers we have, or the size of sets, like how many toys we have.
Although the earliest civilizations understood “nothing”—they knew when they had no cows, or no children, of course—the number zero has an interesting history. The first use of a symbol to represent “nothing” wasn't until `300` BC. The Babylonian number system used the symbols only as a placeholder in a place value system, much as we use `0` in the number `702` to represent no `10`'s. The earliest recognition of zero as a number, in the same way that `1` and `23` are numbers, is uncertain, but may date to the `9`th century in India. When `0` is added to the set of `1`, `2`, `3`, and so on, it forms the whole numbersThe numbers `0`, `1`, `2`, `3`,..., or all natural numbers plus `0`. . These are called “whole” because they have no fractional parts.
The integersThe numbers ...,`−3,−2,−1,0,1,2,3`,... are the whole numbers plus their negative counterparts: ..., `-3, -2, -1, 0, 1, 2, 3`,... Negative numbers first appeared in China as early as the first century BC. (That’s as much as `1000` years before zero was recognized as a number itself!) However, despite their usefulness in representing concepts such as debt, it has only been since the `18`th century—less than `300` years ago—that they gained widespread acceptance as actual numbers.
|
Which of the following sets does the number `0` belong to?
natural numbers whole numbers integers
A) Natural numbers only
B) Whole numbers only
C) Natural and whole numbers
D) Integers only
E) Whole numbers and integers
|
Fractional numbers have been around for much longer than zero or negative numbers. Ancient Egyptians (from as early as the `21`st century BC) studied fractions. Today, fractional numbers are included in the set of rational numbersNumbers that can be written as a ratio of integers (that is, as `p/q` where `p` and `q` are both integers and `q ≠ 0`)., which are numbers that can be written in the form `p/q` where `p` and `q` are both integers. Rational numbers can be written in many forms. For example, `17/3` can also be written as `5 2/3`, `5.66`…, or `5.bar6`. Regardless of the form used, because this number can be written as the ratio of two integers, the number is rational.
Note that all integers (and that means all whole numbers and natural numbers) are rational numbers because they can be written using `1` as the denominator `q`. For example, `-3` can be written as `(-3)/1`, so it is rational as well.
So far, the types of numbers we have described create a nesting series of sets. We began with the natural numbers, then expanded that set with `0` to form the whole numbers. Then we included negative numbers with the whole numbers to create the integers. Now we have the rational numbers, which includes all the integers plus many other numbers. This diagram shows how these number sets are “nested”:

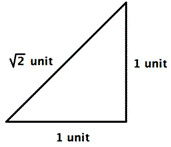
The Greek mathematician Pythagoras, for whom the Pythagorean Theorem is named, was the leader of a group known as the Pythagoreans. They believed that all quantities could be expressed as a natural number or a ratio of natural numbers. Legend tells that they believed this so fervently that when one of their members used the Pythagorean Theorem to prove that the hypotenuse of the triangle below cannot be expressed as a ratio of natural numbers, they exiled him. (Or worse—some stories say they threw him overboard while at sea and watched him drown!)
Today we know that the Pythagoreans' thinking was wrong, and there are indeed quantities that are not rational. These irrational numbersNumbers between integers that cannot be written as a ratio of integers (that is, as `p/q` where `p` and `q` are both integers), the decimal representation of an irrational number is non-repeating and non-terminating. cannot be expressed as a ratio of integers. Any square root of a number that is not a perfect square, for example `sqrt2`, is irrational.
Irrational numbers are most commonly written in one of three ways: as a root, using a special symbol (such as `pi`), or as a nonrepeating, nonterminating decimal.
Numbers with a decimal part can either be terminating or nonterminating. Terminating means the digits stop eventually (although we can always write `0`'s at the end). A nonterminating decimal has digits (other than `0`) that continue forever. For example, consider the decimal form of `1/3`, which is `0.3333`…. The `3`'s continue indefinitely. Or the decimal form of `1/11`, which is `0.090909`…: the sequence “`09`” continues forever.
In addition to being nonterminating, these two numbers are also repeating decimalsNumbers whose decimal parts repeat a pattern of one or more digits, these are all rational numbers.. Their decimal parts are made of a number or sequence of numbers that repeats again and again. A decimal is nonrepeating if the digits never form a repeating pattern. The value of `sqrt2`, for example, is `1.414213562`…. No matter how far we carry out the numbers, the digits will never repeat a previous sequence.
If a number is terminating or repeating, it must be rational; if it is both nonterminating and nonrepeating, the number is irrational.
Consider a terminating decimal, like `3.529`. Since this number has a terminating decimal, it is a rational number. We can write `3.529` as a ratio of integers: the numerator is the number without the decimal point (in this case, `3,529`) and the denominator is a power of `10` corresponding to the place value of the last digit. Since the `9` is in the thousandths place, the denominator is `1,000`. (Another way to do this is to count the decimal places to the right of the decimal point in the original number. The denominator is `1` followed by that many `0`'s. There are three digits to the right of the decimal place in `3.529`, so the denominator is `1` followed by three `0`'s.)
`3.529=(3,529)/(1,000)`
Here's one more example:
|
Example |
|||
|
Problem |
Write `-82.91` as a ratio of integers. |
||
|
|
numerator: `-8291` |
|
The numerator is the number without a decimal point. |
|
|
denominator: `100` |
|
There are `2` decimals to the right of the decimal point, so the denominator is `1` with two `0`'s (that is, `100`). |
|
Answer |
`(-8291)/(100)` |
|
|
What about a nonterminating, repeating decimal? Here’s one method for expressing a repeating decimal as a ratio of integers. It works with all repeating decimals:
`1`. Write an equation, `x =` the number with a bar over the repeating portion.
`2`. Count how many digits are in the repeating portion of the decimal, and multiply both sides of the equation in step `1` by `10` raised to that power to create a second equation. (For example, if there are `3` digits that repeat, multiply by `10^3` or `1000`.) Keep the repeating portion the same, even if you could move the repetition bar over.
`3`. Subtract the equation in step `1` from the equation in step `2`. In doing this, the repeating decimal parts will line up. All the digits from that point on will be `0`'s.
`4`. Divide both sides of the new equation in step `3` by the coefficient of `x`.
`5`. Multiply both numerator and denominator by `10` until any decimals are removed, or rewrite the number in lowest terms.
Let’s try it to see if it makes sense:
|
Example |
||||||||||||||
|
Problem |
Write `8.9282828`… as a ratio of integers. |
|||||||||||||
|
|
`x=8.9bar(28)`
|
Write an equation setting `x` equal to the number with a bar over its repeating portion. |
||||||||||||
|
|
`100x=892.8bar(28)`
|
The repeating part has two digits, so multiply by `10^2` or `100`. Redraw the bar over the repeating digits at the end. |
||||||||||||
|
|
|
Subtract the equations to remove the repeating portions of the decimals. |
||||||||||||
|
|
`x=(883.9)/(99)` |
To solve for `x`, divide by the coefficient of `x`. |
||||||||||||
|
|
`(883.9)/(99)(10/10)=8839/990`
|
Multiply both numerator and denominator by `10` to express the number as a ratio of integers. |
||||||||||||
|
Answer |
`8839/990` |
|
|
|||||||||||
That did work! We were able to write a nonterminating but repeating decimal as the ratio of two integers. That proves that the number is rational.
|
Is `-382.9bar(892)` rational or irrational?
A) Rational B) Irrational
|
The set of real numbersThe set of numbers that includes both rational numbers and irrational numbers. is made by combining the set of rational numbers and the set of irrational numbers. The set of real numbers is all the numbers that have a location on the number line.
|
Sets of numbers
Natural numbers: `1, 2, 3`,...
Whole numbers: `0, 1, 2, 3`,...
Integers: ..., `-3, -2, -1, 0, 1, 2, 3`,...
Rational numbers: any number that can be expressed in the form `p/q`, where `p` and `q` are integers, rational numbers are terminating or repeating when written in decimal form
Irrational numbers: any number that cannot be written as `p/q` (where `p` and `q` are integers), irrational numbers are nonterminating and nonrepeating when written in decimal form
Real numbers: any number that is rational or irrational
|
The diagram below shows how all the real numbers are related to each other. Notice there is no overlap between the rational numbers and the irrational numbers, and the two sets together make up the set of real numbers.
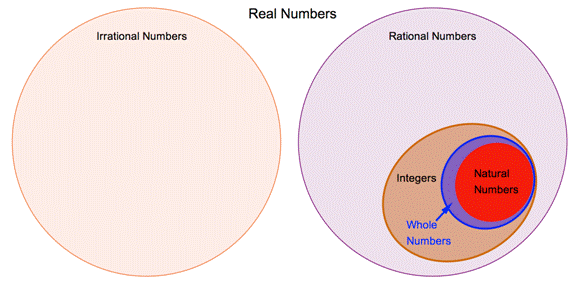
The numbers that can be represented on a number line are called real numbers. These numbers can be separated into two sets that have no numbers in common: the irrational numbers and the rational numbers. Irrational numbers have decimal forms that are nonterminating and nonrepeating. Rational numbers have decimal forms that are terminating or repeating. Inside the set of rational numbers are several smaller, nested sets: integers, whole numbers, and natural numbers.
The sets of numbers are defined as follows:
|
Real numbers |
any number that is rational or irrational |
|
Rational numbers |
any number that can be written as the ratio of two integers and that is terminating or repeating in decimal form |
|
Integers |
..., `-3, -2, -1, 0, 1, 2, 3`,... |
|
Whole numbers |
`0, 1, 2, 3`,... |
|
Natural numbers |
`1, 2, 3`,... |
|
Irrational numbers |
any number that can't be written as the ratio of two integers and that is nonterminating and nonrepeating in decimal form |