Solving Quadratic Equations by Completing the Square
Sometimes a quadratic equationAn equation that can be written in the form `ax^2+bx+c=0` where `a!=0`. When written as `y = ax^2 + bx + c`, the expression becomes a quadratic function. is impossible to factor. To solve this kind of quadratic equation, different strategies are needed. Completing the squareThe process of changing a polynomial of the form `x^2+bx` into a perfect square trinomial , or `x^2+bx+(b/2)^2`, or `(x+b/2)^2`. is such a strategy. It turns a polynomial into a perfect square trinomialA three-term polynomial., which is easier to graph and to solve.
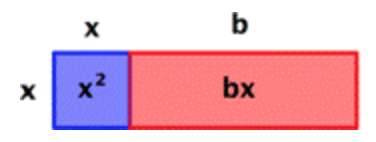
“Completing the Square” does exactly what it says—it takes something that probably is not a square and makes it one. We can illustrate this idea using an area model of the binomial `x^2 + bx`:
 |
`x(x+b)=x^2+bx` |
In this example, the area of the overall rectangle is given by `x(x + b)`.
Now let's make this rectangle into a square. First, we'll divide the red rectangle with area `bx` into two equal rectangles each with area `b/2x`. Then we'll rotate and reposition one of them. We haven't changed the size of the red area—it still adds up to `bx`.
 |
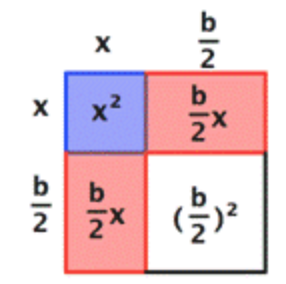 |
`x^2+2(b/2)x+(b/2)^2` |
The red rectangles now make up two sides of a square, shown in white. The area of that square is the length of the red rectangles squared, or `(b/2)^2`.
Here comes the cool part—do you see that when the white square is added to the blue and red regions, the whole shape is now a square, too? In other words, we've “completed the square!” By adding the quantity `(b/2)^2` to the original binomial, we've made a square, a square with sides of `x+b/2`:
 |
`x^2+bx+(b/2)^2=x^2+2(b/2)x+(b/2)^2=(x+b/2)^2` |
Notice that the area of this square can be written in two ways, as `x^2+bx+(b/2)^2`, and as `(x+b/2)^2`.
|
Completing the Square
To complete the square on an expression of the form `x^2 + bx`, add `(b/2)^2`. Then the expression becomes `x^2+bx+(b/2)^2=(x+b/2)^2`.
|
Let’s look at an example using numbers instead of an area model. We'll complete the square for the binomial `x^2+8x`. To do that, we need to find a value `c` so `x^2+8x+c` becomes a perfect squareAny of the squares of the integers. Since `1^2 = 1`, `2^2 = 4`, `3^2 = 9`, etc., `1`, `4`, and `9` are perfect squares. trinomial.
|
Example |
|||
|
Problem |
Find `c` such that `x^2+8x+c` is a perfect square trinomial. |
||
|
|
`x^2+8x+(8/2)^2`
|
|
To complete the square, add `(b/2)^2`.
`b = 8`, so `(b/2)^2=(8/2)^2`. |
|
|
`x^2+8x+(4)^2`
`x^2+8x+16` |
|
Simplify.
|
|
Answer |
`c = 16` |
|
|
Our perfect square trinomial is `x^2+8x+(4)^2`. We can also write that as the square of a binomial: `(x+4)^2`.
Notice that `(b/2)^2` is always positive, since it is the square of a number. When we complete the square, we are always adding a positive value.
|
Use completing the square to find the value of `c` that makes `x^2-12x+c` a perfect square trinomial. Then write the expression as the square of a binomial.
A) `c = 12`; `(x-6)^2`
B) `c=36`; `(x+6)^2`
C) `c=-12`; `(x-12)^2`
D) `c=36`; `(x-6)^2`
|
When we solve a quadratic equation that has been set equal to zero, such as `3x^2+2x-7=0` or `x^2-10=0`, we find the value(s) of `x` that makes the equation true. When we start with a quadratic function, such as `y=ax^2+bx+c`, we find the roots of a quadratic equationThe `x`-intercepts of the parabola or the solution of the equation. by setting the `y` equal to zero and solving. This can be called “solving the quadratic.” The roots of `y=ax^2+bx+c` are located on the graph where the parabola crosses or touches the `x`-axis. They are also called the x-interceptsThe point where a line meets or crosses the `x`-axis. of the graph. For quadratic equations that can be factored, such as `y=x^2+3x+2` or `y=x^2-x-12`, we find the roots by setting the equation equal to zero and using the zero property to find any possible `x`-coordinates.
But how would we find the roots for a quadratic equation that cannot be factored? There are many non-factorable quadratic equations that still have solutions or roots. We can use completing the square to help us solve a quadratic equation that cannot be solved by factoring. Here is an example:
|
Example |
|||
|
Problem |
Find the roots of the quadratic equation `x^2-4x+1=y`. |
||
|
|
`x^2-4x+1=0`
|
The roots are the `x`-intercepts, where the graph crosses the `x`-axis. The `y` value for any point on the `x`-axis is `0`, so substitute `0` for `y`.
|
|
|
|
`x^2-4x=-1`
`x^2-4x+(b/2)^2=-1+(b/2)^2`
`x^2 - 4x + 4 = -1 + 4`
`x^2 - 4x + 4 = 3` |
Rewrite the equation with the left side in the form `x^2 + bx`, to prepare to complete the square.
Add `(b/2)^2` to the left side to complete the square, and also to the right side so the equation is still true. `b = -4`, so `(b/2)^2=((-4)/2)^2=4`. |
|
|
|
`(x-2)^2=3` |
Rewrite the left side as a binomial squared. |
|
|
|
`x-2=sqrt3` or `x-2=-sqrt3`
|
Take the square root of both sides. We need both the positive and negative square root, or we’ll miss one of the solutions. |
|
|
|
`x=2+sqrt3` or `x=2-sqrt3`
|
Solve for `x`. These are the `x`-coordinates of the roots. |
|
|
Answer |
`2+sqrt3` or `2-sqrt3` |
||
Remember that when we take square roots of both sides of an equation, the answer is both the positive and negative value of the square root. Mathematicians use a special symbol for this: `+-`, which is read as “plus or minus.” Using this symbol, the pair of equations above, `x-2=sqrt3` and `x-2=-sqrt3`, could be written as one equation: `x-2=+-sqrt3`.
The above example showed a quadratic equation that has a coefficient of `1` on the squared term. We can work the same way if the coefficient is a number other than `1`, but we must remember to divide both sides of the equation by this coefficient before completing the square.
|
Example |
|||
|
Problem |
Solve `2x^2+12x-16=0`. |
||
|
|
`x^2+6x-8=0`
|
|
Divide both sides of the equation by the coefficient of `x^2`, which is `2`. |
|
|
`x^2+6x=8`
|
|
Rewrite the equation so the left side has the form `x^2+bx`. |
|
|
`x^2+6x+(3)^2=8+9`
|
|
Add `(6/2)^2=(3)^2=9` to both sides to complete the square. |
|
|
`(x+3)^2=17` |
|
Write the left side as a binomial squared. |
|
|
`x+3=+-sqrt17`
|
|
Take square roots of both sides, noting both positive and negative possibilities. |
|
|
`x=-3+-sqrt17`
|
|
Solve for `x`. This gives the `x`-coordinates of the roots, or the solutions to the quadratic equation. |
|
Answer |
`-3+sqrt17` or `-3-sqrt17` |
||
In both of the problems we just solved, each quadratic equation had two solutions, which means the equation represents a parabola with two roots. Think for a moment about the case of one root or solution. In that case, the graph of the quadratic will touch the `x`-axis in one place and the solution will have only one `x`-coordinate value.
What about parabolas that never meet the `x`-axis? In those cases, we will find ourselves needing to take the square root of a negative number as we solve the equation. You cannot take the square root of a negative number, which is the tip-off that there is no root.
Quadratic equations can also have just one solution. Here is an example:
|
Example |
|||
|
Problem |
Solve `x^2+16x+64=0`. |
|
|
|
|
`x^2+16x=-64`
|
|
Rewrite the equation so the left side has the form `x^2+bx`. |
|
|
`x^2+16x+(8)^2=-64+64`
|
|
Add `(16/2)^2=(8)^2=64` to both sides. |
|
|
`(x+8)^2=0`
|
|
Write the left side as a binomial squared. |
|
|
`x+8=0`
|
|
Take the square root of both sides. Normally both positive and negative square roots are needed, but `0` is neither positive nor negative. `0` has only one root. |
|
|
`x=-8` |
|
Solve for `x`. This is the solution to the quadratic equation, and the `x`-coordinate of the root of the quadratic function `y=x^2+16x+64`. |
|
Answer |
`x=-8` |
|
|
We also could have solved the equation by noticing that the trinomial was already a perfect square and going straight to rewriting it as a binomial squared.
Completing the square is also a useful tool when converting a quadratic equation that is in the standard form of a quadratic equationWritten as `y=ax^2+bx+c`, where `x` and `y` are variables and `a`, `b`, and `c` are numbers with `a!=0`. In the case of a single variable, the standard form becomes `ax^2 + bx + c = 0`. (`y=ax^2+bx+c`) to one that is in the vertex form of a quadratic equationWhen the quadratic equation is a quadratic function, the vertex form is `y=a(x-h)^2+k`, where `x` and `y` are variables and `a`, `h`, and `k` are numbers - the vertex of this parabola has the coordinates `(h, k)`. , or `y=a(x-h)^2+k`. In vertex form, the point `(h,k)` will be the vertex, which is either the lowest point of the parabola (if `a` is positive and the parabola opens upward) or the highest point (if `a` is negative and the parabola opens downward).
Here is an example where we use completing the square to convert a quadratic equation in standard form to vertex form:
|
Example |
|||||
|
Problem |
Write the quadratic equation `y=3x^2-12x+1` in vertex form and identify the vertex of the parabola. |
||||
|
`y=3(x^2-4x)+1` |
|
Factor out `3`. |
|||
|
`y+3c=3(x^2-4x+c)+1`
|
|
Remember that when we complete the square, we add a value to the expression. Because of the multiplier, this can get a little confusing, so we are going to prepare to complete the square for `x^2 - 4x` by adding `c` to `x^2 - 4x`, inside the parentheses.
When we add a quantity to one side of the equation, we must also add it to the other side. Because the quantity added, `c`, is inside the parentheses on the right, we are actually adding `3c`. This means when we add the quantity to the left side, we must add `3c`. |
|||
|
`y+3(4)=3(x^2-4x+4)+1`
|
|
Complete the square on `x^2 - 4x + c` by finding the value of `c`. `c=(b/2)^2=((-4)/2)^2=(-2)^2=4` Replace both instances of `c` with this value. |
|||
|
`y+12=3(x-2)^2+1` |
|
Write the completed square as a binomial squared. |
|||
|
`y=3(x-2)^2-11`
|
|
Solve for `y` to get the equation in vertex form, `y=a(x-h)^2+k`.
The coordinates of the vertex are `(h,k)`. |
|||
|
Answer |
The vertex is `(2, -11)`. The vertex form of the equation is `y=3(x-2)^2-11`. |
||||
Notice that the value of the coefficient `a` is the same in both vertex and standard form. We can use this to help explain why the point `(h,k)` is the vertex of the parabola when its equation is written as `y=a(x-h)^2+k`. There are two cases:
`1`) The value of `a` is positive: Then, the smallest value `a(x-h)^2` can have is zero, when `h` is equal to `x`. In that case, `y = k`. For any other value of `x`, `a(x-h)^2` is greater than `0`, so `y` must be greater than `k` because a positive value is added to `k` to get `y`. Therefore, the smallest value of `y` is equal to `k`, and the lowest point of the parabola is `(h, k)`.
`2`) The value of `a` is negative: The same reasoning applies, except that this time `a(x-h)^2` is a negative quantity due to `a` being negative and `(x - h)^2` being positive and the two quantities being multiplied creating a negative quantity. Thus the quantity `a(x-h)^2<=0`, and it takes on its largest value of zero when `x = h`. Therefore, the highest point of the parabola is `(h,k)`.
|
Use completing the square to write the quadratic equation `y=x^2-2x-9` in vertex form and then identify the vertex.
A) `y=(x-1)^2-10`; `(1, -10)`
B) `y=(x+1)^2-10`; `(-1,-10)`
C) `y=(x-3)^2-2`; `(3, -2)`
D) `y=(x-1)^2-10`; `(-1, 10)`
|
Completing the square is used to change a binomial of the form `x^2+bx` to a perfect square trinomial `x^2+bx+(b/2)^2`, which can be factored to `(x+b/2)^2`. When solving quadratic equations, completing the square is used to find the roots of the quadratic equation, but we must be careful to add `(b/2)^2` to both sides of the equation to maintain equality.
Completing the square also helps us convert a quadratic equation into vertex form, `y = a(x - h)^2 + k`. In the vertex form of a quadratic equation, the coordinates of the vertex are given by `(h,k)`.